NOMBRES COMPLEXES

Nombre complexe, Forme algébrique

Définition et notation

On admet l’existence d’un nombre imaginaire noté i tel que i²=-1

On appelle nombre complexe tout nombre de la forme 𝑎 + 𝑖𝑏

𝑜ù 𝑎 ∈ ℝ, 𝑏 ∈ ℝ

L’ensemble des nombres complexes est noté ℂ.

Exemple : 2+3i, Ѵ2-6i.

Propriété :

Tout nombre complexe z s’écrit de façon unique sous la forme 𝑧 = 𝑎 + 𝑖𝑏 ;

La forme 𝑎 + 𝑖𝑏 est appelée forme algébrique du nombre complexe.

· Le nombre réel 𝑎 est appelé la partie réelle du complexe,

On note : 𝑎 = ℛ𝑒(𝑧).

· Le nombre réel 𝑏 est appelé la partie imaginaire du complexe,

On note : 𝑏 = ℐ𝑚(𝑧).

Exemples :

• 𝑧 = 3 − 2𝑖 est un nombre complexe de partie réelle 3 et de partie imaginaire −2.

• 𝑧 = 5𝑖 est un nombre complexe de partie réelle 0 et de partie imaginaire 5 ,

Remarque :

-Un nombre complexe dont la partie réelle est nulle est un nombre complexe imaginaire pur. L’ensemble des nombres complexes imaginaires purs est l’ensemble noté 𝑖ℝ.

Exemple : 𝑧 = 5𝑖 est un complexe imaginaire pur.

-Un nombre complexe dont la partie imaginaire est nulle est un nombre réel.

On a: ℝ ⊂ ℂ 𝑒𝑡 𝑖ℝ ⊂ ℂ.

Le seul nombre complexe à la fois réel et imaginaire pur est le nombre nul 0.

Egalite :

Deux nombres complexes z et z’ sont égaux si et seulement si :

-ils ont la même partie réelle

-ils ont la même partie imaginaire

z=a+ib

z’=a’+ib’

z=z’ => a=a’ et b=b.

Operations dans ℂ

Soient 𝑧 = 𝑎 + 𝑖𝑏 𝑒𝑡 𝑧 ′ = 𝑎 ′ + 𝑖𝑏′ deux nombres complexes donnés.

• 𝑧 + 𝑧 ′ = (𝑎 + 𝑎 ′ ) + 𝑖(𝑏 + 𝑏 ′ ) ;

• 𝑧 × 𝑧 ′ = (𝑎𝑎 ′ − 𝑏𝑏 ′ ) + 𝑖(𝑎𝑏 ′ + 𝑎 ′𝑏).

• Pour tout nombre complexe non nul, (𝑎; 𝑏) ≠ (0; 0) et 1

• Soient 𝑧 𝑒𝑡 𝑧′ deux nombres complexes tels que 𝑧 ≠ 0

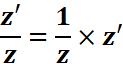
Exemples: Soient deux complexes z=2+3i et z’=4-i

· z+z’=(2+3i) +(4-i)=(2+4) +(3i-i)=6 +2i

· zxz’=(2+3i)( 4-i)=8-2i+12i-3i²=8-2i+12i+3=11+10i.

· .

Oppose d’un nombre complexe

Définition

Soit un nombre complexe 𝑧 tel que 𝑧 = 𝑎 + 𝑖𝑏 𝑜ù 𝑎 ∈ ℝ, 𝑏 ∈ ℝ .

Le nombre complexe opposé de z est le nombre complexe noté -𝑧 tel que :

-z = -𝑎 − 𝑖𝑏.

Exemples :

· z=1+i => -z=-1-i

· z=5-3i => -z=5+3i

Conjugué d’un nombre complexe

Définition

Soit un nombre complexe 𝑧 tel que 𝑧 = 𝑎 + 𝑖𝑏 𝑜ù 𝑎 ∈ ℝ, 𝑏 ∈ ℝ .

Le nombre complexe conjugué de z est le nombre complexe noté 𝑧̅ tel que :

𝑧̅ = 𝑎 − 𝑖𝑏.

Exemples :

· z=1+i => 𝑧̅=1-i

· z=5-3i => 𝑧̅=5+3i

Propriétés

Pour tout nombre complexe z,

z+ 𝑧̅ = 2ℛ𝑒(𝑧).

z- 𝑧̅ = 2i ℐ𝑚(𝑧)..

z x 𝑧̅ = ℛ𝑒(𝑧)² + ℐ𝑚(𝑧)²

Pour tout nombre complexe z,

x ∈ ℝ <= > 𝑧̅ =z

x ∈ iℝ <= > 𝑧̅ = -z

z étant un nombre complexe de forme algébrique a +ib,

z+ 𝑧̅ =2a

z- 𝑧̅ =2b

z x 𝑧̅ = a² +b²

Exemple : écrivons la forme conjuguée de

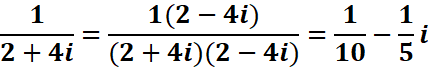
Module d’un nombre complexe

Définition

Le module du nombre complexe

𝑧 = 𝑎 + 𝑖𝑏 est le nombre réel positif noté |𝑧| tel que :

Exemple :

.

Propriétés

Soit (𝑧; 𝑧 ′ ) ∈ ℂ × ℂ, 𝑛 ∈ ℕ :

(i). Si 𝑧 = 𝑎, 𝑎 ∈ 𝐼𝑅 𝑎𝑙𝑜𝑟𝑠 |𝑧| = |𝑎|.

(ii). Si 𝑧 = 𝑖𝑏 , 𝑏 ∈ 𝐼𝑅 𝑎𝑙𝑜𝑟𝑠 |𝑧| = |𝑏|.

(iii). |𝑧 | = |−𝑧| = |𝑧|; |𝑧 × 𝑧′| = |𝑧|.|𝑧′|; |𝑧 ^𝑛| = |𝑧| ^𝑛 .

(iv). Pour 𝑧 ≠ 0, | 𝑧′ 𝑧 | = |𝑧′| |𝑧|.

;

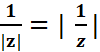(v). |𝑧 + 𝑧′| ≤ |𝑧| + |𝑧′| (inégalité triangulaire).

(vi). |𝑧| ² = 𝑧 × 𝑧 = (ℛ𝑒(𝑧)) ² + (ℐ𝑚(𝑧)) ²

Représentation géométrique d’un nombre complexe

Le plan est muni d’un repère orthonormé direct (𝑂; 𝑢⃗ , 𝑣⃗ ) ; on l’appelle aussi plan complexe.

➢ A tout nombre complexe 𝑧 = a + 𝑖b on associe le point 𝑀(a; b) du plan.

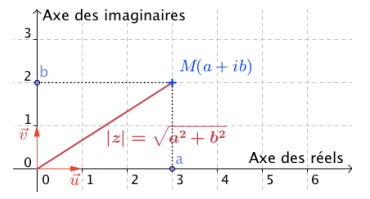
Réciproquement à tout point 𝐴(𝑎; 𝑏) du plan on associe le nombre complexe 𝑧₀ = 𝑎 + 𝑖𝑏. On établit ainsi une bijection entre ℂ 𝑒𝑡 𝒫 (plan). Le nombre complexe 𝑧 = a + 𝑖b est appelé affixe du point 𝑀. On note 𝑧_𝑀.

Le point 𝑀(a; b) est le point image du nombre complexe 𝑧 = a + 𝑖b . On note M(z) .

➢ On associe également à chaque vecteur 𝑤⃗ (𝑎; 𝑏) du plan le nombre complexe 𝑧 = 𝑎 + 𝑖𝑏 appelé affixe du vecteur 𝑤⃗ .

On note 𝑧𝑤⃗= 𝑎 + 𝑏𝑖. Le vecteur 𝑤⃗ (𝑎; 𝑏) est le vecteur image du nombre complexe 𝑎 + 𝑖𝑏.

• (𝑂, 𝑢⃗ ) est appelé l’axe réel ;

• (𝑂, 𝑣⃗ ) est l’axe imaginaire.

Nombre complexe, Forme trigonométrique

Le plan complexe est muni du repère orthonormé direct (𝑂; 𝑢⃗ , 𝑣⃗ ).

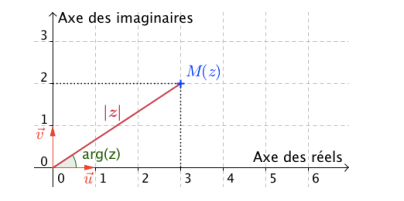
Argument d’un nombre complexe non nul

Définition

Dans le plan complexe muni d’un repère orthonormé direct (𝑂; 𝑢⃗ , 𝑣⃗ ), soit 𝑧 ∈ ℂ ∗ d’image M.

Un argument du nombre complexe z est une mesure en radian de l’angle orienté (⃗𝑢 ̂;𝑂𝑀⃗) .

Remarques :

- Un nombre complexe non nul possède une infinité d'arguments de la forme arg(z) + 2kπ, k ∈ ℤ.

On note :

arg(z) modulo 2π ou arg(z) [2π].

-Tout nombre complexe non nul 𝑧 admet un unique argument appartenant à l’intervalle] −𝜋; 𝜋] appelé argument principal et noté 𝐴𝑟𝑔(𝑧).

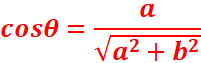
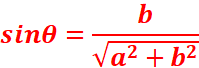
Propriétés

Soient (𝑧; 𝑧 ′ ) ∈ ℂ ∗ × ℂ ∗ , 𝑛 ∈ ℕ :

o arg ( 1/ 𝑧 ) = arg(𝑧 ) = − arg(𝑧) + 2𝑘𝜋, 𝑘 ∈ ℤ

o arg(𝑧 × 𝑧 ′ ) = arg(𝑧) + arg(𝑧 ′ ) + 2𝑘𝜋, 𝑘 ∈ ℤ

o arg(𝑧 ^𝑛) = 𝑛. 𝑎𝑟𝑔(𝑧) + 2𝑘𝜋, 𝑘 ∈ ℤ

o arg ( 𝑧′/ 𝑧 ) = arg(𝑧 ′ ) − arg(𝑧) + 2𝑘𝜋, 𝑘 ∈ ℤ.

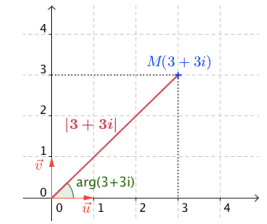
Exemple :

Soit z= 3 + 3i. Alors |z| = 3√2

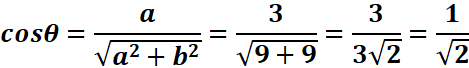
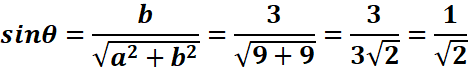
arg (z) = π/4 [2π]

.

Forme trigonométrique d’un nombre complexe

Définition

Soit 𝑧 = 𝑎 + 𝑖𝑏 un nombre complexe non nul ;

𝑟 = |𝑧| 𝑒𝑡 𝜃 un argument de z.

z s’écrit de façon unique sous la forme :

𝑧 = 𝑟(cos𝜃 + 𝑖 sin𝜃).

Cette écriture est appelée la forme trigonométrique du nombre complexe z.

Exemple :

Détermine la forme trigonométrique du nombre complexe 𝒛 = −√𝟑 + 𝒊.

|𝒛| = 𝟐 ;

Soit 𝜑 un argument de 𝑧,

cos(𝜑) = −√3/ 2

sin(𝜑) = 1 /2 on en déduit qu’un argument de z est 5𝜋/ 6

La forme trigonométrique de 𝑧 est :

𝑧 = 2(cos( 5𝜋 /6 ) + 𝑖 sin( 5𝜋/ 6 )).

Remarques :

➢ Pour déterminer la forme trigonométrique d’un nombre complexe on calcule d’abord le module de 𝑧 puis un argument de 𝑧.

➢ La forme trigonométrique d’un complexe est bien indiquée pour déterminer les produits, les quotients ou les puissances d’un nombre complexe.

Forme exponentielle d’un nombre complexe non nul.

Définition

Soit 𝑧 un nombre complexe non nul de module 𝑟 et d’argument 𝜽 .

On appelle forme exponentielle de 𝑧 l’écriture :

𝑧 = 𝑟𝑒 ^𝑖𝜽

Exemple :

2 + 2𝑖 = 2√2𝑒 ^{𝑖 𝜋/ 4} ;

4𝑖 = 4𝑒 ^{𝑖 𝜋/ 2} ;

5 = 5𝑒 ^𝑖0.

Propriété

Soient 𝑧 = 𝑟𝒆 ^𝒊𝜽 𝑒𝑡 𝑧 ′ = 𝑟′𝒆 ^𝒊𝝋 deux nombres complexes non nuls.

(i) 𝑧 ′ = 𝑧 ⇔ 𝑟 ′ = 𝑟 et 𝜑 = 𝜃 + 2𝑘𝜋, 𝑘 ∈ ℤ

(ii) 𝑧 = 𝑟𝒆 ^−𝒊𝜃 ; 𝟏/ 𝒛 = (𝟏 /𝒓 ) 𝒆 ^−𝒊𝜽 .

(iii) 𝑧 ′ × 𝑧 = 𝑟𝑟 ′𝑒 ^{𝑖(𝜃+𝜑)} .

(iv) Pour tout 𝑛 ∈ ℕ, 𝑧 ^𝑛 = 𝑟 ^𝑛𝒆 ^𝒊𝒏𝜽 .

(v) 𝑧′ /𝑧 = 𝑟′ /𝑟 𝒆 ^{𝒊(𝝋−𝜽)}

Remarque :

Ø Soit z un nombre complexe de module r et d’argument θ alors on peut aussi écrire :

z=[r,θ]

Ainsi, soient z=[r.θ] et z’=[r’,θ’]

· z.z’=[r.r’,θ+θ’]

· z/z’=[r/r’,θ-θ’]

· zⁿ=[rⁿ,nθ]

Formule de MOIVRE

Soit 𝜃 ∈ ℝ 𝒆𝒕 pour tout 𝑛 ∈ ℤ .

On a :

(cos𝜃 + 𝑖 sin𝜃) ^𝑛 = cos(𝑛𝜃) + 𝑖 sin(𝑛𝜃).

On appelle cette propriété la formule de Moivre.

Formules d’EULER

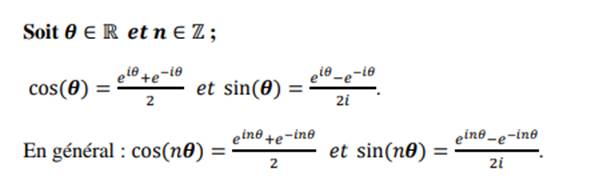
Applications :

Rappels :

-Binôme de Newton : utile pour déterminer les coefficients binomiaux (exemple ci-dessus :1,-3,3,-1)

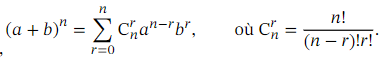
-Triangle de Pascal : utile pour déterminer les coefficients binomiaux

Resolution d’équations dans ℂ

Racines carrées d’un nombre complexe.

Définition

Soit un nombre complexe 𝑧₀, on appelle racine carrée du complexe, 𝑧₀ tout nombre complexe z tel que :

𝑧 ² = 𝑧₀

Méthode :

Soit un nombre complexe z=x+iy

On développe ; z²=( x+iy)²=x²+y² -2ixy

Par identification, on a :

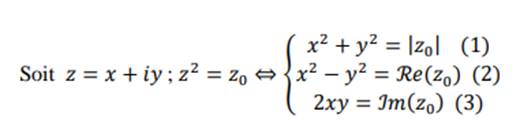
Exemple : Déterminons les racines carrées de :Ѵ3+i

Il suffit de déterminer un complexe z tel que z²= Ѵ3+i

On a :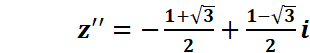

On résout le système et on trouve :

=>

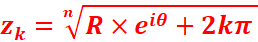
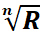
Racine n-ième d’un nombre complexe.

Définition

Soit un nombre complexe z₀ ≠ 0

𝑒𝑡 𝑛 ∈ ℕ 𝒂𝒗𝒆𝒄 𝒏 ≥ 𝟐 .

On appelle racine n-ième de tout nombre complexe 𝑧 tel que :

𝑧 ^𝑛 = z₀

Propriété 1

Soit z₀ = 𝑅𝑒 ^𝑖𝜃 ; les racines n-ième de z₀ sont :

𝑛 𝑎𝑣𝑒𝑐 𝑘 ∈ {0; 1; … ; n-1}.

Propriété 2

Les racines n-ième d’un nombre complexe sont les affixes des sommets d’un polygone régulier de n côtés inscrit dans un cercle de rayon .

Exemple : calculons les racines cubiques de l’unité

Il s’agit de trouver z tel que z³=1

Posons z=cosθ +isinθ

Z³= cos3θ +isin3θ
z³=1 <= > cos3θ +isin3θ=cos0 +isin0 =>

cos3θ=cos0 <= >

Donc:

Equations du second degré.

Propriété

Soit 𝑎, 𝑏 𝑒𝑡 𝑐 sont des nombres complexes avec 𝑎 ≠ 0. Soit ∆= 𝑏 ² − 4𝑎𝑐. Si 𝛿 est une racine carrée de Δ, alors les solutions de l’équation 𝑎𝑧 ² + 𝑏𝑧 + 𝑐 = 0 sont :

Méthode :

-On calcule le discriminant Δ

-on détermine les racines carrées de Δ suivant que Δ est réel ou non

-on calcule les solutions.

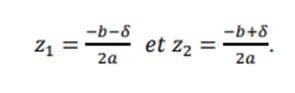
Exemple : soit a résoudre dans C l’équation z²+(2+3i)z-2(1-2i)=0

Δ=b²-4ac=(2+3i)²-4(1)(2(1-2i))=3-4i

Cherchons les racines carrées de 3-4i

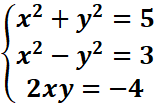
On trouve les deux racines carrées du discriminant : (2-i) et –(2-i)

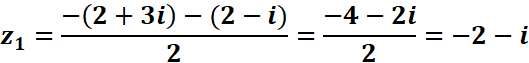
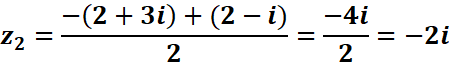
EXERCICES

EXERCICE I : Ecrire sous la forme algébrique les nombres complexes suivants :

a) z₁=(1+3i)-(2+i)

b) z₂=(Ѵ3 +2iѴ2i)-(3+iѴ2)

c) z₃=(Ѵ3 +2iѴ2)(3+iѴ2)

d) z₄=(1+3i)/(2+i)

EXERCICE II:

1. Ecrire sous la forme algébrique les nombres complexes suivants :

a) z₁=(8i-1)/(2-3i)

b) z₂=2i-5/i

c) z₃=(1+i)²/(2-i)²

d) z₄=(4-i)/(2+3i)-i/(3+i)

2. On donne les nombres complexes z₁ et z₂ tels que :

z₁=(5-i)/(3+2i) et z₂=(5+i)/(3-2i)

Calculer : z₁+z₂ ;

z₁-z₂ et conclure.

EXERCICE III:

1.Calculer les modules et les arguments des nombres complexes suivants :

a) z₁=1+i

b) z₂=Ѵ3 +i

c) z₃=1/3 +iѴ3/3

2.En déduire l’ecriture sous forme trigonométrique de z₁, z₂ et z₃

EXERCICE IV:

1.Calculer les modules et les arguments des nombres complexes suivants :

a) z₁=(Ѵ6 -iѴ2)/2

b) z₂=1- i

c) z₃=z₁/z₂

2.Deduire les valeurs exactes de cosπ/12 et sinπ/12

EXERCICE V : On donne les nombres complexes suivants :

z₁=-1-i

z₂=1/2 +iѴ3/2

1.Ecrire z₁/z₂ sous forme algébrique.

2.Ecrire z₁/z₂ sous forme trigonométrique.

3.Deduire de la question précédente les valeurs de cos11π/12 et sin11π/12.

EXERCICE VI

1. Calculer les racines carrées de

i, 3 − 4 i.

2. Résoudre les équations : z ² + z − 1 = 0,

et z²+z+(1-i)/4.

3. Résoudre l’équation

z ² + (i− Ѵ2)z − i Ѵ2 = 0,

puis l’équation Z ⁴ + (i− Ѵ 2)Z ² − i Ѵ2 = 0.

4. Montrer que si P(z) = z ² + bz + c possède pour racines z₁ , z₂ ∈ C alors z₁ + z₂ = −b et z₁ · z₂ = c.

5.Trouver les paires de nombres dont la somme vaut i et le produit 1.

EXERCICE VII : 

1. Mettre les nombres suivants sont la forme exponentielle : 1 + i, Ѵ3 − i, 1/ (Ѵ 3−i) , ( Ѵ3 − i) ²⁰²⁸.

2. Calculer les racines 5-ième de i.

3. Calculer les racines carrées de

Ѵ3 /2 + i /2 de deux façons différentes.

En déduire les valeurs de cos π /12 et sin π /12 .

4. -Développer cos(4θ) ;

-linéariser cos⁵ θ ;

EXERCICE VIII : 

Le plan complexe est muni d’un repère orthonormé direct (O ;⃗𝑢 ,⃗𝑣 ). Dans chaque cas, détermine et construis l’ensemble des points M d’affixe z vérifiant la condition donnée :

a) |𝑧 − 2𝑖| = 3

b) |𝑧 − 1 + 𝑖| = |𝑧 + 1 + 3𝑖|.

c) |2𝑖𝑧 − 3 + 2𝑖| = |𝑧 − 2|.

d) arg(𝑧 − 1 − 𝑖) ≡ 𝜋 6 [2𝜋]

CORRIGES

EXERCICE I : Ecrire sous la forme algébrique les nombres complexes suivants :

a)z₁=(1+3i)-(2+i)=1-2+3i-i=-1+2i

b)z₂=(Ѵ3 +2Ѵ2i)-(3+Ѵ2i)= Ѵ3 -3+2Ѵ2i-Ѵ2i = Ѵ3 -3+Ѵ2i

c)z₃=(Ѵ3 +2iѴ2)(3+iѴ2)=3 Ѵ3+ Ѵ6i+6 Ѵ2i+4i²=(3 Ѵ3 -4)+i(Ѵ6+6 Ѵ2). // on fait i²=-1.

d)z₄=(1+3i)/(2+i)= =(1+3i)(2-i)/(2+i)(2-i)=2+6i-i-3i²/4+2i-2i-i²=5+5i/4-i²=1+i //on multiple le numérateur et le dénominateur par expression conjuguée du dénominateur

EXERCICE II:

1. Ecrire sous la forme algébrique les nombres complexes suivants :

a)z₁=(8i-1)/(2-3i)= (8i-1) (2+3i)=/(2-3i) (2+3i)=(16i+24i²-2-3i)/(4-6i+6i-9i²=-26+13i/13=-2+i

b)z₂=2i-5/i=(2i-5)i/i²=2+5i

c)z₃=(1+i)²/(2-i)²==(1+i) (1+i)/(2-i) (2-i)=2i/3-4i=2i(3+4i)/(3-4i)(3+4i)=-8/25+6i/25

d)z₄=(4-i)/(2+3i)-i/(3+i)= (4-i)(2-3i)/(2+3i)(2-3i)-i(3-i)/(3+i)(3-i)=5-14i/13 –(1+3i)/10=37/130-179i/130

2. On donne les nombres complexes z₁ et z₂ tels que : z₁=(5-i)/(3+2i) et z₂=(5+i)/(3-2i)

z₁+z₂ =(5-i)/(3+2i)+ (5+i)/(3-2i)=2

z₁-z₂=(5-i)/(3+2i)- (5+i)/(3-2i)=-2i

et z₂ est le conjugue de z₁.

EXERCICE III:

1.Calculer les modules et les arguments des nombres complexes suivants :

a)z₁=1+i=>|1+i |=(1²+1²)^1/2=2^1/2=Ѵ2 //le nombre Ѵa peut aussi s’écrire a^1/2

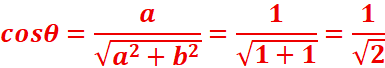
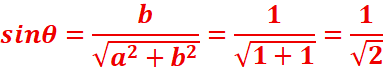
=>θ=π/4

b)z₂=Ѵ3 +i =>| Ѵ3 +i |=(Ѵ3²+1²)^1/2=4^1/2=2

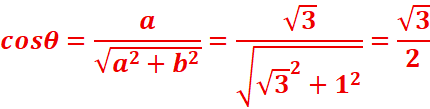
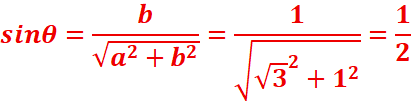
=>θ=π/6

c)z₃=1/3 +iѴ3/3=>|1/3 +iѴ3/3 |=(1/3²+Ѵ3/3²)^1/2=4/9^1/2=2/3

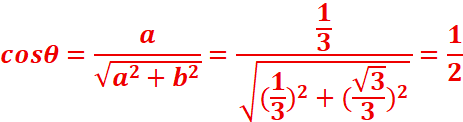
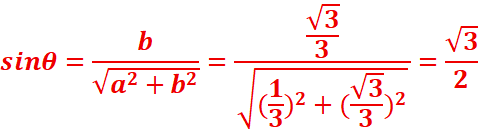
=>θ=π/3

2.En déduire l’ecriture sous forme trigonométrique de z₁, z₂ et z₃

a) |z₁|= Ѵ2 et θ=π/4 => z₁=Ѵ2(cosπ/4 +isinπ/4)

b) |z₂|= 2 et θ=π/6 => z₂=2(cosπ/6 +isinπ/6)

c) |z₃|= 2/3 et θ=π/3 => z₂=2/3(cosπ/3 +isinπ/3)

EXERCICE IV:

1.Calculer les modules et les arguments des nombres complexes suivants :

 a) z₁=(Ѵ6 -iѴ2)/2

|z1|=( Ѵ6/2²+ Ѵ2/2²)^1/2= Ѵ2

cosθ=(Ѵ6/2)/Ѵ2=Ѵ3/2

sinθ=(-Ѵ2/2)/Ѵ2=-1/2=>θ=-π/6

=>z₁=[Ѵ2,-π/6]

b) z₂=1- i

z₂=Ѵ2(1/Ѵ2 -i/Ѵ2)=[Ѵ2,-π/4]

c)z₃=z₁/z₂

z₃=z₁/z₂=[Ѵ2,-π/6]/ [Ѵ2,-π/4]=[1,π/12] // car [r,θ] /[r’,θ’]=[r/r’, θ- θ’]

2.Deduire les valeurs exactes de cosπ/12 et sinπ/12

Sous forme algébrique :

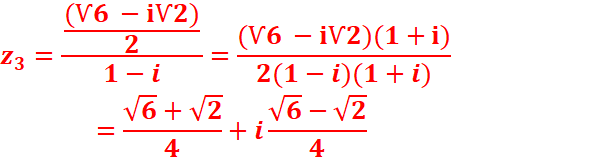
Sous forme trigonométrique :

z₃=[1,π/12]= cosπ/12 +i sinπ/12

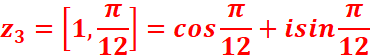
Par identification,

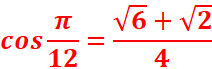
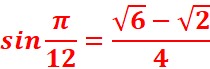
EXERCICE V : On donne les nombres complexes suivants :

Z₁= -1-i

Z₂=1/2 +iѴ3/2

1.Sous forme algébrique.

z₁/z₂ =(-1-i)/( 1/2 +iѴ3/2)=-2(1+i)/(1+iѴ3)=(-1-Ѵ3)/2 +(-1+Ѵ3)i/2

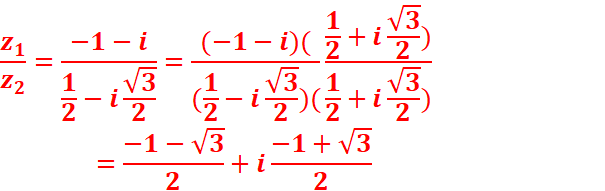
2. Sous forme trigonométrique.

)

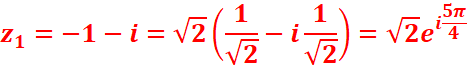
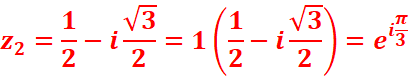
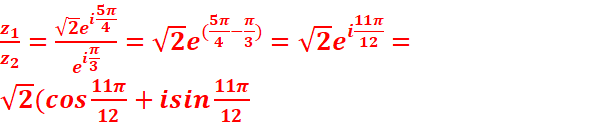3.Deduire de la question précédente les valeurs de cos11π/12 et sin11π/12.

Par identification

)=

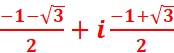
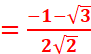
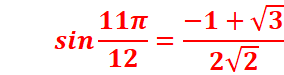
EXERCICE VI

1.

· Racines carrées de −i,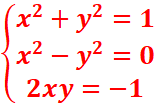

=>

· Racines carrées de 3 − 4 i.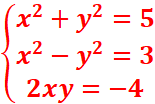

=> 2-i et = -(2-i)

2. Résoudre les équations :

· z ² + z − 1 = 0,

Δ=(1)²-4(1)(-1)=5 // le discriminant donne un réel

z₁=(-1-Ѵ5)/2

z₂=(-1+Ѵ5)/2

· z²+z+(1-i)/4

Δ = i // le discriminant donne un réel, il faut déterminer les racines carrées 𝛿 et - 𝛿

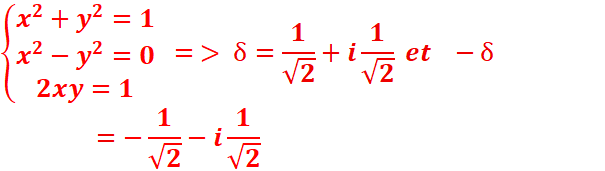
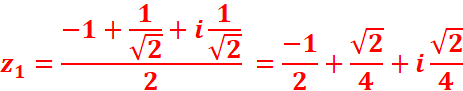
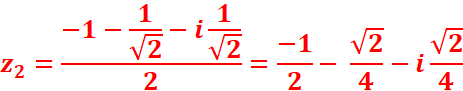
3. Résoudre l’équation :

· z ² + (i− Ѵ2)z − i Ѵ2 = 0,

Δ=(i− Ѵ2)²-4(1)(-iѴ2)=1+2Ѵ2i // le discriminant donne un réel, il faut déterminer les racines carrées 𝛿 et - 𝛿

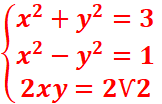=> =Ѵ2 +i et = -Ѵ2-i

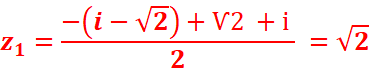
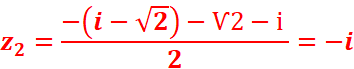
Résoudre l’équation :

· Z ⁴ + (i− Ѵ 2)Z ² − i Ѵ2 = 0.

On pose :Z=z² on retrouve la première équation

Z₁²= -i =>1/Ѵ2 -1/Ѵ2i et -1/Ѵ2 +1/Ѵ2i

Z₂²= Ѵ2 =>- ѴѴ2 et +ѴѴ2

4. Montrer que si P(z) = z ² + bz + c possède pour racines z₁ , z₂ ∈ C alors z₁ + z₂ = −b et z₁ · z₂ = c.

Δ=b²-4ac=b²-4c

z₁=(-b-ѴΔ)/2 et z₂=(-b+ѴΔ)/2

z₁+z₂=(-b-ѴΔ)/2 +(-b+ѴΔ)/2=-2b/2= -b

z₁.z₂=(-b-ѴΔ)/2 x (-b+ѴΔ)/2= c

//en règle générale, lorsqu’une équation de la forme ax²+bx +c=0 admet deux racines x₁ et x₂, la somme des racines S=x₁+x₂ = -b/a et le produit P=x_1.x₂=c/a.

On a donc ax²-Sx +P=0 (ici a=1.)

5.Trouver les paires de nombres dont la somme vaut i et le produit 1.

S=b=i et P=c=1 => ax²-Sx +P=0 <= > ax²-ix +1=0

Δ=b²-4c=i²-4(1)=-5=5i² =(iѴ5)²

z₁=(-i-iѴ5)/2

z₂=(-i+iѴ5)/2

EXERCICE VII : 

1. Mettre les nombres suivants sont la forme exponentielle :

1 + i, Ѵ3 − i, 1/( Ѵ 3−i ), ( Ѵ3 − i) ²⁰²⁴.

·

^·

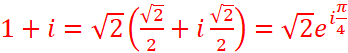
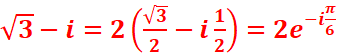
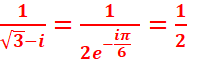· e^iπ/6

^·

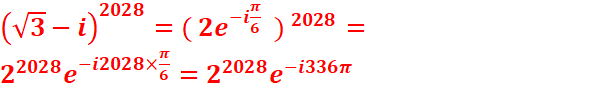
2. Calculer les racines 5-ième de i.

z⁵=i

soit z=r(cosθ+isinθ) =>z⁵=r⁵(cos5θ +sin5θ)

i=cosπ/2 +isinπ/2

r⁵(cos5θ +sin5θ)= cosπ/2 +isinπ/2

=>r=1 et cos5θ= cosπ/2

sin5θ= sinπ/2

5θ=π/2 +2kπ =>θ=π/10 +2kπ/5, k ∈ Z

z_k=cos( π/10 +2kπ/5)+ isin (π/10 +2kπ/5), k ∈ Z

3. Calculer les racines carrées de Ѵ3 /2 + i /2 de deux façons différentes. En déduire les valeurs de cos π /12 et sin π /12 .

1ere Methode:

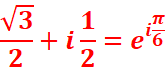
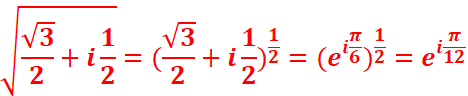
Ѵz=( e^iπ/6)^1/2= e^iπ/12= cos π /12 +isin π /12

2eme Methode:

| Ѵ3 /2 + i /2|=1

z²= Ѵ3 /2 + i /2

=>

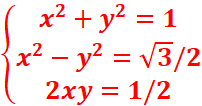(x+y)²-2xy=1 =(x+y)²=1+1/2=3/2=>x+y=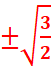

(x-y)(x+y)=Ѵ3/2 < =>(x-y) =Ѵ3/2 =>x-y=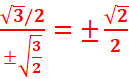

+

+

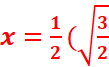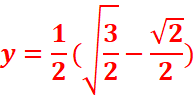
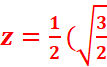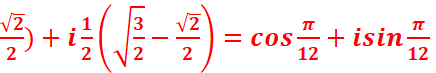
=> cos π /12= +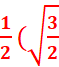

sin π /12=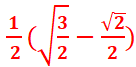

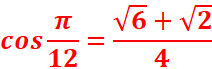
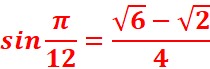
4.

Ø cos4θ+isinθ=(cosθ+sinθ)ⁿ

= cos⁴θ+4cos³θ(isinθ)+6cos²θ(isinθ)²+4cosθ(isinθ)³+(isinθ)⁴

= cos⁴θ+4cos³θ(isinθ)-6cos²θsin²θ-icosθsin³θ+sin⁴θ

= cos⁴θ-6cos²θsin²θ +sin⁴θ+4i(cos³θsinθ- cosθsin³θ)

=> cos4θ= cos⁴θ-6cos²θsin²θ +sin⁴θ

=1-8cos²θsin²θ

=1+8cos2θ+8cos⁴θ

Ø cosθ=1/2(e^iθ+e^iθ)

cos⁵θ=1/2⁵(e^iθ+e^iθ)⁵

=1/2⁵(e^i5θ+ 5e^i4θ e^-iθ+ 10e^i3θ e^-i2θ+ 10e^i2θ e^-i3θ+ 5e^iθ e^-i4θ+ e-^i5θ)

= 1/2^5[(e^i5θ+ e-^i5θ)+5(e^i3θ+ e^-i3θ)+10(e^iθ+ e^-iθ)

=1/2⁴(cos5θ +5cos3θ+10cosθ)

EXERCICE VIII : 

a) |𝑧 − 2𝑖| = 3

L'équation complexe |z – 2i| = 3 représente un ensemble de points M du plan complexe.

Interprétation géométrique :

- z est l’affixe du point M.

- 2i est l’affixe du point A (donc A est à l’origine translatée vers le haut de 2 unités).

- L'équation signifie que la distance entre M et A est constante et vaut 3

b) |𝑧 − 1 + 𝑖| = |𝑧 + 1 + 3𝑖|.

L’équation |z – 1 + i| = |z + 1 + 3i| représente un lieu géométrique.

1. Écriture :

Soit z = x + iy, alors on remplace :

|z – 1 + i| = |z + 1 + 3i|

⇔ |x + iy – 1 + i| = |x + iy + 1 + 3i|

⇔ |(x – 1) + i(y + 1)| = |(x + 1) + i(y + 3)|

2. Modules :

√[(x – 1)² + (y + 1)²] = √[(x + 1)² + (y + 3)²]

On élève les deux membres au carré :

(x – 1)² + (y + 1)² = (x + 1)² + (y + 3)²

Développement :

- (x – 1)² = x² – 2x + 1

- (y + 1)² = y² + 2y + 1

- (x + 1)² = x² + 2x + 1

- (y + 3)² = y² + 6y + 9

Donc :

x² – 2x + 1 + y² + 2y + 1 = x² + 2x + 1 + y² + 6y + 9

Simplification :

- x² et y² se simplifient

- Il reste :

–2x + 2y + 2 = 2x + 6y + 10

Regroupons :

–4x – 4y = 8

⇔ x + y = –2

Résultat :

L’ensemble des points M d’affixe z vérifiant |z – 1 + i| = |z + 1 + 3i| est la droite d'équation x + y = –2

c) |2𝑖𝑧 − 3 + 2𝑖| = |𝑧 − 2|.

On cherche l’ensemble des points M d’affixe z = x + iy vérifiant :

|2i·z – 3 + 2i| = |z – 2|

Étape 1 : Écriture en forme algébrique

Soit z = x + iy, alors :

- 2i·z = 2i(x + iy) = 2i·x – 2·y = –2y + 2ix

- Donc 2i·z – 3 + 2i = –2y – 3 + 2ix + 2i = –2y – 3 + 2i(x + 1)

Donc le module devient :

|2i·z – 3 + 2i| = |–2y – 3 + 2i(x + 1)| = √[(–2y – 3)² + (2x + 2)²]

Et |z – 2| = |(x – 2) + iy| = √[(x – 2)² + y²]

Étape 2 : Égalité des modules

On a :

√[(–2y – 3)² + (2x + 2)²] = √[(x – 2)² + y²]

On élève les deux membres au carré :

(–2y – 3)² + (2x + 2)² = (x – 2)² + y²

Développons chaque côté :

Gauche :

- (–2y – 3)² = 4y² + 12y + 9

- (2x + 2)² = 4x² + 8x + 4

→ Gauche = 4x² + 8x + 4 + 4y² + 12y + 9 = 4x² + 4y² + 8x + 12y + 13

Droite :

- (x – 2)² = x² – 4x + 4

- y²

→ Droite = x² – 4x + 4 + y² = x² + y² – 4x + 4

Étape 3 : Mettre tout à gauche

(4x² + 4y² + 8x + 12y + 13) – (x² + y² – 4x + 4) = 0

→ 3x² + 3y² + 12x + 12y + 9 = 0

On peut simplifier par 3 :

→ x² + y² + 4x + 4y + 3 = 0

Résultat : lieu géométrique

On regroupe :

- x² + 4x + y² + 4y = –3

On complète les carrés :

- x² + 4x = (x + 2)² – 4

- y² + 4y = (y + 2)² – 4

Donc :

(x + 2)² + (y + 2)² – 8 = –3 → (x + 2)² + (y + 2)² = 5

d) arg(𝑧 − 1 − 𝑖) ≡ 𝜋/ 6 [2𝜋]

On cherche l’ensemble des points M d’affixe z tels que :

arg(z − 1 − i) ≡ π/6 [2π]

Interprétation géométrique :

- Cela signifie que le vecteur OM′, avec M′ d’affixe z − (1 + i), forme un angle π/6 avec l’axe réel positif.

- Donc, M est un point tel que le vecteur (z − 1 − i) a un argument égal à π/6 modulo 2π.

Autrement dit, z – (1 + i) est un vecteur de direction π/6.

Conclusion (lieu géométrique) :

L’ensemble des points M d’affixe z est une demi-droite :

- d’origine A(1, 1) (car on a z – 1 – i),

- de direction faisant un angle de π/6 avec l’axe des abscisses, soit pente tan(π/6) = 1/√3.

On peut aussi l’écrire sous forme paramétrique :

z = 1 + i + r·e^{iπ/6} avec r ∈ ℝ⁺*.

Donc, le lieu est la demi-droite partant de A(1, 1) dans la direction π/6

Avez-vous un exercice à proposer ?Cliquez-ici

Merci de votre visite
Laissez un commentaire