: FONCTIONS NUMÉRIQUES

·
Définitions :
ü Soient A et B deux ensembles non vides. On appelle fonction de A vers B, toute correspondance f qui à tout élément de A fait correspondre au plus un élément de B.
Notation : 𝑓 : 𝐴 → 𝐵
. 𝑥 → f(𝑥)
A : est appelé ensemble de départ
B : est appelé ensemble d’arrivé
f(x) est l’image de x par f.
𝑥 est un antécédent de f (𝑥).
Une fonction numérique est une fonction dont l’ensemble de départ et l’ensemble d’arrivé sont des parties de ℝ.

Exemple :
La fonction h définie Sur ℝ par h(x) = (x - 1)² - 4
h(0) = -3,

h(1) = -4.

On dit que -3 est l’image de 0 par h et qu’un antécédent de -3 par h est 0.
Remarque :
Un nombre possède au plus une image.
Un nombre peut posséder plusieurs antécédents.

Domaine ou ensemble de définition de la fonction f

Pour une fonction f donnée, l’ensemble de tous les éléments de A qui ont effectivement une image dans B est appelé domaine ou ensemble de définition de la fonction f, que l’on notera D_f.

Pour trouver l’ensemble de définition d’une fonction, il suffit de trouver la condition d’existence de cette fonction. Pour cela, on examine toutes les contraintes qui apparaissent dans le calcul de l’image de x.

· Si on a , on fixe b

· Si on a , on fixe a

Toute fonction dont l’ensemble de départ coïncide avec son ensemble de définition est appelé application.

Exemple :

Calcul de l’image et de l’antécédent

Soit f une fonction définie de IR vers IR par f(x)=2x+1

· L’image de 3 est f(3)=2(3)+1=7 donc f(3)=7

· L’antécédent de -3 est : 2x+1=-3 < = >2x=-4 =>x=-2 donc f^-1(-3) =-2

Détermination graphique

Graphiquement parlant, le domaine de définition est l’intervalle de l’axe des abscisses dans lequel toute la courbe est circonscrite.
L’image (𝑥) d’une valeur donnée x, se trouve en projetant l’abscisse x sur la courbe parallèlement à l’axe des ordonnées, puis en projetant le point de la courbe obtenu sur l’axe des ordonnées parallèlement à l’axe
des abscisses.
Les antécédents d’un point situé sur l’axe des ordonnées par la courbe, se trouve en effectuant un tracer(au niveau du point) parallèle à l’axe des abscisses, aux niveaux où le tracer touche la courbe, on effectue une projection sur l’axe des abscisses.

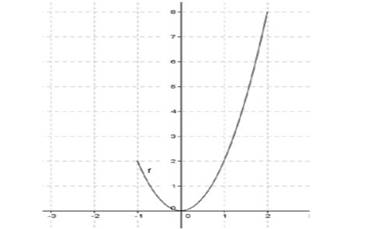
Exemple : Soit f une fonction définie par le graphique ci-contre.

Par lecture graphique, · Domaine de définition : Df= · Image directe : f(1)=2 ;f(1)=3 f()= · Image réciproque f^-1(8)=2 ; f^-1(1)=1 f^-1())=

Variations d’une fonction
Lorsque la courbe d’une fonction va de la gauche vers la droite en descendant sur un intervalle I, on dit que cette fonction est décroissante sur I.

∀ 𝑥₁ ∈ 𝐼, ∀ 𝑥₂ ∈ 𝐼, 𝑥₁< 𝑥₂ =>f(𝑥₁)<f(𝑥₂) ou ≥0

Lorsque la courbe d’une fonction va de la gauche vers la droite en montant sur un intervalle I, on dit que cette fonction est croissante sur I.

∀ 𝑥₁ ∈ 𝐼, ∀ 𝑥₂ ∈ 𝐼, 𝑥₁< 𝑥₂ =>f(𝑥₁)>f(𝑥₂) ou ≤0

La fonction est constante sur I

∀ 𝑥₁ ∈ 𝐼, ∀ 𝑥₂ ∈ 𝐼, 𝑥₁< 𝑥₂ =>f(𝑥₁)=f(𝑥₂) ou =0

Maximum-minimum
Soit f une fonction définie sur un intervalle I :
- 𝑀 ∈ ℝ est un maximum de 𝑓 sur I lorsque : ∀ 𝑥 ∈ 𝐼, f(𝑥) ≤ 𝑀 𝑖𝑙 𝑒𝑥𝑖𝑠𝑡𝑒 𝑥 ∈ 𝐼 𝑡𝑒𝑙 𝑞𝑢𝑒 (𝑥) = 𝑀
- 𝑚 ∈ ℝ est un maximum de 𝑓 sur I lorsque : ∀ 𝑥 ∈ 𝐼, f(𝑥) ≥ 𝑚 𝑖𝑙 𝑒𝑥𝑖𝑠𝑡𝑒 𝑥 ∈ 𝐼 𝑡𝑒𝑙 𝑞𝑢𝑒 (𝑥) = 𝑚

Majorant-minorent

Soit f une fonction définie sur un intervalle I :
- 𝑀 ∈ ℝ est un majorant de 𝑓 sur I lorsque : ∀ 𝑥 ∈ 𝐼, 𝑥 ≤ 𝑀
- 𝑚 ∈ ℝ est un minorant de 𝑓 sur I lorsque : ∀ 𝑥 ∈ 𝐼, 𝑥 ≥ 𝑚

Fonction paire – fonction impaire
Soit f une fonction, D_f son domaine de définition on dit que :
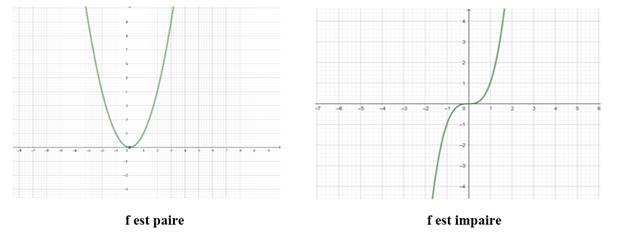
f est paire si pour tout x ϵ D_f tel que -x ϵ D_f on a f(-x) = f(x)
f est impaire si pour tout x ϵ D_f tel que -x ϵ D_f on a f(-x) = - f(x)

Remarque :
La courbe représentative d’une fonction paire est symétrique par rapport à l’axe des ordonnées.
La courbe représentative d’une fonction impaire est symétrique par rapport à l’origine.

. Fonction périodique
soit f une fonction, d’ensemble de définition D_f . Soit T un nombre réel strictement positif. On dit que
f est périodique de période T si pour tout x ϵ D_f tel que x + 𝑇 ϵ Df on a : f(x +T) = f(x)

Eléments de symétrie d’une courbe
centre de symétrie : Soit une f fonction, (C_f) sa courbe représentative. On dit que le point Ι(a,b) est centre de symétrie de (C_f) si pour tout x de Df tel que a - x et a + x appartiennent à D_f on a : f(a – x) + f(a + x) = 2b.ou f(2a – x) + f( x) = 2b

Axe de symétrie : Soit une f fonction, (C_f) sa courbe représentative. On dit que la droite (D) d’équation x = a est un axe de symétrie de (Cf) si pour tout x de Df tel que a - x et a + x appartiennent à D_f , on a : f(a – x) = f(a + x) ou f(2a – x) = f( x)

Fonctions associées à une fonction donnée

Soient f et g deux fonctions de courbes respectives C_f et C_g

1.si g(x)=-f(x) alors C_g est l’image de C_f par symétrie orthogonale par rapport à l’axe des abscisses.

La courbe de la fonction x ↣ - f(x) s’obtient de celle de f en faisant une symétrie par rapport à l’axe des abscisses. Ses variations sont contraires à celles de f.
2. Si g(x)=f(-x) alors C_g est l’image de C_f par symétrie orthogonale par rapport à l’axe des ordonnées.

La courbe de la fonction x ↣ f( - x) s’obtient de celle de f en faisant une symétrie par rapport à l’axe des ordonnées. Ses variations sont contraires à celles de f .

3.Si g(x)=

-Dans la zone du plan où C_f est au-dessus de l’axe des abscisses, alors C_g est confondu à C_f.

- Dans la zone du plan où C_f est en dessous de l’axe des abscisses, alors C_g est l’image de Cf par symétrie orthogonale par rapport à l’axe des abscisses.

4.Si g(x)= ,C_g est la réunion de la courbe C_f située à droite de l’axe des ordonnées et son symétrique par rapport à cet axe.
5. La courbe de la fonction x ↣ f(x - a) s’obtient de celle de f en faisant une translation de vecteur ( a,0) . Ses variations sont identiques à celles de f.
6. La courbe de la fonction x ↣ f(x) + b s’obtient de celle de f en faisant une translation de vecteur ( 0,b). Ses variations sont identiques à celles de f.
7. La courbe de la fonction x ↣ f(x - a) + b s’obtient de celle de f en faisant une translation de vecteur ( a,b). Ses variations sont identiques à celles de f.

EXERCICES

EXERCICE I :

Déterminer les ensembles définition des fonctions suivantes :

a) f(x) =Ѵx

b) f(x)=

c) f(x)=x³ -3

d) f(x)=

e) f(x)=

EXERCICE II:

On donne la fonction f(x)=2x+3

a) Calculer les images de -1 et 5/4 par f

b) Calculer les antécédents de 2 et -5

EXERCICE III:

On donne la fonction f(x)=

a) Donner le domaine de définition de f

b) Donner les images de 1 et 1/3

c) Donner antécédent de 4

EXERCICE IV:

x	-4 -2 2 9
f(x)	1 3 -1 -1

Déterminer :

1. Le domaine de définition

2. Les images de -4 ;-2 ;2 et 9

3. Le maximum et le minimum

4. Le sens des variations dans chaque intervalle.

EXERCICE V:

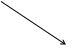
Soit la fonction g représentée par la courbe ci-contre : 1. Déterminer le domaine de définition de g 2. Déterminer les images de : 4 ;5 ; -5 et 6 3. Déterminer l’image directe de : 4. Déterminer les antécédents de : -4 ;1 ;2 et 5 5. Déterminer l’image réciproque de : 6. Résoudre graphiquement les équations g(x) =0 et g(x)= - 6 7. Résoudre graphiquement les équations g(x) 0 et g(x)6 8. Dresser le tableau de variation de g.

EXERCICE VI:

1. a) Montrer que la fonction f(x)= est bornée.

b) Même question pour g(x)=

2. Soit la fonction f(x)=x²

a) Vérifier que la fonction f(x) est croissante sur l’intervalle I=

b) Vérifier que la fonction est décroissante sur l’intervalle I=

c) Montrer que la fonction f(x) est paire

4. Quelle est la parité de la fonction f(x)=

5. Quelle est la parité de la fonction f(x)=

6.On pose f(x)=3 + et Cf sa courbe représentative

Démontrer que le point Ώ (5,3) est centre de symétrie pour Cf

RESOLUTIONS :

EXERCICE I :

a) Ѵx est défini si x

b) est défini si x ⋃

c) x³ -3 est défini dans IR,

d) est défini si 3x+5, =>3x => x, ⋃

e) est défini si x-2=>x,

EXERCICE II:

a) f(-1)=2(-1)+3=1

f(1/4)=2(1/4) +3=7/2

b) 2x+3=2. <=>2x=-1=>x=-1/2=> f^-1(2)=-1/2

2x+3=-5<=>2x=-8=>x=-8/2=-4=> f^-1(-5)=-4

EXERCICE IV:

x	-4 -2 2 9
f(x)	1 3 -1 -1

1.

2.1 ;-1 ;3 ;-2

3. Un maximum

Un minimum

4. f décroissante

f croissante

f décroissante

EXERCICE V:

Résolution :

1.

2.-0,5 ; 0,5 ; 0 ; 5.

3.

4. -0,8 ; -5 et 5,2 ; 5,5 ; 6.

5.

6. S= et S=

7. S=⋃

8.

x	-5 -3 2 4 6
f(x)	1 -9 0,5 -0,5 5

EXERCICE VI:

1.

a) ∀ 𝑥 ∈IR. x² x²

De même 0 x² =>0 x²+1 donc

Cette fonction est majorée et minorée donc elle est bornée ()

b) g(x)==-

or -1

-1

2 donc g est minoré par 2 et majoré par 3

2. a)f(1)=1 et f(3)=9

1<3 => f(1)< f(3) =>f est une fonction croissante sur I=

b) f(-1)=1 et f(-3)=9

-3<-1 => f(-3)> f(-1) => f est une fonction décroissante sur I=

c)f(-x)=(-x)²=x²=f(x)=> f est une fonction paire

4. f(-x)===–f(x) donc f est impaire.

5. f(-x)===–f(x) donc f est impaire.

NB : une fonction peut être ni paire, ni impaire

6.

1^ère méthode : (utilisation de la formule f(a – x) + f(a + x) = 2b. )

f(a – x) + f(a + x)= f(5 – x) + f(5 + x)=( 3 + )+( 3 + )=6+ +=6=2(3)=2b

2ème méthode : (utilisation de la formule f(2a – x) + f( x) = 2b. )

f(2a – x) + f( x) = 2b= f(10 – x) + f( x) = 2b=(3 + ) +(3 + )=6 -+=.6=2(3)=2b

Avez-vous un exercice a proposer?Cliquez-ici

Merci de votre visite
Laissez un commentaire