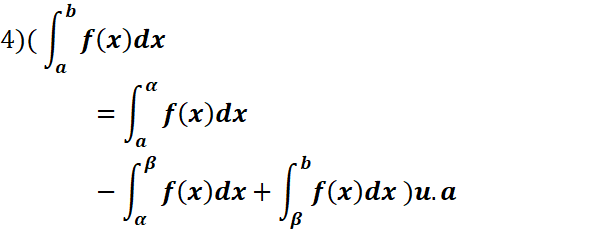CALCUL INTEGRAL
Définition
Soient f une fonction définie sur un
intervalle [a, b] et F une primitive de f. Le
nombre F(b)-F(a) est indépendant de la primitive choisie.
On dit que c’est l’intégrale de la fonction
f, définie entre les valeurs a et b et on note :
F(a)-F(b)=![]()
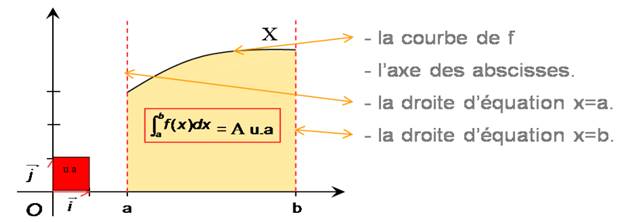
Interprétation graphique de l’intégrale.
Soient f une fonction continue et
positive sur ![]() et (Cf) sa courbe représentative
dans le plan muni d’un repère
orthogonal (O,I,J).
et (Cf) sa courbe représentative
dans le plan muni d’un repère
orthogonal (O,I,J).
Alors :
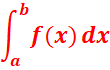
est l’aire, en unité d’aire du domaine
limité par les droites x=a, x=b, la courbe et l’axe des abscisses.
L’unité
d’aire (u.a.) est l’aire du rectangle de dimension
respectives OI et OJ
On appelle valeur
moyenne de f sur [a, b] le nombre réel tel que :
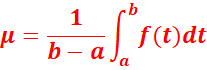
Propriétés des intégrales.
Soient α ,β deux réels, f et g deux
fonctions continues sur un intervalle
de
I de IR, a et b (a ≤ b), deux éléments de I, alors :
· ![]()
· ![]()
· 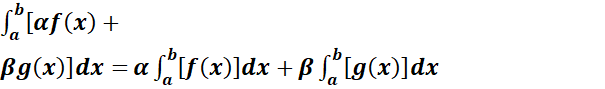
· ![]()
· ![]()
· ![]()
· 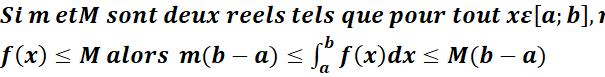
Parité
Soit une fonction continue sur un intervalle K symétrique par rapport à
0.
Pour tout a, élément de K on a :
·
Si f est paire,
![]()
·
Si f est impaire,
![]()
Intégration par parties
Soient u et v deux fonctions dérivables sur un intervalle K telles que
les dérivées u’ et v’ sont continues sur K, a et b
deux éléments de K.
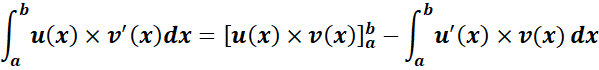
Changement de variable
Pour calculer l’intégrale,
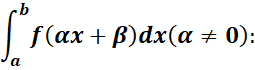
On peut :
·
Faire un changement de variable
![]() , l’intégrale devient :
, l’intégrale devient :
![]()
![]()
·
Utiliser
l’égalité :
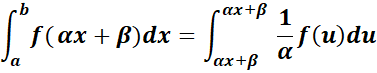
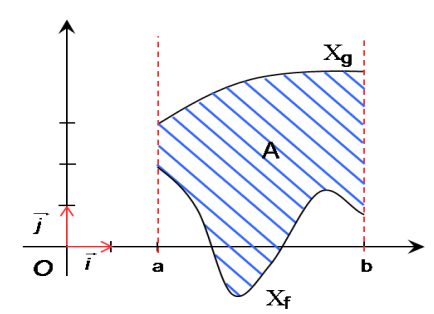
Calcul d’aires
Le plan est muni d’un repère orthonormé
(O,I,J), f et g deux fonctions définies et continues sur un intervalle [a,b ]
|
1) L’unité d’aire (u.a.) est l’aire du rectangle de dimension respectives OI
et OJ
|
|
3) Si
𝑓 est négative sur [𝑎 𝑏] (la courbe
|
|
|
|

Calcul de volume
On considère un cylindre droit dont d’axe (OK),
dont les bases sont contenues dans deux
plans parallèles au plan (OJ) et ayant respectivement pour équation : z=a
et z=b (a<b)
B
est l’aire de la base
V
est le volume
S
application : [a ;b]→IR
z→S(z)dz, S(z) étant l’aire de la section du cylindre
avec un plan parallèle a (OIJ) et du cote z.
On a :
S(z)=B
On obtient :
![]()
Propriété
Le volume V de la
partie d’un solide limitée par les plans Pa et Pb d’équations respectives :
z=a et z=b (a<b)
est déterminé (en u.v) par :

S(t) étant l’aire de la section du solide limitée
par les plans Pt d’équation z=S(t) (a ≤ t ≤ b)
EXERCICES
EXERCICE I : Calculer :
a.![]()
b. 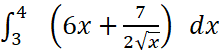
c. ![]()
d. 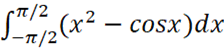
EXERCICE II : Calculer :
a. ![]()
b. ![]()
c. 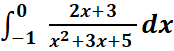
d. 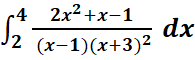
EXERCICE III : Calculer :
a. 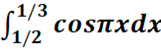
b. ![]()
c. 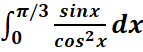
d. ![]()
e. 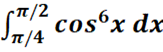
f. ![]()
g. ![]()
EXERCICE IV : Calculer :
a.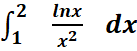
b. ![]()
c. ![]()
d. 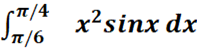
CORRIGES :
EXERCICE I :
Calculer :
a.![]() =
=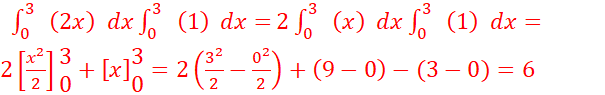 .
.
b.
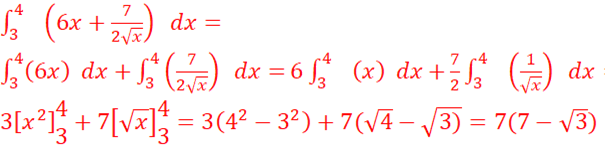
c. ![]()
Pour xε[-2,3],on
a : 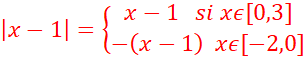
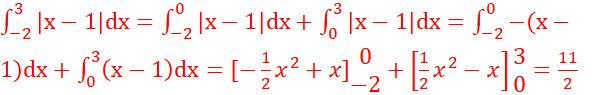 // on utilise ici la
relation de Chasles sur les intégrales.
// on utilise ici la
relation de Chasles sur les intégrales.
d.
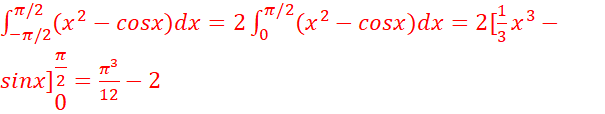 // on utilise ici la parité.
// on utilise ici la parité.
EXERCICE II :
Calculer :
a.
![]() =
=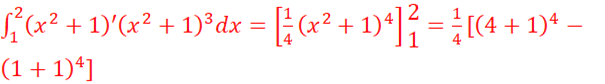 =
=![]()
b.
![]() =
=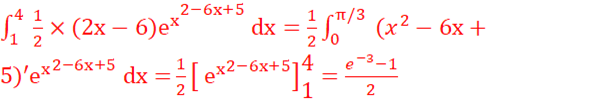
c.
![]() =
=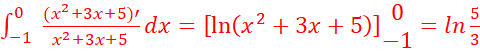 .
.
d.
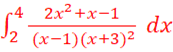 =
=![]() +
+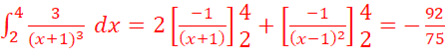
EXERCICE III :
Calculer :
a. 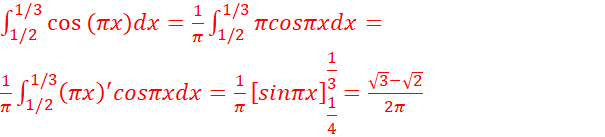
b. 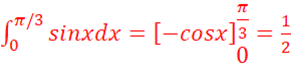
c. 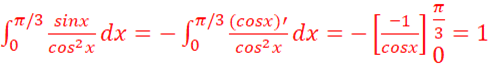
d.
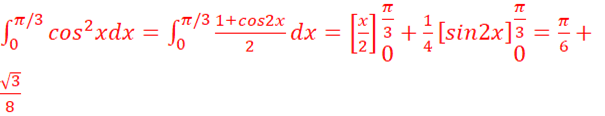
e.
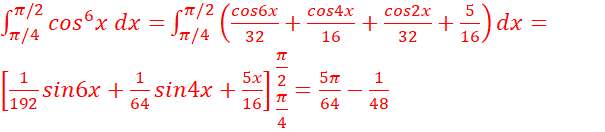
f.
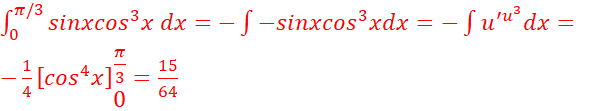
g.
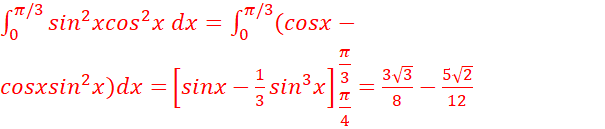
EXERCICE IV :
Calculer
a.![]()
u=lnx u’=1/x
v’=1/x2 v=-1/x
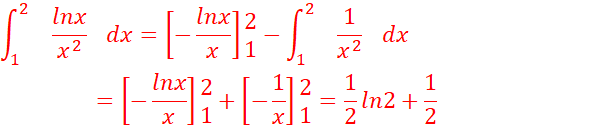
b. ![]()
u=x u’=1
v’=ex v=ex
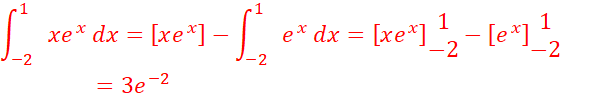
c. ![]()
u=t2 u’=2t
v’=e-t v=-e-t
![]() =
=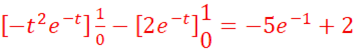
u=t u’=1
v’= e-t v=- e-t
![]() =
=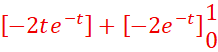
![]() =
=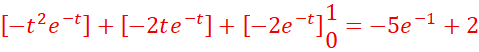
d. 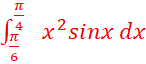
u=x2 u’=2x
v’=sinx
v=-cosx
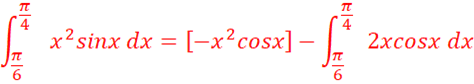
U=x u’=1
V’=cosx v=sinx
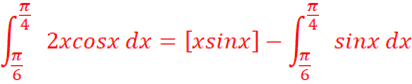
Finalement
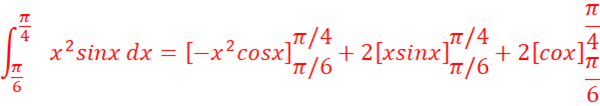
Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire