FONCTIONS EXPONENTIELLES NEPERIENNES

DEFINITIONS

La fonction exponentielle notée exp(x) est la bijection réciproque de la fonction logarithme népérien. Par conséquence, la fonction est définie sur IR par :

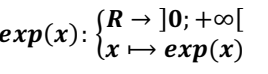
Notations :

.

(e = 2,718 sur la calculatrice)

Conséquence immédiate

Pour tous réels x et y non nuls,

·

·

·

·

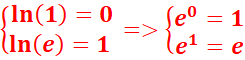
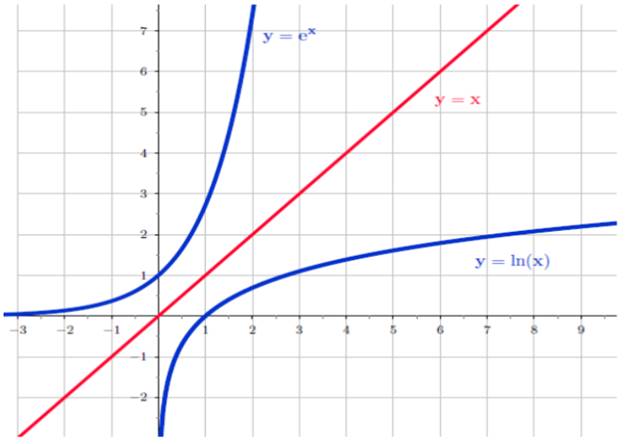
Remarque : Dans un repère orthonormé, les courbes représentatives des fonctions exp(x) et ln(x) sont symétrique par rapport à la première bissectrice. (Tracer la courbe des deux fonctions dans le même repère)

Propriété fondamentale
- Pour tous nombres réels a et b, on a :

e^a+b = e^axe^b

Propriétés

Pour tous reels a et b,

·

·

·

·

·

·

ETUDE DE LA FONCTION EXPONENTIELLE

Domaine de définition :

D_f=IR

Limites

Dérivée de

(e^x)’=e^x

Tableau de variation
La fonction exponentielle est strictement croissante sur IR et on a :

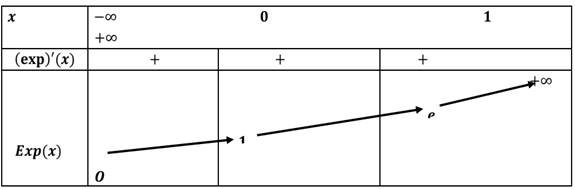
Dérivée de
Si u(x) est une fonction dérivable sur un intervalle K, alors est dérivable sur K et
on a :

(e^u(x))’=u’(x)e^u(x)

Primitive de u’(x)e^u(x)
Si u(x) est une fonction dérivable sur K, alors une primitive de u’(x)e^u(x) sur K est la fonction e^u(x)+k , avec k ϵ IR

FONCTION PUISSANCE

Définition
Soit un réel, on appelle fonction puissance, la fonction notée définie par :

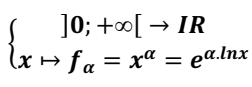
Propriétés (x>0)

·

·

·

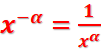
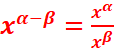
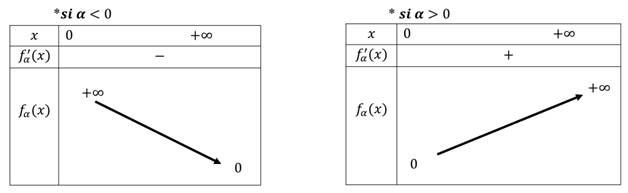
Etude de la fonction puissance (x→x^α )
Domaine de définition

Limites aux bornes du Df

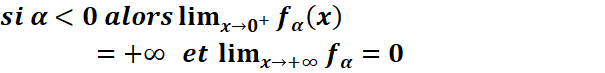
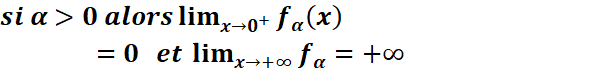
Dérivée et sens de variation

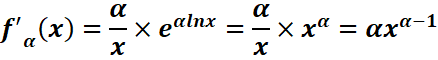
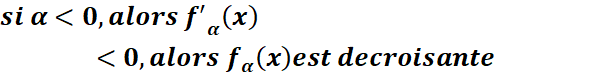
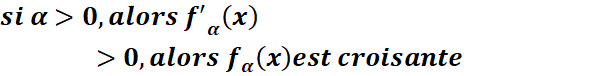
Tableau de variation

EXERCICES

EXERCICE I : Calculez les limites des fonctions suivantes

a.

b.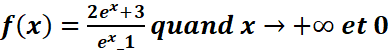

c.

d.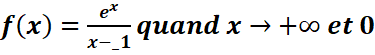

EXERCICE II : Calculez les dérivées des fonctions suivantes

a.

b.

c.

d.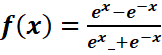

EXERCICE III : Calculez les primitives des fonctions suivantes

a. .

b. .

c. .

EXERCICE IV : Résoudre :

a.

b.

c.

d.

EXERCICE V : Résoudre :

a. ln(x+3)=-2

b. ln(x+3)<-2

c.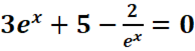

d.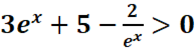

EXERCICE VI :

a) Résoudre dans R, l’équation (E) 

X² - 4X +3 =0.

b) En déduire l’ensemble des solutions de l’équation (E’) :

e^2x – 4e^x + 3=0.

CORRIGES

EXERCICE I : Calculez les limites des fonctions suivantes

a.

b.

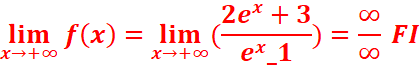
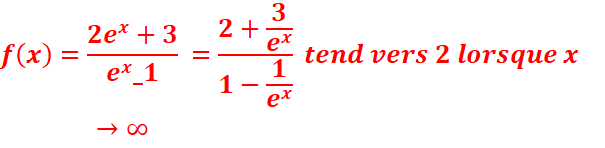
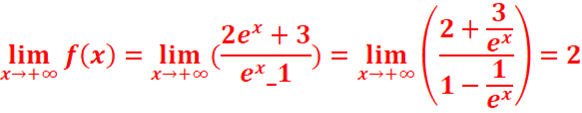
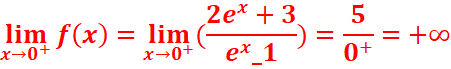
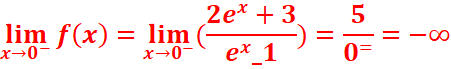
c.

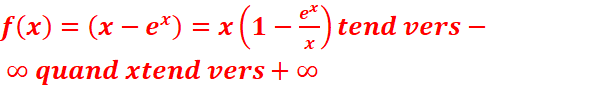//car

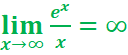
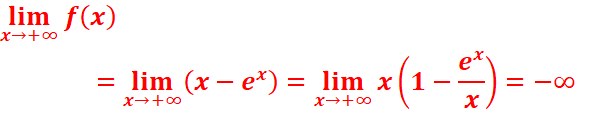
d.

=

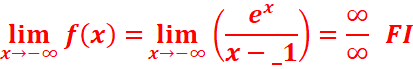
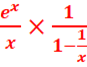
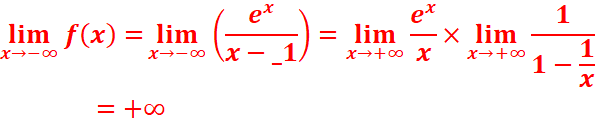
EXERCICE II : Calculez les dérivées des fonctions suivantes

a.

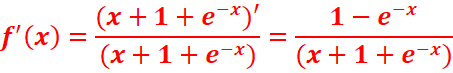
b.

c.

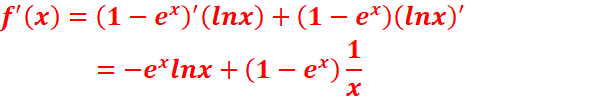
d.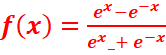

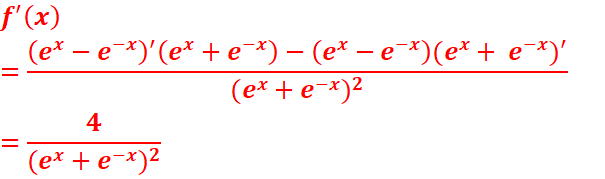
EXERCICE III : Calculez les primitives des fonctions suivantes

a. =-x-3 e^-3x+7=-(-3x+7)’ e^-3x+7=- u’(x)e^u(x)

F(x) =-e^-3x+7 +k, kεIR

b. =(sinx)’ = u’(x)e^u(x)

F(x)=

c. =x (2x+2) = u’(x)e^u(x)

F(x)=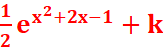

EXERCICE IV : Résoudre :

a. <= > ln. <= > x-3=ln4 =>x=3+ ln4 =>S={3+ ln4 }

b. <= >ln <= > x-3<ln4=>x<3+ ln4 =>S=]-∞,3+ ln4[

c. impossible //la fonction exponentielle est positive

d. impossible //la fonction exponentielle est positive

EXERCICE V : Résoudre :

a. ln(x+3)=-2 <=> e^ln(x+3) =e^-2<=>x+3=e^{-2 =}>x= e^{-2 -}3 => S={ e^-2-3 }

b. ln(x+3)<-2 S=]-∞, e^-2 -3[

c.<=>3e^xe^x+5e^x-2=0<=>3e^2x+5e^x-2=0

On pose X=e^x =>3X²+5X-2=0

Δ=b²-4ac=25-4(3)(-2)=49

X₁=(-5-7)/6=-1

X₂=(-5+7)/6=1/3

X=e^x=-6 impossible

X=e^x=1/3 =>x=ln1/3 =>S={-ln3}

d. >0 <=>3e^2x+5e^x-2>0

S=]∞,-ln3[∪]-ln3,+∞[

EXERCICE VI :

a) Résoudre dans R, l’équation (E) 

X² - 4X +3 =0.

Δ=b²-4ac=16-4(1)(3)=4

X1=(4-2)/2=1

X2=(4+2)/2=3

b) En déduire l’ensemble des solutions de l’équation (E’) :

e^2x – 4e^x + 3=0.

En posant X=e^x on retrouve X² - 4X +3 =0

X=e^x =1=>x=ln1=0

X=e^x =3=>x=ln3

Avez-vous un exercice à proposer ? Cliquez-ici

Merci de votre visite
Laissez un commentaire