INEQUATIONS DU PREMIER DEGRÉ
Définition
Une inéquation
de premier degré dans IR est une inégalité entre deux polynômes du
premier degré ou alors entre un polynôme de premier degré et 0.
Résoudre dans IR une inéquation de premier degré c’est déterminer l’ensemble de
tous les nombres qui vérifient cette inéquation. Cet ensemble est appelé ensemble
solution noté S et est très souvent un intervalle ou une réunion
d’intervalles.
Inéquation du type ax+b < cx+d
Pour résoudre ces types d’équations, on renvoi les termes en x d’un côté
de l’inégalité (de préférence du celui de gauche) et les termes constants de
l’autre côté.
Exemple : Résoudre dans IR
2x+5< x +3
<=>2x-x<3-5
<=> x< - 3
=> S=]←,-3[
Rappel
:
·
Lorsqu’on multiplie ou divise les deux membres d’une inégalité par
un nombre réel négatif non nul, l’inégalité change de sens.
·
Lorsqu’on multiplie ou divise les
deux membres d’une inégalité par un nombre réel positif non nul, l’inégalité
ne change pas de sens.
Exemple :
résolvons les inégalités
suivantes :
·
5x+3<2x-6
< = >5x-2x<-6-3
< = >3x<-9
=>x<-3
·
x+3≥+5x
< = >x-5x≥-3
< = >-4x≥-3 =>x≤3/4
·
-x-2>3x
< = >-x-3x>2
< = >-x-3x>2
< =>-4x>2
=>x>-1/2
Signe du polynôme p(x) = ax + b
La racine (ou le zéro) du polynôme du
premier degré ax + b est –
b/a
. La règle de signe de ce polynôme est
donnée par le tableau de signe ci-après
|
x |
-∞. – b/a. +∞ |
|
ax + b |
signe contraire de a. 0 signe de a |
Exemple : Résoudre -2x + 3<0
Etude du
signe de -2x + 3
La racine
est 3/2
|
x |
-∞. 3/2 +∞ |
|
-2x +
3 |
+ 0 - |
S= ]3/2,+∞[
Inéquation du premier degré de la forme ax+by+c<0
Méthode graphique
Pour représenter l’ensemble des
points dont les coordonnées sont solutions d’une inéquation du 1er degré dans
IR×IR, on procède comme suit :
-On trace la droite dont l’équation est associée à l’inéquation.
- On hachure la partie du plan vérifiant l’inégalité.
Exemple : Résoudre
l’inéquation :2x-y+5>0
Soit la droite(D) d’équation 2x-y+5=0, on
considère le point A (-3,1)
On a : 2(-3) -1+5=-2 et -2 >0 est
faux.
Donc le couple (-3 ;1) n’est pas
solution de l’inéquation2x-y+5>0.
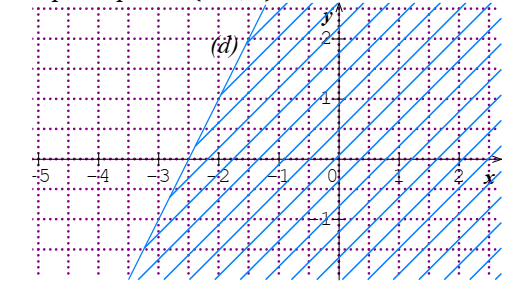
Ainsi l’ensemble des solutions de
l’inéquation 2x-y+5>0 est le demi plan ouvert de frontière(D) ne contenant
pas le point A (-3,1)
EXERCICES
EXERCICE 1 : Résoudre dans. IR les inéquations
suivantes :
1. 5x+3<2x-6
2. 2 ≥
x+2
3.
x+6 ≥3x
4.
-2x+5>x-1
EXERCICE 2 : Résoudre dans. IR les
inéquations suivantes :
1. -3x + 1> x+3
2. 2(3x-1) + 3(x-1) ≥0
3.│x-6│≤3
4.│3x+2│<4
5.│-x+5│≤2
EXERCICE
3
1.Etudier les signes des expressions
suivantes :
a-p(x)=x+2
b-q(x)=(x+2)(x-3)
c-f![]() = (-x+3)/(x-1) avec
x#1
= (-x+3)/(x-1) avec
x#1
d- g(x)= -x+5
2.En déduire les ensembles des solutions des
inéquations : p(x)
< 0 ; q(x)≥0 et f(x)≤0 ![]()
EXERCICE 4 :
1.Un
commerçant dépense 75 F pour fabriquer 150 glaces. Le prix d’une glace est de
2,5 F. Combien doit-il faire de glace pour réaliser un bénéfice supérieur à
76F ?
2.Vous
avez 6000F pour prendre un taxi en course. La course coute 1500F plus 300F par km.
On désigne par x le nombre de km parcourus. Écrire l’inéquation permettant de
calculer a combien de kilomètre pourra vous conduire avec 6000F
EXERCICE
5 :
Résoudre
l’inéquation :2x+3y-1<0
RESOLUTIONS :
EXERCICE 1 : Résoudre dans. IR les inéquations
suivantes :
1. 5x+3<2x-6
<=> 5x-2x<-6-3
<=>3x<-9
<=>x<-9/3
=-3 => S=]←,-3[
2. 2x -1≥ x+2 <=>2x-x ≥
2+1
<=>x![]() =>S=[3 ;⇀[
=>S=[3 ;⇀[
3. x+6 ≥3x <=>x-3x ≥ -6
<=>-2x≥-6
<=>-x≥-3
<=>x≤3
![]() =>S=]
=>S=]![]()
4.-2x+5 > x-1 <=>-2x-x>-1-5
<=>-3x>-6
<=>x<3 => S=]←,3[
EXERCICE
2 : Résoudre dans. IR les inéquations suivantes :
1. -3x + 1>
x+3 <=>-3x-x>3-1
<=>-4x>2 =>x<-1/2 et S=]←,-1/2[
2. 2(3x-1) + 3(x-1)≥0
<=> 6x-2 +3x-3≥0
<=>9x≥5 =>x≥5/9 et S= S=[5/9,→[
3.│x-6│≤3 <=><=>-3![]()
<=>-3+6![]()
<=>3![]() =>S=[3 ;9]
=>S=[3 ;9]
4.│3x+2│<4 <=>-4<3x+2<4
<=>-4-2<3x<4-2
<=>-2<x<2/3 =>S=]-2,2/3[
5.│-x+5│≤2
<=>-2![]()
<=>-2-5![]()
<=>-7![]()
<=>7![]() S=[3 ;7]
S=[3 ;7]
EXERCICE 3
1.Etudier les signes des expressions
suivantes :
a-p(x)=x+2
p(x)=0
=>x=-2
|
x |
|
|
|
x+2 |
- |
+ |
p(x)<0
pour x∈ ]-∞,-2[
p(x)>0
pour x∈]-2,+∞[
b-q(x)=(x+2)(x-3)
q(x)=(x+2)(x-3)=0
=>x=-2 ou x=3
|
x |
|
||
|
x+2 |
- |
+ |
+ |
|
x-3 |
- |
- |
+ |
|
(x+2)(x-3) |
+ |
- |
+ |
q(x)<0 pour x∈]-2,3[
q(x)>0 pour x∈]-∞,-2[U]3,+∞[
c-f(x) =![]() avec x
avec x![]()
|
x |
- |
||
|
x-1 |
- |
+ |
+ |
|
-x+3 |
+ |
+ |
- |
|
|
- |
+ |
- |
f(x)>0 pour
x∈]1,3[]
f(x)<0 pour
x∈]-∞,1[U]3, +∞[
d-
p(x)=-x+5
p(x)=0
=>x=5
|
x |
|
|
|
-x+5 |
+ |
- |
p(x)>0
pour x∈ ]-∞,5[
p(x)<0
pour x∈]5, +∞[
2.En déduire les ensembles des
solutions des inéquations :
p(x)<0 =>S=]-∞, -2[
q(x) ≥0 =>
S=]-∞, -2] U [3, +∞ [
f(x) ≤0 =>]-∞,1] U [3, +∞ [
EXERCICE
4 :
1.Soit x le nombre de glaces réalisées m le bénéfice est la différence
entre ce que l’on gagne (les recettes) et ce que l’on a dépensé pour produire
les glaces :
Bénéfice=recettes – couts=2,50x-75
On veut un bénéfice supérieur à 76F, soit :
2,50x - 75>76
<=>2,50x>76+75=151
=>x >151/2,5 =60,4
2.Soit m le nombre de km parcourus :
1500+200m≤6000<=> 300m≤6000-1500=4500
=>m≤4500/300 =15
EXERCICE
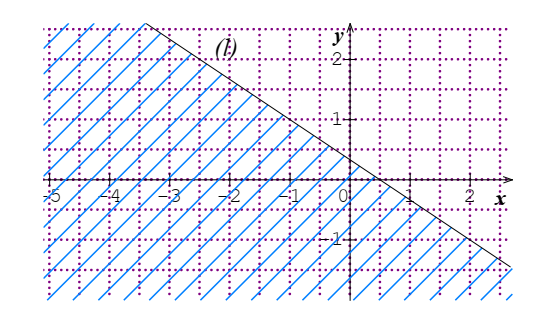
5 :
Soit la droite(L) d’équation
2x+3y-1=0, on considère le point O(0,0)
On a 2(0)+3(0)1-1=-1
et -1<0 est vrai
Donc le couple (0 ;0) est
solution de l’inéquation2x+3y-1<0.
Ainsi l’ensemble des solutions
de l’inéquation 2x+3y-1<0 est le demi plan ouvert de frontière(L) contenant
le point O (0 ;0)
Avez-vous
un exercice à proposer ?Cliquez-ici
Merci de votre visite
Laissez un commentaire