LA LUNETTE ASTRONOMIQUE

Principe

La lunette astronomique est un l’instrument optique destiné à faire voir des objets très éloignés (astres) sous un angle plus grand qu’à l’œil nu comme le microscope, elle se compose de deux systèmes optiques convergents.

- Un objectif : assimilé à une lentille convergente de grand diamètre d’ouverture D et de grande distance focale, qui donne une image réelle agrandie de l’objet.

- Un oculaire, fonctionnant comme une loupe, avec lequel on observe cette image.

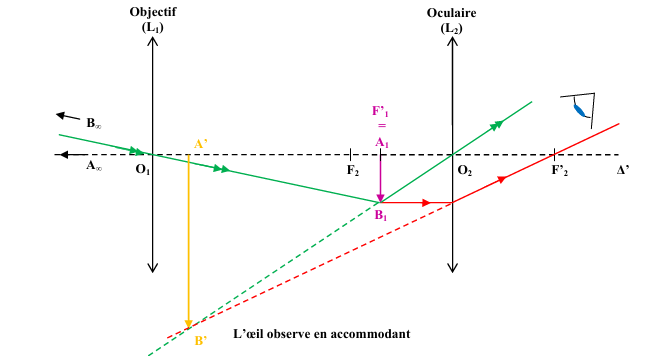
L’image objective d’un astre donné est d’autant plus grande que la distance focale f₁ est plus longue.

Mise au point

La condition idéale pour observer à travers une lunette astronomique est que l’image se forme à l’infini (un œil normal observe les objets éloignés sans se fatiguer). Cette condition est réalisée lorsque F’₁ et F₂ coïncident. La lunette équivaut alors à un système optique sans foyer : elle est dite afocale.

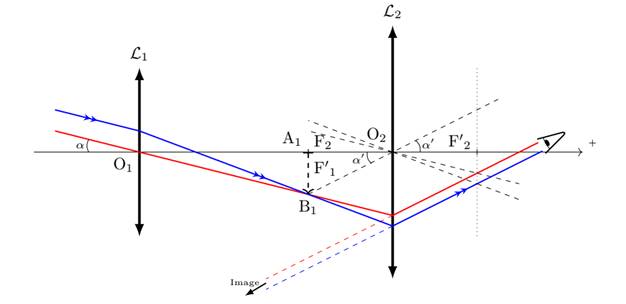
L’objectif et par suite l’image objective A1B1 étant fixe, on met au point en déplaçant l’oculaire par rapport à cette image donc par rapport à l’objectif. La latitude de mise au point (déplacement de l’oculaire L₂) est de l’ordre du cm.

Grossissement

C’est le rapport de l’angle sous lequel on voit l’image dans l’instrument à l’angle sous lequel on voit l’objet à l’œil nu.

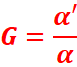
𝜶’ : diamètre apparent de l’image

𝜶 : diamètre apparent de l’objet observé à l’œil nu

G = f₁.f₂ où f₁: distance focale de l’objectif

A₁B₁ = f₁𝜶 ↣ 𝜶 =

P₂ : Puissance de l’oculaire.

G = 𝜶’. = P₂.f₁G = P₂.f₁

Pour une lunette afocale

G = = =>

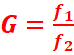
Le grossissement d’une lunette afocale est égal au rapport des distances focales de l’objectif et de l’oculaire. C’est alors une caractéristique de l’instrument seul que l’on appelle grossissement intrinsèque.

Le grossissement est toujours très voisin du grossissement intrinsèque, quel que soit l’œil qui utilise la lunette.

Pouvoir séparateur

La limite de séparation s’exprime, en fraction de minute d’angle, par l’inverse du rayon R de l’objectif exprimé en millimètre.

R en mm

EXERCICES

EXERCICE I:

Dans une lunette astronomique, la distance focale de l’objectif est de 1m. Celle de l’oculaire est de 2 cm et la distance des deux lentilles est de 101,8 cm. A 500m de l’objectif, se trouve un objet de 5 m de hauteur normal à l’axe du système.

1.Calculer la grandeur de l’image objective

2.Calculer la position de l’image objective

3.Calculer la position de l’image finale

4.Calculer la grandeur de l’image finale

EXERCICE II:

Une lunette à un objectif de 2 m de distance focale, un oculaire a une vergence de 50 δ. L’œil de l’observateur est accommodé pour une vision à l’infini

1.Quelle est la distance focale de l’oculaire ?

2.Quelle est la distance des deux lentilles lorsque la lunette est réglée pour une vision à l’infini ?

3.Calculer le grossissement de la lunette

4.De quel angle l’observateur verra-t-il de la lunette deux étoiles dont la distance angulaire est 9.10^-4rad.

EXERCICE III:

Une lunette astronomique est formée de 2 lentilles minces dont les distances focales sont 50 cm et 2 cm

1.Représenter cette lunette pour la vision à l’infini d’un objet très éloigné.

2.Calculer le grossissement de cet appareil

3.Quelle est la distance des deux lentilles ?

EXERCICE IV:

Une lunette afocale donne d’un objet AB situé à l’infini une image A₂B₂ situé à l’infini.

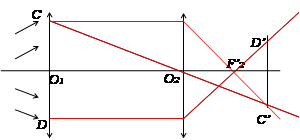
1.Tracer la marche d’un faisceau issu de A et s’appuyant sur les contours CD de l’objectif (A est à l’infini dans la direction de l’axe).

2.Tracer la marche d’un faisceau issu de B et s’appuyant sur les contours CD de l’objectif (B est à l’infini dans la direction faisant un angle 𝜶 avec l’axe.

2.1-Les faisceaux sortant de la lunette ont une partie commune de diamètre C’D’ appelé cercle oculaire. Montrer que le cercle oculaire est l’image de l’objectif à travers l’oculaire.

2.2-Calculer la position du cercle oculaire

2.3-Calculer le diamètre du cercle oculaire

2.4-A quelle distance du Foyer principal image de l’oculaire se trouve le cercle oculaire. Données : f₁ = 2 m ; f₂ = 4 cm ; CD = 8 cm

’

EXERCICE V:

Calculer la latitude de mise au point d’une lunette dont l’oculaire a une puissance de 50 δ.

1- Pour l’œil normal (PP à 25 cm)

2- Pour un œil myope (limite de vision distincte : (1m – 10 cm)

L’œil est placé au Foyer principal image de l’oculaire

EXERCICE VI :

L’objectif et l’oculaire d’une petite lunette astronomique ont pour vergences respectives 1 δ et 50 δ. L’axe de la lune est pointé sur A₁point le plus bas de la lune.

1) Sachant que le diamètre apparent de la lune, observé à l’œil nu est 32 minutes, calculer le diamètre A₁B₁ de l’image réelle donnée par l’objectif.

2) L’œil qui observe à un dm = 22 cm et son centre optique est au foyer image de l’oculaire la lunette est d’abord réglée pour l’infini, puis l’image définitive est ramenée au PP. de combien et dans quel sens faut-il déplacer l’oculaire. En déduire la latitude de mise au point.

CORRIGES

EXERCICE I:

1)𝜶 = = ↣ A₁B₁ = O₁A₁.