L’ŒIL

Description

L’œil est un globe sphérique constituée de :

· La sclérotique ; membrane blanche épaisse et résistante pratiquement indéformable

· La cornée : partie antérieure cette membrane, transparente ;

· La choroïde : deuxième membrane transformant l’œil en chambre noire

· L’Iris : dont la teinte donne aux yeux leur couleur

· La pupille : ouverture du diaphragme, a un diamètre qui peut varier entre 2 et 8 mm environ suivant l’intensité de la lumière reçue par l’œil

· Le cristallin : lentille biconvexe faite d’un corps élastiques transparent

· La rétine : qui tapisse la chambre postérieure, contient les cellules visuelles de l’œil et communique avec le cerveau par les fibres du nerf optique,

L’œil réduit

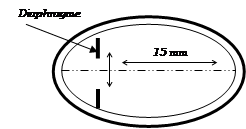
Dans la formation des images, l’ensemble des milieux transparents de l’œil se comporte pratiquement comme une lentille mince convergente (L), plus ou moins diaphragmée ayant ses faces au contact de l’air et dont la distance focale au fond de l’œil est l’ordre de 15 mm.

· L’ensemble formé par la lentille et l’écran sensible que constitue la rétine s’appelle l’œil réduit.

· Un objet n’est vu nettement que si son image se forme sur la rétine.

· Le centre optique O et l’axe principal de la lentille L constituent le centre optique et l’axe optique de l’œil réduit.

Vision à l’infini

Pour un œil normal au repos, l’image d’un objet a l’infini se forme sur la rétine. Le plan focal image de l‘œil au repos coïncide avec la rétine.

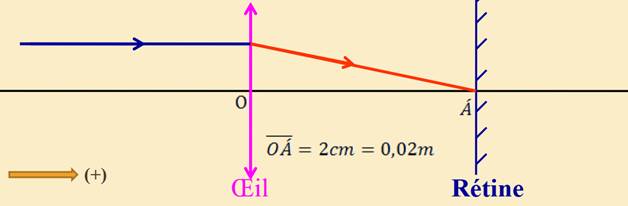
L’accommodation

Pour voir les objets très rapprochés, l’œil doit accommoder car l’image se forme derrière le plan focal image, l’œil diminue sa distance focale pour que cette image soit ramenée au niveau de la rétine.

L’accommodation augmente la vergence de l’œil. Elle est rendue possible grâce à l’élasticité du cristallin ; sous l’action du muscle ciliaire, le cristallin se bombe et, de ce fait, devient plus convergent.

La déformation du cristallin a une limite. Le point de l’axe optique que l’œil voit nettement en accommodant au maximum est appelé le Punctum Proximum de l’œil ; sa distance dm à l’œil est la distance minimale de vision distincte ; placé en deçà de cette distance, tout objet parait flou.

L’effort d’accommodation entraine une fatigue de l’œil et l’on ne saurait observer longtemps un objet placé à la distance minimale de vision distincte. On appelle Punctum remotum PR le point de l’axe optique que l’œil voit nettement lorsqu’il est au repos. C’est la distance maximale de vision distincte Distance recommandée ≃ 25 cm

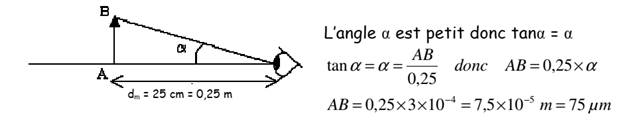
La grandeur de l’image rétinienne

Soit A’B’ l’image rétinienne nette d’un objet AB de diamètre apparent.

On a:

=.

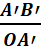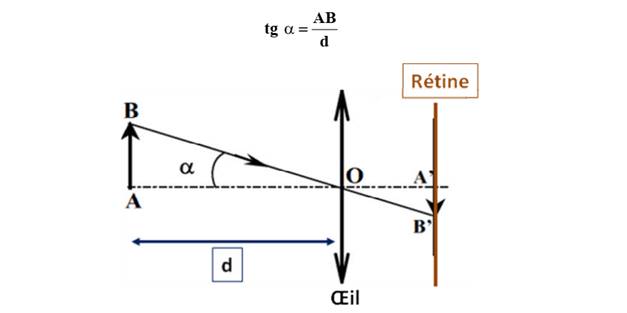
α est généralement petit, on confond α et tanα. Donc on a: tanα =>

A’B’ ≃ OA’.α

en rad

.

Le pouvoir séparateur de l’œil
La rétine est l’écran de l’œil. L’œil ne peut distinguer deux détails d’un objet que
si leur image se forme sur deux cellules différentes de la rétine. Dans des conditions
normales d’éclairement et de contraste, le pouvoir de résolution de l’œil est d’environ 1
minute d’angle (1/60 degré) soit 3×10-4 rad.

La plus petite distance angulaire de deux points séparés par l’œil.

ℰ ≃ (en rad)

a est la distance entre deux bandes consécutives de même nature d’une mire de Foucault

Les principaux défauts de l’œil

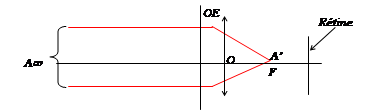
La Myopie

L’œil myope est un œil trop convergent : même lorsqu’il est au repos, son plan focal image F’ est avant la rétine. Il ne peut donc voir nettement les objets éloignés puisque leur image se forme dans ce plan focal.

L’Hypermétropie

L’œil hypermétrope n’est pas assez convergent : au repos son plan focal image F’ est derrière la rétine. Par suite, un œil hypermétrope ne peut voir nettement aucun objet réel sans accommoder. Le PR est virtuel.

On corrige l’hypermétropie en plaçant devant l’œil une lentille convergente

La presbytie

La presbytie est la diminution de la faculté d’accommodation due au vieillissement de l’œil. Elle se traduit par un éloignement du PP.

EXERCICES

EXERCICE I:

On représente très simplement l’œil comme un système constant d’une lentille convergente de centre optique O (le cristallin) et d’un écran (la rétine) la distance lentille-rétine reste constante.

1) Construire l’image d’un objet AB à l’infini dans le cas d’un œil myope, d’un œil normal, d’un œil hypermétrope. Où se situe l’image A’B’ dans chaque cas.

2) Construire très simplement ces mêmes images pour un œil myope et un œil hypermétrope corrigés par une lentille L adéquate.

EXERCICE II :

On considère un œil normal dont la rétine est située à 15 mm en arrière du centre optique de la lentille.

1) Rappeler la définition d’un œil normal.

2) Où se situe le PR de cet œil.

3) En déduire la distance focale de la lentille représentant cet œil et sa vergence quand l’œil est au repos

4) Cet œil permet de voir nettement les objets rapprochés expliquer le phénomène.

5) Trouver la distance focale de cet œil quand l’objet est situé à 2 m

EXERCICE III :

On considère un œil normal d’un individu de 40 ans dont le PP est situé à 25 cm.

1) Que représente le PP

2) La distance cristallin-rétine de cet œil est constante égale à 15 mm. Calculer la vergence quand l’œil observe un objet placé au PP.

EXERCICE IV :

Pour l’œil normal d’un jeune enfant, la distance minimale de vision distincte est de 10 cm. La distance cristallin-rétine de cet œil est constante et égale à 15 mm.

1) Calculer la distance focale et la vergence maximale au PP

2) Calculer la distance focale et la vergence de cet œil au repos

3) Quelle est l’augmentation de la vergence entre le PP et PR ?

EXERCICE V :

Un œil dont le PP se trouve à 36 cm est caractérisé par la distance cristallin-rétine égale à 14,5mm

1) Calculer la distance focale du cristallin et sa vergence maximale

2) Sachant que l’accommodation augmente sa vergence de 6 dioptres, calculer la vergence de la lentille représentant l’œil au repos ainsi que sa distance focale. En déduire le défaut de cet œil.

EXERCICES VI :

Un œil myope à son PR situé à 1 m et son PP à 10 cm.

1) Calculer la vergence de la lentille mince qu’il faut utiliser pour le corriger.

2) Quelle sera alors sa distance minimale de vision distincte.

EXERCICE VII :

Un œil voit sans accommoder les objets situés à 2 m.

1) Quelle est la distance focale de la lentille représentant l’œil sachant que la distance cristallin rétine est égale à 15 mm

2) Quel est le défaut de cet œil ?

3) Quelle est la profondeur en excès de cet œil pour qu’il soit normal ? Justifier votre réponse.

EXERCICES VIII :

Un œil hypermétrope de distance cristallin-rétine est égale à 14 mm possède une vergence égale à 67 dioptries. L’accommodation maximale de cet œil augmente sa vergence de 8 dioptries. Calculer sa distance minimale de vision distincte.

EXERCICE IX :

Un œil myope a son PR situé à 1,25 m.

1) Rappeler la définition du PR

2) Quel est rôle de la lentille correctrice divergente ?

3) En déduire la vergence et la distance focale de cette lentille correctrice.

4) Le PP de cet œil se trouve à 12 cm. Rappeler la définition du PP

5) Où se situe le PP après la correction ? par une lentille divergente ?

EXERCICE X :

Un œil complètement presbyte ne voit nettement que les objets situés à 1 m

1) Calculer la vergence de cet œil sachant que la distance cristallin rétine est égale à 15 mm.

2) Calculer la vergence des lentilles (verres à double foyers) qui lui permette

a) De voir nettement les objets très éloignés

b) De lire un journal à 25 cm de l’œil ?

EXERCICE XI :

Un œil hypermétrope n’est pas assez convergent son PP est à 60 cm au lieu de 25 cm. Par ailleurs s’il observe à l’infini, sans accommoder l’image se forme derrière la rétine, par exemple, à 18 mm derrière le centre optique du cristallin, alors que la rétine est à 16,7 mm de celui-ci.

1) Quelle est la vergence de la lentille correctrice qui permet à cet œil de regarder à l’infini sans accommoder ?

2) Quelle est la distance minimale de vision distincte corrigée par le verre précédent.

EXERCICE XII :

L’œil humain peut distinguer deux points séparés de 0,1 mm à une distance de 25 cm.

a. Calculer l’angle minimal θ que peut distinguer l’œil.

b. Exprimer ce pouvoir séparateur angulaire en radian.

EXERCICE A CARACTERE EXPERIMENTAL

I. Matériel :

-banc d’optique et son dispositif ;

-quatre lentilles (+10 δ, +8 δ, +3 δ, +2 δ) ;

-une lentille divergente (-2 δ)

II. Mode opératoire

Dans tout le TP, nous supposerons que l’objet est à l’infini. Les positions respectives du cristallin et de la rétine demeureront constantes pendant la durée du TP.

1. L’œil normal

Plaçons l’objet AB devant une lentille L1 de vergence C1=+ 10 δ, assimilée au cristallin : il se forme une image nette sur un écran troué, représentant la rétine, le trou étant fermé par un papier calque.

1.1-Faire le schéma du montage

1.2-Déterminer la profondeur de cet œil (distance cristallin-rétine)

2. L’œil myope

2.1- Défaut de cet œil

Remplaçons la lentille L1 par la lentille L2 de vergence C2=+11 δ, représentant le cristallin de l’œil myope.

2.1.1-A partir du matériel donné, comment peut-on obtenir la lentille L2 ?

2.1.2-Dire, après calcul, où se situe l’image formée par rapport à la rétine de l’œil myope ?

2.1.3-Le cristallin de l’œil myope est-il trop convergent ou pas assez convergent ? Justifier par calcul. 0,25pt

2.2 L’œil corrigé

2.2.1-Pour rectifier cette anomalie, on place devant l’œil myope une lentille de vergence C=-2 δ.

Est-ce une lentille convergente ou une lentille divergente ? Justifier la réponse.

2.2.2-Faire le schéma de montage sachant que les lunettes portées par le myope sont des verres de contact (distance œil-lunettes négligeable).

2.2.3-Dire, après calcul, où se situe l’image formée à travers ce système ?

2.2.4-L’œil est-il corrigé avec cette lentille ?

3. L’œil hypermétrope

3.1-Défaut de cet œil

On remplace la lentille L2 par une lentille L3 de vergence C3= +8δ, représentant le cristallin de l’œil hypermétrope.

3.1.1-Dire, après calcul, où se situe l’image formée par rapport à la rétine de l’œil hypermétrope ?

3.1.2- Le cristallin d’un œil hypermétrope est-il trop convergent ou pas assez convergent ?

3.2 L’œil corrigé

3.2.1- Pour corriger le défaut de cet œil, plaçons une lentille de vergence C=+2δ.

Est-ce une lentille convergente ou divergente ? Justifier votre réponse.

3.2.2-Dire, après calcul, où se situe l’image.

3.2.3- L’œil est-il corrigé avec cette lentille ?

CORRIGES

EXERCICE II :

1-Un œil normal est un œil de convergence minimale au repos.

2-Le PR de cet œil est à l’infini

3-Distance focale de la lentille représentant cet œil et sa vergence quand l’œil est au repos.

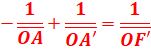
4-Pour voir les objets rapprochés, il y a contraction des muscles ciliaires, ce qui fait augmenter la vergence de l’œil : c’est l’accommodation.

5-

EXERCICE III :

1-Le punctum proximum PP est le point de l’axe optique que l’œil permet de voir nettement en accommodant au maximum.

2-La distance cristallin-rétine de cet œil est constante égale à 15 mm. Calculer la vergence quand l’œil observe un objet placé au PP.

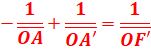
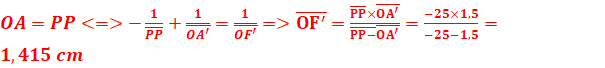
EXERCICE IV :

1)Au PP

= 0,1 = 0,015 m

+ = C = = 76,66

f= = 13,04 mm

2) Au repos, PR = ∞ donc = ∞

+ = C ↔ f = 15 mm et c= = 66,6

3) ΔC= 76,66 – 66,66 = 10

EXERCICE V:

1) Calculons la distance focale du cristallin et sa vergence

= PP = 0,36 m

= 0,0145 m

+ = C = = 71,74

f= = = 13,94 cm

2) C’ = C + 6 = 71,74 + 6 = 77,74

Au repos, sa vergence est : ΔC=Cmax-Cmin =>Cmin=Cmax -ΔC=71,74-6=65,74

f=1/65,74=15,2 cm

3)Cet œil est hypermétrope car l’image d’un objet situé a l’infini se forme derrière la rétine

15,2 cm>14,5 cm

EXERCICES VI :

1) Calculons la vergence de la lentille mince qu’il faut utiliser pour le corriger.

La correction sera faite lorsque l’œil myope pourra voir sans accommoder les objets situés à l’infini c.-à-d. au PR.

- + = C (1)

- + = C +C₁ (2)

(1) – (2)<= > =>C1=

2) Distance minimale de vision distincte.

- + = C (1)

- + = C +C₁ (2)

(1)– (2)<= >

=

EXERCICE VII:

1)

1) = 2 m

= 0,015 m

+ =C = = = =67,16

f= = 14,88 mm

15 > 14,88 ↔ c’est un œil myope

2) 15 – 14,88 = 0,12 mm

EXERCICE VIII:

C = 67

Cmax = 67 + 8 = 75

- + = Cmax

- + = 75 =>dm=28 cm

EXERCICE IX :

1.Le PR est le point le plus éloigné que l’œil peut voir sans accommodation.

2.La lentille correctrice a pour rôle de rejeter le PR a l’infini, de sorte que l’individu puisse voir les objets à l’infini sans accommodation.

3. Vergence et la distance focale de cette lentille correctrice

+ = = C ₍₁₎

Avec la lentille correctrice PR = 10

- + = C + C_{1 (2)}

(2) – (1) : + + = C₁ ] C₁ = 0,8

= 0,8 ] f = -1,25 m

4.Le PP est le point le plus proche que l’œil permet de voir distinctement

5.Position du PP

- + = C ₍₁₎

- + = C + C_{1 (2)}

(2) – 1) : - + = C₁

= C₁+= 0,8+ = 0,8 - 8,33 = -7,53

PP₂ = = -0,133 m

EXERCICE X :

1) Calcul de la vergence de cet œil

C = - = - = 67,67

2 :a)Calcul de la vergence C’ de l’ensemble (lentille + œil).

L’œil voit des objets à l’infini

C’ = = 66,67

Calcul de la vergence C₁ de la lentille correctrice.

C₁ = C’ – C = -1

2,b)Calcul de la vergence C2 de la lentille pour que l’œil voit à 25 cm.

Calcul de la vergence C’’ de l’ensemble (œil + lentille)

C’’ = - avec = - 25 cm

C’’ = 70,67

Calcul de la vergence C₂

C₂ = C’’ – C = 4

70,67 – 67,67 = 3

EXERCICE XI

1) Calcul de la vergence de cet œil dans le cas de la vision à l’infini

C’ = - avec = 18 mm C = 55,55

Calcul de la vergence C’ de l’ensemble (lentille + œil)

C = - avec = 16,7 mm ]

C = 59,88

Calcul de la vergence de la lunette

C1 = C’ – C = 4,33

2) Calcul de la vergence C’’ de cet œil malade dans le cas de la vision minimale

C’’ = - = - = = 61,55

Calcul de la vergence C₂ de l’ensemble (lentille + œil malade).

C₂ = C’’ + C₁ = 65,88

Calcul de la nouvelle distance minimale de vision distincte Dm.

C₂ = - ] = - C₂

= -0,1667 m

Dm = 16,67 cm

EXERCICE XII :

a. θ ≈ séparation / distance = 0,1×10⁻³ / 0,25 = 4×10⁻⁴ rad

b. L’œil peut donc séparer deux objets vus sous un angle θ ≈ 4×10⁻⁴ rad.

EXERCICE A CARACTERE EXPERIMENTAL

1.1-schéma du montage

1.2-Calcul de la profondeur de cet œil (distance cristallin-rétine)

2. L’œil myope

2.1.1-On peut accoler les vergences de 8 δ et de 3 δ.

2.1.2-L’image se forme en avant de la rétine.

2.1.3-Le cristallin de l’œil myope est trop convergent.

2.2 L’œil corrigé

2.2.1-C’est une lentille divergente car c<0.

2.2.2-

2.2.3-La vergence du système est :C’’= C2 +C=11-2=9 δ ≠10 δ

L’image forme a travers ce système est légèrement derrière la rétine (d=0,11m >0,10m distance cristallin-rétine).

2.2.4- Non, l’œil n’est pas corrigé.

3. L’œil hypermétrope

3.1.1- L’image formée est derrière la rétine (d=1/C₃=1/8=0,125)

3.1.2- Le cristallin d’un œil hypermétrope n’est pas assez convergent.

3.2 L’œil corrigé

3.2.1- La lentille est convergente car C>0

3.2.2-L’image se trouve sur la rétine car C3+C=10

3.2.3- Oui, l’œil hypermétrope est corrigé avec cette lentille.

Avez-vous un exercice à proposer ? Cliquez-ici