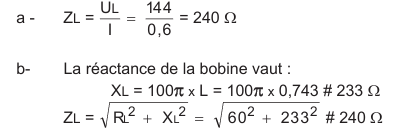OSCILLATEUR
ELECTRIQUE : CIRCUIT RL
GENERALITES
Tout bobinage parcouru par un courant crée un champ
magnétique proportionnel à l’intensité i. Lorsque l’intensité i dépend du temps,
il apparaît aux bornes de la bobine une fém
d’auto-induction (phénomène d’induction). En convention récepteur, cette fém s’écrit (en supposant la bobine idéale, c’est-à-dire
sans résistance) :
L est le coefficient d’auto-induction
de la bobine en henrys(H)
Le rôle d’une bobine d’auto-induction est de
s’opposer à toute modification du courant dans un circuit (loi de Lenz). En
particulier, l’intensité du courant dans une bobine est nécessairement
continue.
L’association en
série d’une bobine et d’un résistor constitue un dipôle
RL.
MISE EN EVIDENCE DES REGIMES TRANSITOIRES
Dispositif expérimental
On réalise un circuit électrique comprenant :
-Un générateur basse fréquence (GBF) délivrant une
tension en créneaux dont les valeurs sont successivement 0V et 6V et dont la
fréquence est réglée à la valeur f=100 Hz
-Une bobine inductive
-Un résistor de résistance R
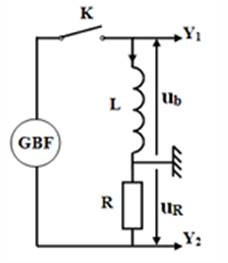
-Lorsque le
générateur délivre une tension umax=E,
l’intensité du courant croit jusqu’à atteindre une valeur maximale constante,
mais cette augmentation est lente.
-Lorsque u=0,
l’intensité du courant décroît jusqu’à s’annuler ; cette extinction de
courant est lente aussi.
-L’établissement
et l’extinction du courant, lentes à atteindre sont conformes à la loi de Lenz.
Energie emmagasinée.
L’énergie Emagn
emmagasinée est donnée par la relation :
L en henrys(H)
I en ampères(A)
Emgn en joules(J)
L’intensité du courant qui traverse une bobine
est une fonction continue du temps.
Equation différentielle d’évolution du circuit
u(t)=uL+uR
Soit encore :
Cette équation différentielle traduit
l’évolution du courant en fonction du temps :
-pendant
l’établissement du courant :
u(t)=E =>
Les solutions sont de la forme :
-pendant l’interruption du courant
u(t)=0 =>
Les solutions sont de la
forme :
ETUDE DU
CIRCUIT RL EN REGIME SINUSOÏDAL
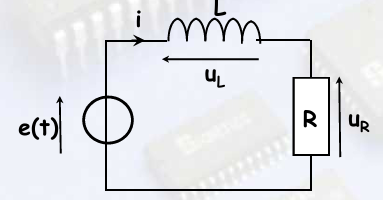
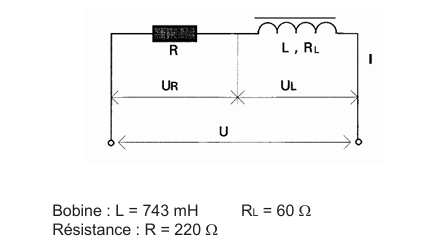
Soit le circuit suivant :
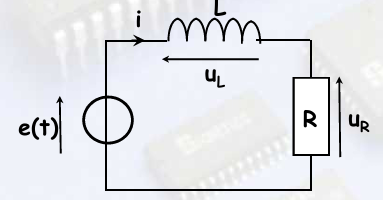
L'ensemble est alimenté par une tension sinusoïdale,
u(t)=e(t)=Umcos(ωt +φ), de valeur efficace
U et de fréquence 50 Hz. Cette tension se décompose en deux tensions partielles
UR et UL. La résistance et la bobine sont en série ; ils
sont donc traversés par le même courant d'intensité efficace I (indiqué sur le
schéma).
IR = IL = I
Tension instantanée aux bornes d’un dipôle RL
Dans un dipôle RL, la tension et l’intensité sont des
fonctions sinusoïdales de même fréquence et présentant un déphasage φ.
Soit i(t)=Imcosωt , alors u(t)=e(t)=Umcos(ωt +φ),
La loi d’additivité des tensions appliquée a la figure ci-dessus donne :
u(t)=e(t) =uL+uR
Soit :
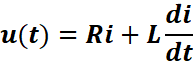
En tenant compte des expressions
ci-dessus :
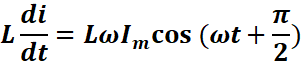
On a :
Construction
de Fresnel
Le courant étant commun aux deux éléments, on le
choisit comme origine des phases.
Le vecteur
, de longueur proportionnelle à la
résistance R, est porté par la direction de I (en phase).
Le vecteur 
, de longueur proportionnelle à la réactance XL=Lω, est perpendiculaire à la
direction de I (déphasé de +π/2).
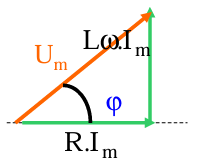
Le vecteur résultant
des deux tensions partielles, représente la tension appliquée U. Cette
résultante est ici l'hypoténuse du triangle rectangle. Sa longueur est
proportionnelle à l'impédance Z.
- La tension aux bornes de la résistance R est en
phase avec le courant et
UR = R x I.
- La tension aux bornes de la bobine L, supposée
parfaite, est déphasée de +π/2 avec le courant (avance de T/4) et
UL = XL
x I=LωI.
- Les deux tensions partielles sont donc en
quadrature.
Caractéristiques du dipôle RL
·
Impédance
D’après le théorème de Pythagore,
=>
·
Déphasage
de la tension appliquée par rapport au courant.
L’angle de déphasage tension/courant est positif et
dépendra du rapport existant entre R et XL à la fréquence de travail
du circuit.
Cet angle est tel que :
Puissance moyenne consommée par le
dipôle RL
·
La tension étant en quadrature avance sur le
courant : φ=π/2 donc cos
φ=0.
·
La puissance moyenne
est P=0 ; une bobine non résistive ne consomme globalement pas
d’énergie : l’énergie emmagasinée au cours d’une alternance est restituée
au cours de l’alternance suivante.
EXERCICES
EXERCICE I :
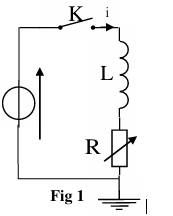
On
réalise le montage représenté dans la figure 1 et qui constitué de :
- un générateur de force électromotrice E=6 V
et de résistance négligeable ;
-
une bobine de coefficient d’inductance L=15 mH et de
résistance négligeable ;
- un conducteur ohmique de résistance R
réglable ;
-
un interrupteur K .
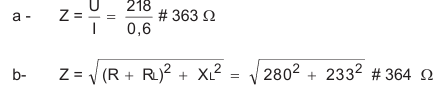
On
règle la résistance R sur une valeur R1 et on ferme l’interrupteur K à un instant t=0
que l’on considère comme origine du temps.
1-
Etablir l’équation différentielle vérifiée par l’intensité du courant i(t).
2-
La solution de l’équation différentielle s’écrit sous la forme :
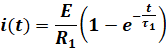
Déterminer
à partir de cette solution l’expression de la constante 
en fonction des paramètres du circuit.
3-
On règle la résistance R sur la valeur R2=2R1
Trouver
l'expression de la nouvelle constante de temps 
en fonction de . En
déduire l’effet de la valeur de R sur l’établissement du courant dans le dipôle
RL.
EXERCICE
II :
On réalise le circuit électrique, schématisé
sur la figure 1, qui comporte :
-
Un générateur de tension de f.e.m.
E =12V ;
-
Une bobine d’inductance L et de résistance négligeable ;
- Deux conducteurs ohmiques de résistance R =
40 W et r=8 Ω ;
- Un interrupteur K.
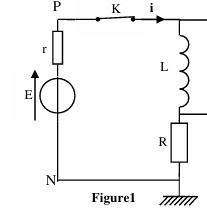
On
ferme l’interrupteur K à l’instant t=0.
1.
Déterminer la valeur de
IP ; l’intensité du courant électrique en régime
permanent.
2.
Etablir l’équation différentielle régissant l’établissement du courant i(t)
dans le circuit.
3. Soit 
,
la solution de cette équation différentielle.
Trouver
les expressions de A et de 
en fonction des
paramètres du circuit.
4. Calculer la valeur de l’inductance L de la
bobine si la constante de temps vaut 3s.
5. Trouver l’énergie E emmagasinée par la
bobine à l’instant t= t /2.
EXERCICE
III :
Un circuit
électrique se compose d'une bobine réelle en série avec une résistance, tel que
représenté ci-dessous :
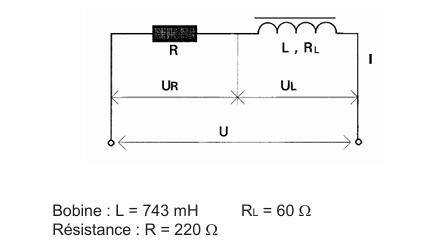
1 - Déterminer, à l'aide de la construction de Fresnel,
quelle tension alternative U (à 50 Hz) il faut appliquer aux bornes du circuit
pour que celui-ci soit parcouru par un courant I de 0,6 A ? Echelle : une
division correspond à 20 V.
2
- Quelle est alors la tension UL aux bornes de la bobine réelle ?
3
- Déduire ou calculer l'impédance ZL de la bobine réelle.
4
- Calculer l'impédance Z du circuit.
EXERCICE
IV :
Un condensateur de capacite C=10μF,
préalablement chargé par une tension continue de valeur UC=10 V est
relié à une bobine de résistance négligeable et d’induction L=0,1 H. A
l’instant initial, la charge du condensateur est Q0 et l’intensité
est nulle.
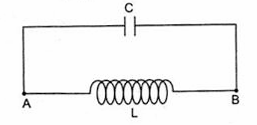
1.Etablir
l’équation différentielle à laquelle obéit la charge q du condensateur.
2.Exprimez
la charge en fonction du temps.
EXERCICE
V :
Situation
problème
En faisant la réception du matériel de physique, un enseignant tombe sur trois
bobines d'inductance non étiquetées. Le listing du matériel reçu indique :
• une (01) bobine d'inductance L=9,0×10−2Het de résistance
interne r=8,3Ω.
• deux (02) bobines d'inductance L=8,86×10−2Het de résistance
interne r=8,9Ω.
Afin de vérifier les caractéristiques et d'étiqueter ces bobines, le
responsable du laboratoire inscrit au hasard un numéro sur chaque bobine (du
numéro 1 au numéro 3), et répartit ses élèves en deux groupes.
|
Groupes |
/Matériel reçu |
|
Groupe 1 - |
bobine numéro 1 ; |
|
Groupe 2 |
bobine numéro 3 ; |
Le
premier groupe réalise le montage de la figure 1 alors que le deuxième groupe
réalise le montage de la figure 2.
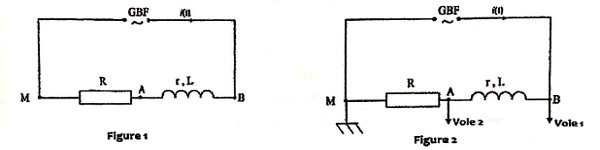
PREMIER
GROUPE
À l'aide des voltmètres, ils mesurent les tensions
efficaces UAM, UBA, UBM et obtiennent les résultats
suivants : UAM=1,41V; UBA=2,06V et UBM=2,83V.
DEUXIÈME GROUPE
Les élèves visualisent à l’oscilloscope la tension
instantanée UBM sur la voie 1 et la tension
instantanée UAM sur la voie 2.
L’oscillogramme obtenu est représenté sur la figure 2.
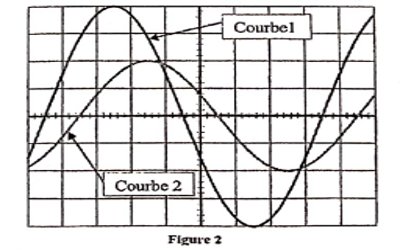Sensibilité verticale:
voie: 1V/div ; voie 2 : 1V/div ; Sensibilité
horizontale : 2,5 ms/div.
1. En utilisant les informations de la première expérience et à l'aide d'une
démarche scientifique, identifie la bobine numéro 1.
2. Utilise les résultats des expériences pour étiqueter les deux autres
bobines.
EXERCICE
V I:
Situation problème
Dans le laboratoire du collège, les élèves de terminale
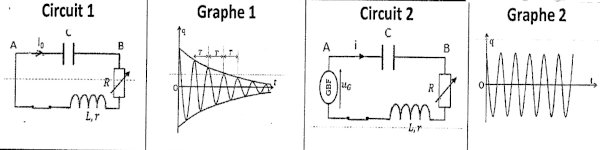
réalisent une expérience. Ils montent un oscillateur (RLC) électrique libre
(circuit 1) et constatent qu'il est le siège des oscillations, amorties (graphe
1).
Ils décident donc d’améliorer le circuit 1 et obtiennent le circuit 2 (résonance d’intensité)
qui est un oscillateur électrique forcé sans amortissement (Graphe 2).
Pour expliquer le phénomène d'amortissement, NGANDO I'un
des élèves estime que celui-ci est dû à la dissipation de l'énergie par effet
Joule ce qui se traduit par (dETdt=−Ri2)
où ET est l’énergie totale du circuit (document 1).
Par ailleurs, les élèves ont des difficultés à choisir le GBF approprié à
partir des GBF mis à leur disposition ( Document 2) pour obtenir un oscillateur
non amorti.
Document 1 : informations utiles V
I - Énergie totale d'un circuit RLC : ET=Econdensateur+Ebobime
Rappel mathématique d(x2)dt=2xdxdt
Document 2 : Caractéristiques des GBF disponibles
A : u=105sin(100πt)
B : u=105sin(200πt)
C : u=105sin(100πt+π2)
D : u=105sin(100πt)
Données :
R=295Ω, r=5Ω et i=0,35sin(100πt)
En exploitant les informations ci-dessus et à I ‘aide d'une démarche
scientifique,
1. Examine la déclaration de NGANDO.
2. Aide les élèves à choisir le GBF. Baccalauréat C 2024
CORRIGES
EXERCICE I :
1- Equation différentielle vérifiée par l’intensité du courant i(t).
-u(t)+uL+uR=0=>u(t)=uL+uR
Soit encore :
Cette équation différentielle
traduit l’évolution du courant en fonction du temps :
u(t)=E => 
2- La solution de l’équation différentielle s’écrit sous la forme :
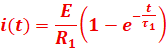
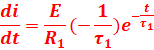
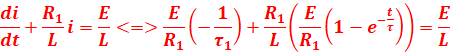
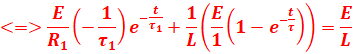
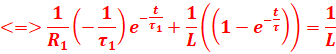
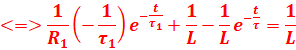
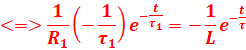
3- R2=2R1
=
Lorsqu’on augmente R, la constante de temps est plus petite et le
temps de rétablissement du courant diminue.
EXERCICE II :
1. L’intensité du courant
électrique en régime permanent est Ip=E/R+r=12/(40+8)=0,25
A.
2. Equation
différentielle vérifiée par l’intensité du courant i(t). R1=R+r
-u(t)+uL+uR=0=>u(t)=uL+uR
Soit encore :
Cette équation différentielle
traduit l’évolution du courant en fonction du temps :
u(t)=E =>
3. Les solutions sont de la
forme :
Par identification,
avec R1=R+r
4. 
5. Trouver l’énergie
E emmagasinée par la bobine à l’instant t= t /2.
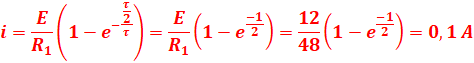
EXERCICE III :
Bobine
: L = 743 mH RL = 60 Ω Résistance : R
= 220 Ω
1 -
Calcul des tensions partielles :
UR
= R x I = 220 x 0,6 = 132 V
URL = RL x I = 60 x
0,6 = 36 V
UXL = 100π x L x
I = 100π x 0,743 x 0,6 = 140 V
Remarque : URL et UXL
ne sont pas accessibles à la mesure
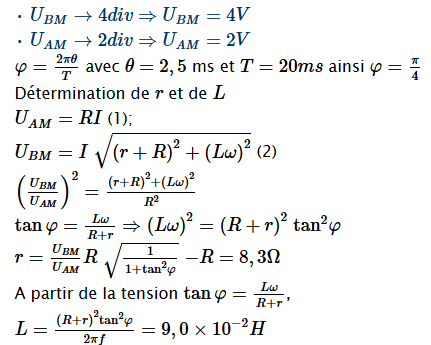
La mesure de U donne environ 11 divisions,
d'où : U = 11 div x 20 V/div. = 220 V
2 -
La mesure de UL donne environ 7,2 divisions, d'où : U L =
7,2 div x 20 V/div. = 144 V
3 -
Calcul de l'impédance ZL de la bobine réelle :
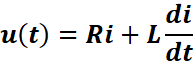
4 -
Calcul de l'impédance Z du circuit :
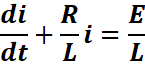
EXERCICE
IV :
Orientons le circuit.
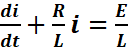
Désignons par q, la charge portée par l’armature du condensateur
reliée au point A, …par uc et uL
respectivement, les tensions aux bornes du condensateur et de la bobine et
fléchées comme l’indique la figure ci-dessus. Avec ces conventions on a les
relations suivantes :
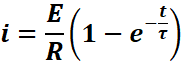
Et comme : uL+uC=0
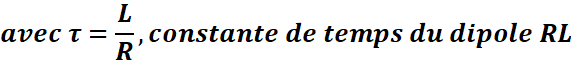
On reconnait l’équation différentielle d’un oscillateur harmonique
de pulsation :
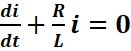
2-La solution est du type :
q(t) = Qm. cos(ωt + φ) Avec les
conditions initiales, à t=0, q=Qm=+Qo et donc: cosφ
=1; soit φ = 0 Et Qo=C.UC=10.10-6.10
= 1,0.10-4 C.
Soit:
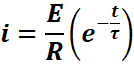
On trace ci-dessous les graphes de q(t) et de sa dérivée i(t)=dq/dt=-Qowsinwt
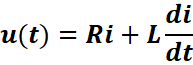
EXERCICE
V :
1.
Il est question de retrouver les caractéristiques de la bobine
numéro 1 afin de l’identifier, pour cela nous allons :
• Écrire les relations entre l’intensité efficace du courant I et les
tensions efficaces UAM, UBA et UBM respectivement.
• Déterminer l’inductance L et la résistance interne r de
la bobine
• Comparer les valeurs obtenues à celles des bobines non étiquetées, puis
conclure
Les valeurs obtenues sont conformes aux caractéristiques de l’une des deux
bobines : la bobine B1
2. Il est question de retrouver les caractéristiques des deux autres bobines
afin de les identifier.
• Identifier les tensions correspondant à la courbe 1 et celle de la courbe 2
• Déterminer a l’aide de l’oscilloscope les tensions
maximales UAM, UBM et le déphasage φ.
• Déterminer l’inductance L et la résistance interne r de
la bobine.
• Comparer les valeurs obtenues à celles des bobines non étiquetés et conclure
Identification des courbes
• Courbes 1 correspond à UBM
• Courbes 2 correspond à UAM
Détermination des tensions maximales et le déphasage.
• UBM→4div ⇒UBM=4V
• UAM→2div ⇒UAM=2V
φ=2πθT avec θ=2,5 ms
et T=20ms ainsi φ=π4
Détermination de r et de L
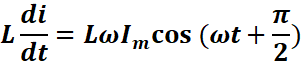
Les valeurs obtenues sont conformes aux caractéristiques de la bobine unique
Bobine 2 : L=8,86×10−2H et r=8,9Ω
Bobine 3 : L=9,0×10−2H et r=8,3Ω
EXERCICE VI:
Situation
problème
Il s'agit de montrer que la variation d'énergie dans l’oscillateur RLC libre
est due à l’effet Joule.
Pour cela il faut :
• Établir l’expression de l'énergie totale emmagasiné dans le circuit ;
• Établir l’expression de la variation de cette énergie cours du temps ;
• Comparer l’expression obtenue à celle de l’énergie dissipée par effet Joule
et conclure.
1.1. Détermination de l’expression de l’énergie totale ET.
ET=Econdensateur+Ebobine
ET=q2/2C+Li2/2
1.2. Détermination de la variation de l’énergie totale en fonction du temps
dET/dt=qCdq/dt+ Lidi/dt=i (qC+Ldi/dt)
Or Ici des mailles ou équation différentielle du circuit RLC :
qC+Ldi/dt+(R+r)i =0⇔qC+Ldi/dt =−(R+r)i
dET/dt=−(R+r)i2
I.3. Comparaison :
L’expression dET/dt=−(R+r)i2 traduit
le même phénomène que dET/dt=−Ri2
Dissipation d’énergie par effet Joule:
Conclusion : NGANDO a raison.