INDUCTION
ELECTROMAGNETIQUE
AUTO-INDUCTION
INDUCTION
ELECTROMAGNETIQUE
L’induction
électromagnétique est un phénomène physique fondamental en électromagnétisme,
découvert par Michael Faraday au début du 19ème siècle. Ce
phénomène décrit la production d’une force électromotrice (FEM) dans un circuit
électrique lorsqu’il est exposé à un champ magnétique variable. En d’autres
termes, un courant électrique peut être induit dans un conducteur lorsqu’il est
soumis à une variation de champ magnétique.
Production d’un courant induit : sa cause et
son sens
Expérience :
Approchons rapidement
un pôle d’aimant de l’extrémité d’un solénoïde fermé sur un milliampèremètre.
Bien que le circuit ne contienne aucun générateur, nous observons une déviation
de l’aiguille du milliampèremètre ; c’est donc qu’un courant parcourt le
circuit : c’est un courant induit.
Interprétation :
Lorsqu’on déplace l’aimant,
le nombre des lignes d’induction qui traversent le solénoïde augmente ; il
y a donc variation du flux d’induction a travers le circuit fermé, cette variation
du flux d’induction est la cause du courant induit, qui s’annule dès que le flux
à travers le circuit cesse.
Soient
deux circuits A et B.
Lorsqu’on fait varier le courant dans le circuit A et on constate une
apparition du courant dans le circuit B
A est le circuit Inducteur
B est le circuit Induit
Conclusion :
Toute variation du flux d’induction a travers un
circuit fermé s’accompagne de la production d’une force électromotrice induite
dans ce circuit Le courant induit apparait dès que commence la variation du
flux ; il disparait dès que cesse cette variation : la cause et l’effet
ont la même durée.
Loi de
Lenz
Si l’extrémité
X du solénoïde est son extrémité nord, elle repousse donc le pôle nord
de l’aimant qui s’approche, tendant à s’opposer à son déplacement.
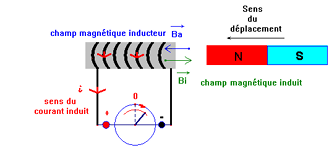
Inversement, si
le pôle nord de l’aimant s’éloigne, le courant induit change de sens, l’extrémité
X du solénoïde devient l’extrémité sud, qui attire le pôle nord de l’aimant
et, par suite tend encore à s’opposer à son déplacement.
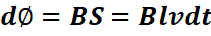
Loi de Lenz : Le sens du courant
induit est tel que par ses effets, il tend à s’opposer à la cause qui lui donne
naissance.
La fem d’induction
L’expression de la fem
d’induction est : 
E en volt
ΔØ en weber
Δt en seconde
La fem instantanée est 
Soit d’après la loi de Lenz :
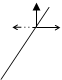
Fem induite dans le cas
d’un conducteur rectiligne fauchant les lignes d’inductions
N
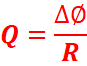
MN = l
M
Intensité du courant
induit :
Quantité
d’électricité :
AUTO
INDUCTION
Définition
L’auto-induction
est le phénomène d’apparition d’une fem lorsqu’un circuit subit la variation de
son propre flux.
Expérience
Lorsque
l'on ferme l'interrupteur K, la lampe L1 s'allume instantanément, alors que la
lampe L2 s'allume avec un retard de quelques secondes.
Interprétation :
Lorsqu’un
courant variable circule dans un circuit comportant une bobine, il crée un
champ magnétique variable. Cette variation s’accompagne de la production d’une
force électromotrice induite appelée force électromotrice d’auto-induction. Le
courant d’auto-induction tend à s’opposer aux variations du courant qui lui
donne naissance. Une bobine tend donc à s’opposer à l’établissement et à
l’annulation du courant.
Auto-inductance
Lorsqu’un
courant quelconque, d’intensité i, parcourt un circuit, il créé dans l’espace
environnant un champ magnétique dont b est en tout point proportionnel à i, il
en résulte, à travers le circuit, un flux d’induction appelé flux propre
proportionnel à b, donc aussi proportionnel à i.
Le coefficient de
proportionnalité L est par définition, l’inductance
du circuit ou auto-inductance.
Unité : le Henry (H)
Fem
d’auto-induction
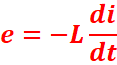
EXERCICES
EXERCICE
I :
Une bobine comprenant N=200 spires,
de rayon moyen égal à 10cm, est placée dans un champ magnétique dont
l’induction magnétique a pour intensité B=0,01T.
1.
Calculer le flux
2.
Quelle est la fem
moyenne induite au cours d’une rotation faisant passer l’angle (
) = θ de zéro à 90 degrés en une 0,5 seconde.
EXERCICE
II :
1.Dans une dynamo, les barres de cuivre qui
constituent les conducteurs dits » actifs » tournent avec une vitesse
v= 20 m/s dans l’entrefer d’un électroaimant ou l’intensité de l’induction
magnétique atteint couramment la valeur B=1 T. Pour l=0,25 m
, calculer dans chaque barre, la fem.
2.On associe 12 conducteurs « actifs » de
résistance totale 60 Ω. Calculer l’intensité du courant délivre par le
générateur ainsi forme.’
EXERCICE III :
Sur un cylindre isolant ayant 10 cm de
diamètre et 3 m de longueur, on enroule régulièrement 1884m de fil de cuivre
dans lequel on fait passer un courant de 1A.
1.On demande de calculer l'induction magnétique B au
centre O de cette longue bobine.
2. On place en O, normalement à l'axe de cette
longue bobine, une petite bobine ayant 1000 spires de 10cm2 de
section. Quelle est la tension induite dans la petite bobine lorsqu'on fait
varier le courant qui traverse la longue bobine de 0 à 1A en 1/100 de seconde,
la variation de ce courant se faisant proportionnellement au temps.
EXERCICE
IV :
Les extrémités d'une
bobine de 1000 spires de 5cm de rayon sont reliées à un galvanomètre. La bobine
est amenée en 0,5 seconde dans un champ uniforme dont les lignes d'induction
sont parallèles à son axe et dont le vecteur d'induction magnétique a pour intensité
B = 0,01 T. Calculer l'intensité moyenne du courant induit sachant que la
résistance du circuit vaut 50Ω.
EXERCICE V :
Une bobine de 200 spires de 10 cm de
rayon, placé dans un champ uniforme d'induction B inconnue, est reliée à un
galvanomètre balistique permettant de mesurer les quantités d'électricité
induites dans la bobine. Sachant que la résistance du circuit ainsi réalisé
vaut 200Ω, et qu'une rotation faisant passer l'angle θ de 0 à 90°
produit une quantité électricité
Q = 3,14.10-4C, calculer l'induction B.
EXERCICE VI :
Un solénoïde de longueur l
comportant N spires de surface S, en admettant que le champ magnétique créé par
le courant qui y circule est uniforme dans la totalité de l’espace intérieure a
ce solénoïde. On donne :N=500 ;l=0,05m ;S=12cm2.
1.
Calculer l’inductance L de ce circuit
2.
On suppose d’autre part que l’intensité du courant i
qui traverse le solénoïde soit une fonction linéaire du temps de la forme :i =10-0,5t
3.
Calculer la fem d’auto-induction
EXERCICE VII :
Situation
problème
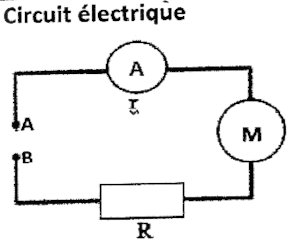
Dans l'atelier de son père, NGUI trouve une meule électrique. Pour contrôler si
son moteur est en bon état, il réalise le montage ci-dessous et fait deux
tests. La résistance r de l’ampèremètre n'est pas négligeable.
Test 1 : il alimente le circuit avec un alternateur constitué d'un rotor
(bobine mobile) de surface S = 130 cm2, comportant 1000 spires de
fil conducteur et plongeant dans un champ magnétique d'intensité B = 0,1 T.
L'angle entre la normale 
à la surface S et le vecteur champ
magnétique →B est fonction du temps tel
que θ=ω.t avec ω=62,8rad.s−1.
Il constate que le moteur ne fonctionne pas normalement.
Le flux magnétique à travers le rotor est alors de la forme : Φ=Φmcosωt.
Test 2 : Il essaye une source de courant continu, il constate que l'intensité
du courant est I = 2 A et que Le moteur fonctionne normalement.
Caractéristiques du moteur
La puissance mécanique
développée est Pm=80W
Le rendement du moteur est η=0,8
Informations utiles:
Tension d'alimentation du circuit pour un bon fonctionnement du moteur
est UAB=80V
Le moteur de la meule est universelle.(fonctionne en courant continu et en
courant alternatif).
Données : R=10Ω et r=5Ω
En exploitant les informations ci-dessus et à l'aide d'une démarche
scientifique,
1. Prononce-toi sur la cause probable du non-fonctionnement du moteur dans le
premier test.
2. Justifie le bon fonctionnement du moteur en évaluant la tension UAB
dans le test (probatoire C et E 2024)
CORRIGES
EXERCICE
I :
1.Si S est la surface d’une spire moyenne,
le flux total initial à travers la bobine a pour valeur, puisque
θ=0 :
Ø =
NBS=200xπx0.12x0,01=0,0628 Wb
2.Pour θ=90, le flux est nul ; la variation de
flux est : Δ Ø=0,0628Wb
Sa durée étant :Δt=0,5s, la valeur de
la fem induite est :
E= Δ Ø/ Δt=0.0628/0,5
= 0,125 V
EXERCICE
II :
1.|e|=Blv=1x0,5x20=10V.
2.
I=E/R=ne/R=12x10/60=2A.
EXERCICE
III :
1.Calcul de l'induction magnétique B au
centre O de cette longue bobine.
N=1884/πd=1884/πx0,1=6000
n=N/l=1500/3=500
B = 4
x 10-7 
= 4 x 10-7 
=
2.
ΔΦ=NBS=1000x2,5.10-3x10.10-4=2,5.10-3
E= ΔΦ/Δt=2,5.10-3 /0,01=0,25
V.
EXERCICE
IV :
ΔΦ=NBS=1000x0,01xπ(0,05)2=0,0785 Wb
I= ΔΦ/R Δt=0,0785/50x0,5=3,14.10-3A
EXERCICE
V :
ΔΦ=NBS
Q= ΔΦ/R= NBS/R
=>B=RQ/NS=200x3,14.10-4/200x3,14x0,01=0,01T
EXERCICES VI :
1. b = 4 x 10-7 
φ=NbS=4 x 10-7 xNxS
φ=LI =>LI= NbS=4 x 10-7 xNxS
=>L=410-7xN2xS/l=410-75002x12.10-4/0,5=0,75.10-3H.
2.i=10-0,5t
φ=Li
e=-L
EXERCICE
IV :
Il s’agit d’évaluer la tension ‘alimentation du circuit en
courant alternatif.
Pour cela, il faut :
Exploiter l’expression du flux magnétique ;
Déterminer la tension efficace délivrée au moteur par l’alternateur ;
Comparer cette tension à celle du fonctionnement normal du moteur et conclure.
1.1 Exploitation de l'expression de la f.é.m. induite.
e=−dφdt=NBSωsinωt
1.2 Détermination de la tension délivrée au moteur
U=emax√2=NBSω√2
AN : U=57,73V
1.3. Comparaison
U≺UAB
Conclusion : la tension délivrée au moteur est insuffisante pour son
fonctionnement normal.
2. Il s’agit d’évaluer la tension d’alimentation du circuit en
courant continu
Pour cela il faut :
• Exprimer et calculer UAB
• conclure
2.1. Appliquer la loi de maille
UAB−UA−UR−UM=0
2.2 Exprimer les tensions
η=Pm/UNI⇒UN=Pm/ηI
UA=rI
UR=RI
2.3 Expression et calcul de UAB
UAB=(R+r)I+Pm/ηI
AN : UAB=80V
2.4 Conclusion
UAB=80V correspond bien à la tension de bon fonctionnement.