LIMITES ET CONTINUITÉ
LIMITES
1- Limite d’une fonction en un point x0
Soit f une fonction numérique définie dans un intervalle I contenant x0.
La limite de f(x) lorsque x tend vers x0 si elle existe
est :
![]()
Exemple :
![]()
![]()
REMARQUE
:
·
Si la limite d’une fonction en un réel x0 existe alors
celle-ci est unique.
· Si
la limite donne un nombre réel différent de de +∞ ou de -∞, elle
est finie.
· Si
la limite donne -∞ ou +∞, elle est infinie.
2-Limite
à gauche –limite à droite de x0.
On
dit qu’une fonction f admet une limite à gauche en x0 égale
à l lorsque :
![]()
On
dit qu’une fonction f admet une limite à droite en x0 égale
à l lorsque :
![]()
.
Exemple :
![]()
![]()
![]() (
(![]() )
)![]()
Le
signe de ![]() dépend du dénominateur
x-1 :
dépend du dénominateur
x-1 :
|
x |
-∞. . . . 1 . . +∞ |
|
|
x-1 |
. - |
. + |
|
signe |
. 0- |
. 0+ |
![]()
![]()
REMARQUE
:
Pour que la limite d’une fonction en un réel existe, il n’est pas nécessaire
que la fonction soit définie en ce réel, mais elle doit être définie au
voisinage de ce réel.
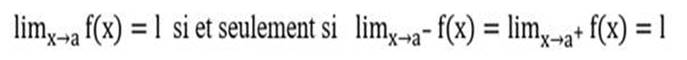
3-Limite des fonctions à l’infini
a-Définition :
Soit
f une fonction définie sur un intervalle I contenant l’infini. On dit que f
admet une limite en + ou – l’infini si l’image de l’infini par f est
définie. On note :
![]()
- La limite d’une fonction polynôme en l’infini est égale à la limite de son
monôme du plus haut degré.
Exemple :![]()
![]()
- La limite d’une fonction rationnelle en l’infini est égale au quotient du
rapport des monômes du plus haut degré au numérateur et au dénominateur.
Exemple :![]()
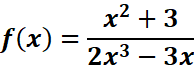
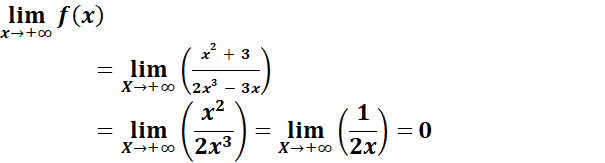
b. Limites à l’infini des fonctions de référence
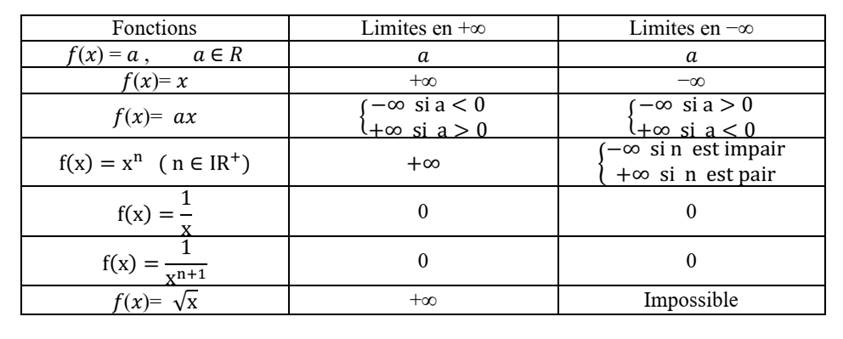
c. Limites à 0 des fonctions de référence
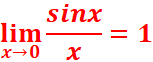
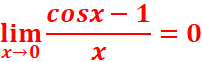
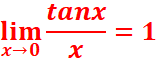
4- Limite et opérations sur les fonctions
Soit f
et g deux fonctions l et l’ deux réels.
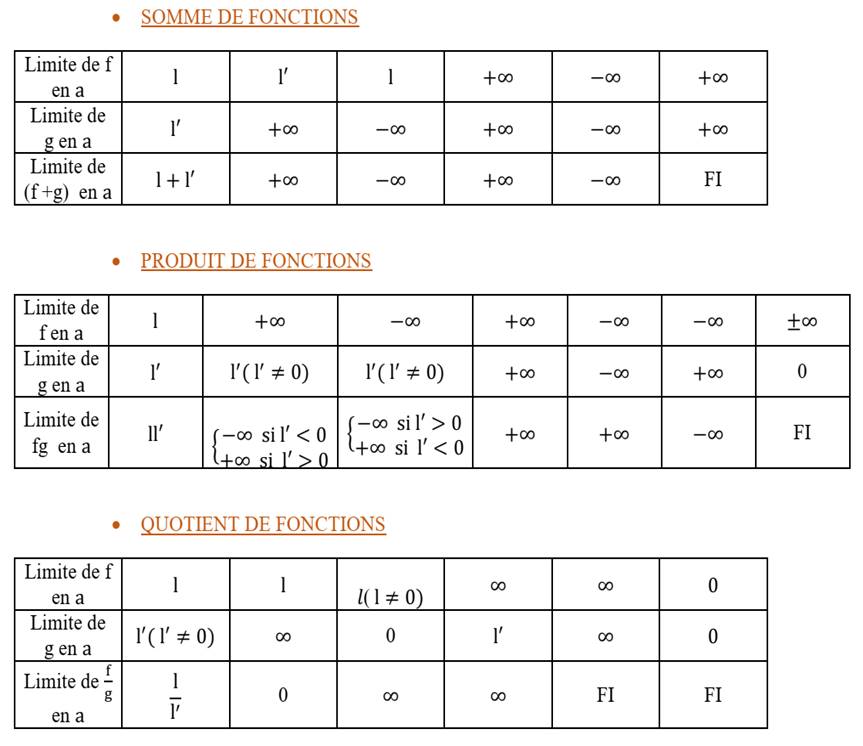

Méthodes pour lever l’indétermination
- Factorisation
Exemple :![]()
![]() Forme
indéterminée
Forme
indéterminée
Pour
lever l’indétermination dans ce cas, on écrit : x-Ѵx =
x(1-Ѵx/x) = x(1-1/Ѵx)
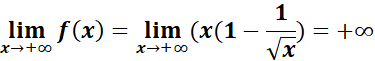
-Utilisation
de l’expression conjuguée
Exemple :![]()
![]() Forme indeterminee
Forme indeterminee
Pour
lever l’indétermination dans ce cas, on écrit :
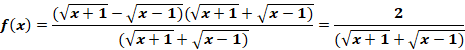
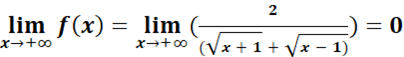
-Utilisation
de l’expression conjuguée et d’une factorisation
Exemple : ![]()
![]()
![]() Forme indeterminee
Forme indeterminee
Pour
lever l’indétermination dans ce cas, on écrit :
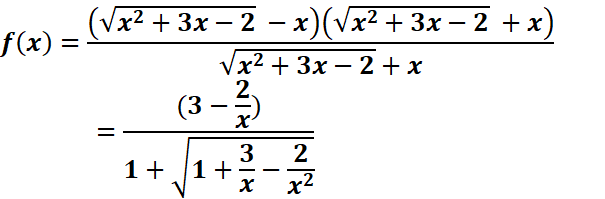
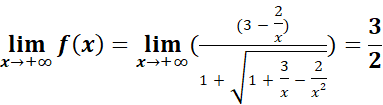
CONTINUITÉ
Définition :
f étant une
fonction définie sur un intervalle ouvert contenant a,
![]()
Continuité à gauche et à droite en un réel

PROPRIÉTÉS
Une fonction est continue en x0 lorsqu’elle est continue
à gauche et à droite de x0.
Exemple :
![]()
![]()
![]() .
.
Continuité sur un intervalle
Une
fonction f est dite continue sur un intervalle K lorsque sa restriction à K est
continue en tout élément de K.
Prolongement par continuité
f est une fonction définie sur son ensemble de
définition Df, a un nombre réel
n’appartenant pas à Df. On suppose que f
admet une limite finie l en a.
alors la fonction g définie par :
 est continue en a.
est continue en a.
Elle
est appelée le prolongement par continuité de f en a.
Exemple : soit la
fonction ![]()
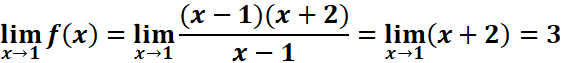
Un
prolongement de f par continuité en x0=1 est :
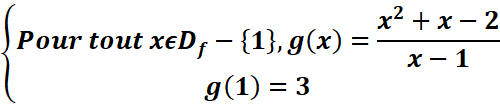
EXERCICES
EXERCICE
I : Calculer
les limites des fonctions suivantes :
1.![]()
2.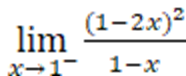
3.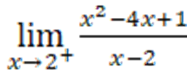
4.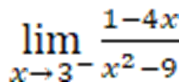
5.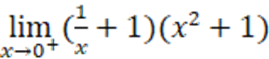
EXERCICE
II : Calculer
les limites des fonctions suivantes :
1.![]()
2.![]()
3.![]()
4.![]()
5.![]()
EXERCICE
III :
1.
Rappeler les limites suivantes :
![]()
2.
Calculer les limites en 0 de chacune des fonctions suivantes :
1.![]()
2.![]()
3.![]()
4.![]()
EXERCICE
IV : Peut-on
prolonger f par continuité en 0 ?
1.![]() Df=
Df=![]()
2. ![]() . Df=
. Df=![]()
3. ![]() . Df=
. Df=![]()
4.Montrer
que la fonction f ci-dessous est continue en x0=0
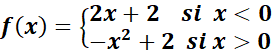
EXERCICE
V :
Peut-on prolonger f par continuité en 1 ?
1. ![]() Df=
Df=![]()
2. ![]() Df=
Df=![]()
CORRIGES :
EXERCICE I :
1. ![]()
2.![]() =
=![]() =
=![]() =+∞
=+∞
3.![]() =
=![]() =
=![]() = -∞
= -∞
4.![]() =
=![]() =
=![]() =+∞
=+∞
5. ![]() =
=![]() =∞.0 FI. Il faut lever indétermination
=∞.0 FI. Il faut lever indétermination
![]()
![]() =
=![]() =
=![]() =+∞
=+∞
EXERCICE II : Calculer les limites des
fonctions suivantes :
1.![]() =
=![]() =
=![]() FI. Il
faut lever l’indétermination.
FI. Il
faut lever l’indétermination.
![]() =
=![]()
![]() =
=![]() .
.![]() =2.1.1=2
=2.1.1=2
2.![]() =
=![]() =
=![]() =FI. Il faut
lever l’indétermination.
=FI. Il faut
lever l’indétermination.
![]() =
=![]() .sinx
.sinx
![]() =
=![]() .
.![]() =
=![]() .=0
.=0
3.![]() =
=![]() =
=![]() =
=![]() FI. Il faut
lever l’indétermination.
FI. Il faut
lever l’indétermination.
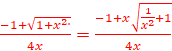 =
=![]()
![]() =
=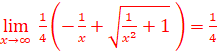
4.![]() =
=![]() FI. Il
faut lever l’indétermination.
FI. Il
faut lever l’indétermination.
![]() =
=![]() =
=![]()
![]() =
=![]() =
=![]()
5.![]() =
=![]() =∞-∞
FI. Il faut lever l’indétermination.
=∞-∞
FI. Il faut lever l’indétermination.
![]() =x(
=x(![]() +3)
+3)
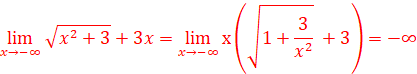
EXERCICE III :
1. Rappeler les limites suivantes :
![]() =1
=1
![]() =1
=1
![]() =1
=1
2. Calculer les limites en 0 de chacune des fonctions
suivantes :
1.![]() =
=![]() .
.![]() =1
=1
2.![]() =
=![]() -
- ![]() =1-1=0
=1-1=0
3.![]() =
=![]() =
=![]()
4.![]() =
=![]()
EXERCICE IV : Peut-on prolonger f par
continuité en 0 ?
1.![]() Df=
Df=![]()
![]() =1 donc on
peut définir une fonction g telle que
=1 donc on
peut définir une fonction g telle que ![]() qui est
le prolongement de f par continuité.
qui est
le prolongement de f par continuité.
2. ![]() Df=
Df=![]()
![]() =1 donc on
peut définir une fonction g telle que
=1 donc on
peut définir une fonction g telle que ![]() qui est
le prolongement de f par continuité.
qui est
le prolongement de f par continuité.
3. ![]() Df=
Df=![]()
![]() =
=![]() =∞
. Donc on ne peut pas prolonger f par continuité.
=∞
. Donc on ne peut pas prolonger f par continuité.
4.
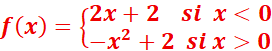
![]()
![]()
On a :
![]()
Merci de votre visite
Laissez un commentaire