NOMBRES PREMIERS

MULTIPLES-DIVISEURS

Effectuons la division de a par b.

On pose :

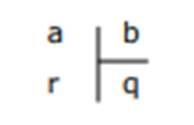
a est la dividende

b est le diviseur

q est le quotient

r est le reste

                                     On écrit : a = bxq +r

Exemple :

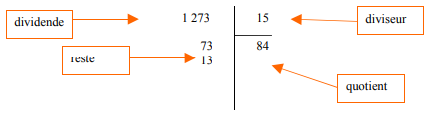
1273=15x84 +13  ici a=1273, b=15, q=84 et r=13

Définition :

Ø On dit qu’un entier a est multiple d’un entier b si le reste de la division de  a par b est zéro.

Ø On dit qu’un entier b est un diviseur d’un entier a si le reste de la division de  a par b est zéro.

Donc si a est un multiple de b alors b est diviseur de a.

Exemples :

4 est un diviseur de 32 car 32 :4=8 et le reste est 0

32 est un multiple 4 pour la même raison.

Critères de divisibilité

NOMBRES PREMIERS

Définition
             Un entier supérieur à 1 est dit premier s’il n’est divisible que par 1 et par lui-même.
Décomposition en facteurs premiers
.             La décomposition d’un entier en produit de facteurs premiers consiste à écrire cet
entier sous la forme d’un produit de ces diviseurs premiers.

dividende	124	62	31	1
diviseur	2	2	31

124 :2=62          //  2 est le plus petit nombre premier différent de 1 qui divise 124.

62 :2=31            // 2 est le plus petit nombre premier différent de 1 qui divise 124.

31 :31=1            //31 est le plus petit nombre premier différent de 1 qui divise 124.

On déduit que 124 =1x 2 x 2 x 31=1x2²x31

NB :2x2=2² on lit « 2 puissance 2 ou 2 exposant 2»

Donc 124=1x2²x31

Méthode :

Pour chercher la décomposition d’un entier en produit de facteurs premiers,
nous pouvons appliquer l’algorithme formel suivant :
• Vérifier si n est divisible par 2, si oui continuer à le diviser par 2 et le remplacer par le quotient de la division de n par 2, jusqu’à ce qu’il ne soit plus multiple de 2
• Refaire l’étape précédente pour les n0mbres premiers qui suivent :  3, 5,7,11,13, ...
• Refaire les deux étapes précédentes jusqu’à avoir n = 1

 Liste des 25 premiers nombres premiers inferieurs à 100 :

2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97

EXERCICES

EXERCICE I :

1.Completer

a-45=2x… + …

b-117=…..x23 +….

c-1223=6x203 + …

d-5040=8x630 +….

2. Enumérer les 5 premiers multiples de : 7,9 et 13

3. Enumérer les diviseurs de : 31,16 et 45

EXERCICE II:

1. Identifier parmi les nombres ci-dessous ceux qui sont premiers : 5 ; 42 ; 41 ; 7 ; 213 ; 81

2. Répondre par VRAI ou FAUX

a-27 est un nombre premier

b-13 est un nombre premier

EXERCICE III:

1) Décomposez 124 en produits de facteurs premiers. Refaites le même calcul pour les entiers 348 et 432.
2) Comment faire pour décomposer un entier donné en produit de facteur premiers ?

EXERCICE IV :

Le service des espaces verts veut border un espace rectangulaire de 924 m de long sur 728 m de large `à l’aide d’arbustes régulièrement espaces : la distance entre deux arbustes consécutifs doit être constante, égale a un nombre entier de mètres. Un arbuste sera place à chaque angle du terrain.

1) Déterminer toutes les valeurs possibles de la distance entre deux arbustes.

2) Déterminer, dans chaque cas, le nombre d’arbustes nécessaires `a la plantation.

CORRIGES:

Exercice I :

1.Completons :

a-45=2x22 + 1

b-117=5.x23 +2

c-1223=6x203 + 5

d-5040=8x630 +0.

2-Multiples de 7 :7, 14, 21,28…

Multiples de 9 :9, 18, 27, 36,45…

Multiples de 13 :13, 26, 39,42…

3-Diviseurs de 31 :1

Diviseurs de 16 :1, 2, 4, 8,16

Diviseurs de 45 :1, 3, 5, 9,15

Exercice II:

1. Nombres premiers : 5 ; 41 ; 7 

2. Répondre par VRAI ou FAUX

a-27 est un nombre premier : Faux

b-13 est un nombre premier : vrai

Exercice III:

Pour écrire l’entier 124 en produit de facteurs premiers, nous pouvons dresser
puis remplir le tableau suivant :

dividende	124	62	31	1
diviseur	2	2	31

dividende	348	174	87	29	1
diviseur	2	2	3	29

En déduire que 124 = 2 x 2 x 31
Nous ferons de même pour les entiers 348 et 432. En effet :
En déduire que 348 = 2 x 2 x 3 x 29

dividende	432	216	108	54	27	9	3	1
diviseur	2	2	2	2	3	3	3

En déduire que 432 = 2 x 2 x 2 x 2 x 3 x 3 x 3

Ou verticalement :

124 62 31 1

2 2 31

//2 est le plus petit nombre premier différent de 1 qui divise 12

 //2 est le plus petit nombre premier différent de 1 qui divise 62

//31 est un nombre premier, ses seuls diviseurs sont 1 et lui-même

         124=2x2x31x1=1x2²x31

348 174 87 29 1

2 2 3 29

//2 est le plus petit nombre premier différent de 1 qui divise 348

//2 est le plus petit nombre premier différent de 1 qui divise 174

//3 est le plus petit nombre premier différent de 1 qui divise 87

//29 est un nombre premier, ses seuls diviseurs sont 1 et lui-même

348=2x2x3x29x1=2²x3x29x1

Merci de votre visite
Laissez un commentaire