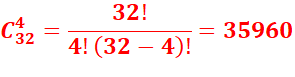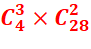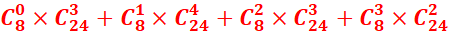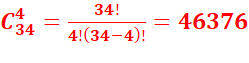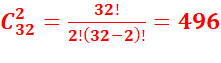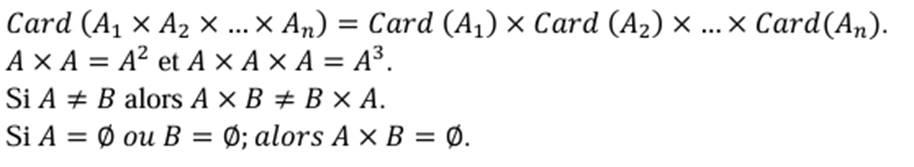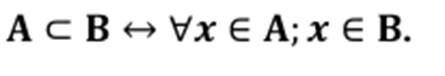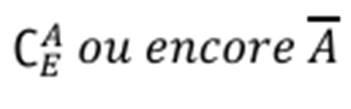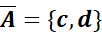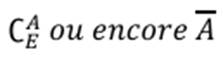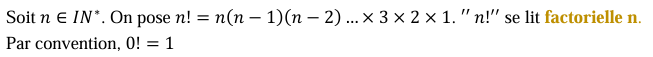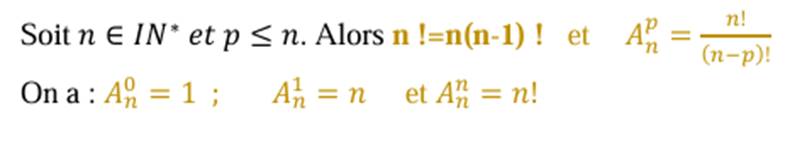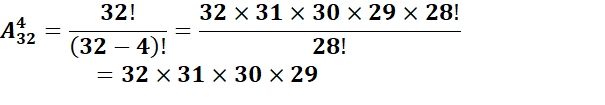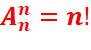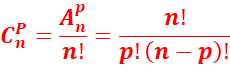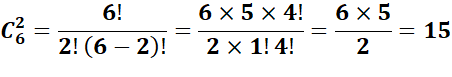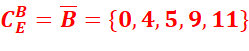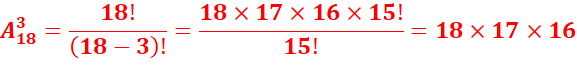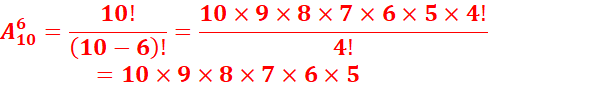DENOMBREMENT
GENERALITES
Cardinal d’un ensemble
fini
Ø Un ensemble qui
n’a aucun élément ou qui possède un nombre fini d’éléments
est ensemble
fini.
Soit n un entier naturel et A un ensemble.
A= {1,2,3,4…n} est un ensemble fini si on peut compter tous ses
éléments.
Ø Le nombre
d’éléments d’un ensemble fini A est le cardinal de A. On le note card (A).
Exemple : card (A)=n
Propriétés
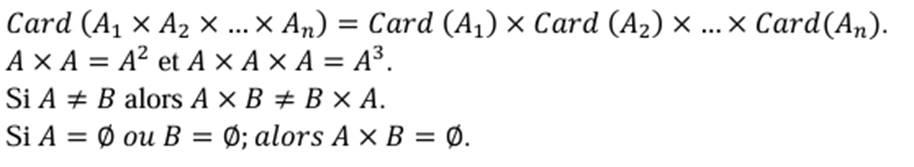
Inclusion
Soient A, B et E trois ensembles finis.
On dit que A est une partie
de B si et seulement si tous les éléments de A sont aussi éléments de B.
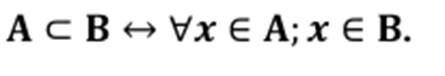
On dit que A est
inclus dans B et on
note A 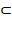 B
B
Exemple :
B= (1,2,3,4,5,6.7,8,9,0}
A= (1,2,3,4}
A 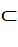 B
B
Complémentaire
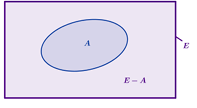
Ø Le complémentaire de A dans E est
l’ensemble des éléments de E qui ne sont pas dans A. On note :
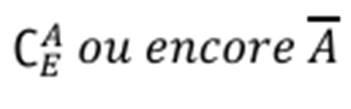
Exemple :
E= { a, b, c, d}
A= { a, b }
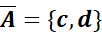
Réunion et Intersection
des parties d’un ensemble
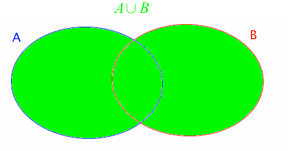
La réunion de A et B est l’ensemble des éléments de E qui sont dans A
ou dans B. On note : AUB
Exemple :
A={ a, b, c, d}
B={ a, b ,4.5}
AUB ={a,b,c,d,4,5}
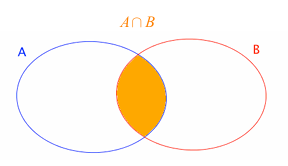
L’intersection
de A et B est l’ensemble des éléments de E qui sont à la fois dans A et dans B.
On note : A⋂B
Exemple :
A={ a, b, c, d}
B={ a, b ,4.5}
A⋂B= {a, b}
Remarque :
Deux ensembles A
et B sont disjoints si A⋂B= ∅. (∅ désigne l’ensemble vide)
(∅ désigne l’ensemble vide)
Propriétés :

Ø Soit E un
ensemble non vide.
Un ensemble de parties de E forme une partition de E si :
-Elles sont non vides.
-Elles sont deux
à deux disjointes.
-Leur réunion est égale à E.
Exemple :
E : ensemble des
lettres de l’alphabet français
A :
ensemble des consonnes
B :
ensemble des voyelles
A et B forment
une partition de E
Ø Soient A et B
deux ensembles non vides. On appelle produit cartésien de A par B l’ensemble noté A x B et défini par :
AxB= {(a,b) ;
a ϵ A ;b ϵ B }.
Exemple :
A={a,b}
B=(1,2)
AxB={(a,1) ; (a,2) ;
(b,1) ; (b,2) }
Remarque :
Card (AxB)=Card A x Card B
OUTILS GRAPHIQUES DE
DENOMBREMENT
Utilisation d’un Diagramme
de VEEN
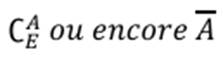
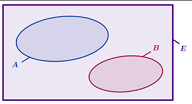 A⋂B= ∅.
A⋂B= ∅.
Utilisation d’un Tableau
a double entrée

Utilisation d’un Arbre a
choix
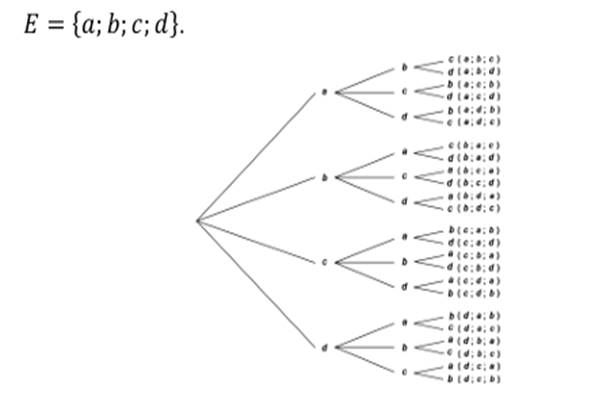
ANALYSE COMBINATOIRE
p-uplets
Définition : Soit E un ensemble fini
à n éléments, p un entier naturel non nul.
On appelle p-uplet ou p-liste d’élément de E
une suite
ordonnée de p éléments de E non nécessairement tous distincts.
C’est un élément
de l’ensemble :
Ep =E x E x…x E
Propriété :
. Le nombre de
p-uplet de E est np
Remarque :
·
Un p-uplet est une disposition ordonnée dans laquelle
un même élément
peut être répété jusqu’à p fois.
·
On utilise les p-uplets dans une épreuve à
tirages successifs avec remise.
·
Deux p-uplets diffèrent soit par la nature
des éléments de E qui le constituent, soit par l’ordre des éléments.
Exemple :
L’épreuve du
lancer de dé comporte 6 résultats possibles. On lance le dé 4 fois et on note
les résultats obtenus. Il y a 64=64
résultats possibles. Le résultat d’un tel évènement est ce qu’on appelle une
4-liste dans un ensemble a 6 éléments.
Arrangements
Définition :
Soit E un ensemble
fini à n éléments, p un entier naturel non nul plus petit que n. On appelle
arrangement de p élément de E, tout p-uplet formés
d’éléments 2 à 2 distincts.
Propriété
: Soit E un ensemble à n éléments, p un entier
naturel non nul plus petit que n. le nombre d’arrangements de p éléments de E
est :
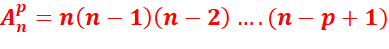
Remarques :
·
Un arrangement est une disposition ordonnée sans répétition.
·
On utilise les arrangements dans une épreuve à tirage successifs
sans remise.
Notion de factoriel :
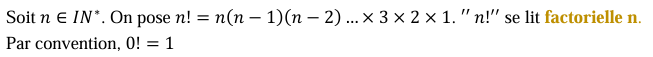
Propriété :
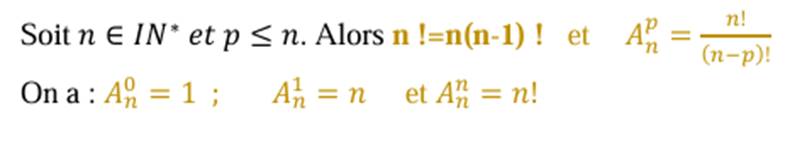
Exemple : On tire 4 cartes successivement sans remise
dans un jeu de 32 cartes. Il s’agit du nombre d’arrangements de 4 éléments pris
dans un ensemble a 32 éléments.
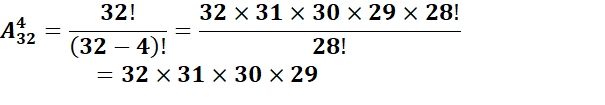
Permutations
Définition :
Soit E un ensemble fini non vide à n éléments.
On appelle permutation
de E tout
arrangement ou p-uplet sans répétition des n
éléments de E.
Remarques.
·
Le nombre de permutations d’un ensemble fini E à n élément est :
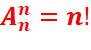
·
Le tirage successif sans remise
de n objets parmi n est assimilable à une permutation des n éléments d’un
ensemble.
·
Une anagramme d’un mot dont les
lettres sont toutes distinctes est une permutation des lettres de ce mot.
Exemple : on donne
l’ensemble E={1,2,3} 8n peut former 3 ! =6
nombres de 3 chiffres.
Combinaisons
Définition
:
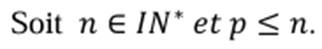
On appelle
combinaison de p éléments de E toute partie (sous ensemble) de E ayant p
élément.
Propriété
:
Le nombre de combinaison de p éléments d’un
ensemble à n éléments est :
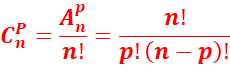
Remarques :
·
Une combinaison est une disposition non ordonnée et sans répétition.
·
On utilise les combinaisons dans une épreuve à tirages simultanés.
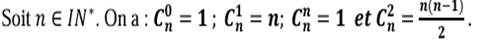
Exemple : Une urne
contient 6 boules numérotés de 1 à 6. On tire simultanément 2 boules. Il y a 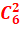 de tirages
possibles
de tirages
possibles
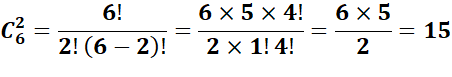
Propriétés :
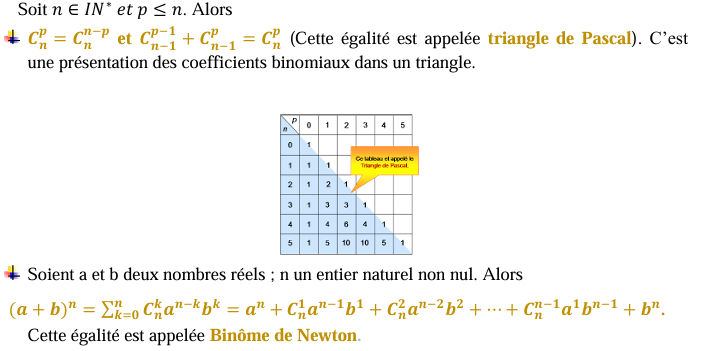
Recapitulons
Pour déterminer
le nombre de tirages de p éléments d’un ensemble E a n éléments (p≤n), on peut utiliser le tableau suivant :
Modélisation
|
Les p éléments sont ordonnes
|
Les p éléments sont distincts
|
outil
|
Nombre de tirages
|
Tirages successifs avec remise
|
oui
|
non
|
p-uplet
|
np
|
Tirages successifs sans remise
|
oui
|
oui
|
Arrangement de p éléments de E
|
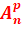
|
Tirages simultanées
|
non
|
oui
|
Combinaison de p éléments de E
|
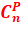
|
EXERCICES
EXERCICE I:
soient 3
ensembles E, A et B
1. Ecrire en
extension : A, B, E, AUB, A⋂B, 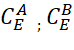
2.A et B
forment-ils une partition E ? pourquoi ?
3.Donner card(AUB)
et card(A⋂B).
Vérifier que card(AUB)= card(A)+ card(B) - card(A⋂B)
EXERCICE II:
Un restaurant propose sur sa carte 3 entrées, 4 plats de résistance et
2 desserts.
a) Combien de
menus différents composés d’une entrée, d’un plat et d’un dessert peut-on
constituer ?
b) Même question
si le dessert de banane est imposé.
EXERCICE III :
Dans une classe de première littéraire de 50 élèves, 24 élèves ont 16
ans,14 élèves ont 17 ans et les autres ont plus de 17 ans. 23 élèves ont opté
pour l’espagnol comme langue vivante II, l’espagnol et les autres ont opté pour
l’allemand comme langue vivante II,13 élèves ont16 ans et font
l’espagnol ;10% des élèves ont plus de 17 ans et font l’allemand.
1.Completer le
tableau a double entrée suivant :
|
16 ans
|
17 ans
|
>17 ans
|
Total
|
ESP
|
|
|
|
|
All
|
|
|
|
|
Total
|
|
|
|
50
|
2.Quelle est la
répartition en âge des élèves qui ne font pas d’espagnol ?
3.Combien
d’élèves n’ont pas 16 ans et ne font pas espagnol ?
EXERCICE IV :
Un magasin souhaite faire une promotion sur des lampes de bureau et de
lampes de salon. Ces lampes sont couleur blanche, noire et rouge. Sur ces 200
lampes,25% sont des lampes de salon. On sait que 30% des lampes sont blanches.
Il y a 60 lampes rouges et parmi elles, 20% sont des lampes de salon. Le quart
des lampes noires est constitué de lampes de salon.
Compléter le
tableau a double entrée suivant :
|
Blanche
|
Noire
|
Rouge
|
Total
|
Lampes de
bureau
|
|
|
|
|
Lampes de
salon
|
|
|
|
|
Total
|
|
|
|
|
EXERCICE V:
1.Determiner le
nombre de façons distinctes de ranger 3 livres dans 4 tiroirs sachant que plus
d’un livre peuvent être rangés dans un même tiroir.
2.Pour une course
impliquant 18 chevaux, déterminer le nombre des 3 premiers chevaux dans l’ordre
et sans ex-aequo.
3.Determiner le
nombre de façons de ranger 6 voitures en disposant de 10 parkings.
4.Combien de
mots deux a deux distincts peut-on former avec les lettres REGAIN ?
TABLEAU ?
EXERCICE VI :
On dispose d’un jeu de carte de
32 cartes. Un jeu de 32 cartes est composé de 4 couleurs (Trèfle, Carreau, Cœur
et Pique). Dans chaque couleur il y a 8 cartes.
a) Calculer le
nombre de façons de tirer simultanément 4 cartes parmi 32.
b) Déterminer le
nombre de combinaisons de 5 cartes ayant exactement 3 As
c) Déterminer le
nombre de combinaisons de 5 cartes contenant au plus 3 trèfles.
d) Calculer le
nombre de façons de tirer au moins un As.
EXERCICE
VII :
Une classe composée de 18 filles et 16 garçons va élire les 4 délégués.
Dans cet exercice, on ne distingue pas les délégués et les délégués-adjoints.
a) Combien
existe-t-il de possibilités pour cette élection ?
b) Emma dit
qu’elle ne souhaite pas être élue si Bastien est élu. Dans ces conditions,
combien existe-t-il de possibilités ?
CORRIGES
EXERCICE I :
1. A={0,1,4,5,7}
B={1,3,7,17}
A⋂B={1,7}
AUB={0,1,4,5,7,3,17)
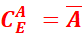 ={3,17,9,11}
={3,17,9,11}
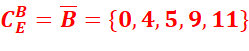
2.non car A et B ne sont pas disjoints.
3. card(AUB)=7 card(A⋂B)=2 card(A)=5 card(B)=4
=>7=5+4-2
EXERCICE II:
a)
Soit 𝐸
l’ensemble des entrées, 𝑃 celui
des plats et 𝐷 celui
des desserts. On considère alors les triplets de la forme (entrée, plat,
dessert) éléments de 𝐸 × 𝑃 × 𝐷. D’après le principe multiplicatif,
on a : c𝑎𝑟𝑑(𝐸 ×𝑃×𝐷) =𝐶𝑎𝑟𝑑(𝐸)×𝐶𝑎𝑟𝑑(𝑃)×𝐶𝑎𝑟𝑑(𝐷) = 3×4×2 = 24. Il existe 24 menus
différents.
b) 𝐶𝑎𝑟𝑑 (𝐸 × 𝑃) = 𝐶𝑎𝑟𝑑(𝐸)×𝐶𝑎𝑟𝑑(𝑃) = 3×4 = 12 Il existe 12 menus
différents dont le dessert est de la banane.
EXERCICE III :
1.
|
16
ans
|
17
ans
|
>17ans
|
Total
|
Espagnol
|
13
|
3
|
7
|
23
|
Allemand
|
11
|
11
|
5
|
27
|
Total
|
24
|
14
|
12
|
50
|
2.
La répartition en âge des élèves qui ne font pas d’espagnol est :
11
élèves de 16 ans
11
élèves de 17 ans
5 élèves de plus de 17 ans
3.16
n’ont pas 16 ans et ne font pas espagnol ?
EXERCICE IV :
|
Blanche
|
Noire
|
Rouge
|
Total
|
Lampes
de bureau
|
42
|
60
|
48
|
150
|
Lampes
de salon
|
18
|
20
|
12
|
50
|
Total
|
60
|
80
|
60
|
200
|
EXERCICE V :
1.
C’est une p-liste : 43 façons distinctes.
2.
C’est un arrangement :
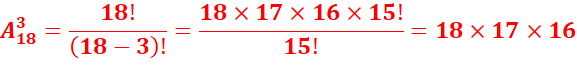
3.
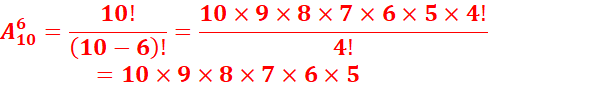
4. On peut former 6! = 6x5x4x3x2x1=720
anagrammes du mot REGAIN
En ce qui concerne TABLEAU, le A se répète.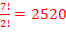 anagrammes.
anagrammes.
EXERCICE
VI :
a)
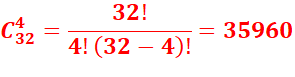
b)
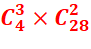
c)
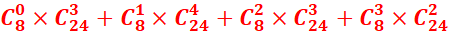
d)

EXERCICE
VII :
a)
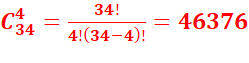
b)
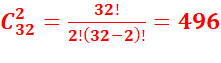
Le
nombre de possibilités est égal a 46376-496=45880
Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire
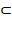 B
B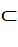 B
B (∅ désigne l’ensemble vide)
(∅ désigne l’ensemble vide) A⋂B= ∅.
A⋂B= ∅.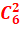 de tirages
possibles
de tirages
possibles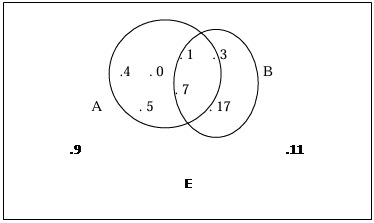
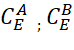
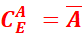 ={3,17,9,11}
={3,17,9,11}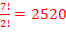 anagrammes.
anagrammes.