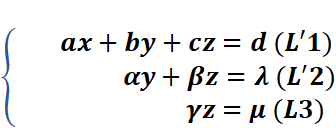SYSTEMES LINEAIRES
Système
linéaire de trois équations à 3 inconnues
Méthode du pivot
de GAUSS.
Soit un système linéaire (S) défini comme suit :
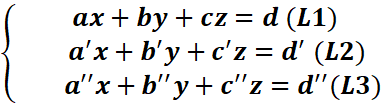
La méthode du pivot de GAUSS consiste à transformer un système linéaire en un
système triangulaire équivalent en exécutant des opérations
élémentaires sur les lignes :
-échange de
deux lignes Li et Lj (Li↔Lj).
-remplacement
de la ligne Li par la combinaison λLi
obtenu en multipliant chaque coefficient de Li par le nombre réel
λ suppose non nul (Li←λLj).
-remplacement
de la ligne Li par la combinaison αLi+βLj obtenu en additionnant membre a membre les
lignes αLi et βLj,
α étant un nombre réel non nul et β un nombre quelconque (Li←
αLi+βLj).
On doit obtenir un système équivalent au
système (S’) ci-après :
Remarque :
-Deux systèmes sont dits équivalents lorsqu’ils ont le même ensemble solution.
-Lorsqu’on remplace une équation d’un système par la combinaison linéaire des
équations du système, On obtient un système équivalent au système initial.
La méthode du pivot de GAUSS se déroule
comme suit :
I- Fixer une des trois équations qu’on appelle pivot (supposons que notre pivot
ici est (L1))
II- Utiliser le pivot pour éliminer l’inconnue x dans les équations (L2)
et (L3); on obtient ainsi les équations (L’2) et
(L’3) respectivement qui ne dépendent que des inconnues y et z.
III- On
fixe une des équations (L’2) et (L’3) (supposons qu’on a
fixé (L’2) puis on l’utilise pour éliminer l’inconnue y dans
l’équation (L’3)); ce nous conduit à l’équation (L’’3)
qui ne dépend que de z.
IV- Le système triangulaire ( S’) est
donc le système formé par (L1),(L’2) et (L’’3)dans
cet ordre pour ce cas de figure.
Exemple :
Soit le système (S) suivant :
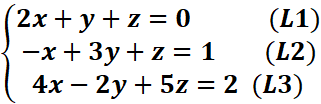
Fixons la première équation L1 comme pivot de Gauss et
transformons le système (S’) en un système triangulaire équivalent.
Pour éliminer x dans L1 et dans L3
On remplace : L2 par L1+2L2
L3 par -2L1 +L3
On obtient le système suivant :
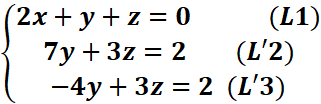
Pour éliminer y dans L’3
On remplace L’3 par 4L’2+7L’3
On obtient le système triangulaire suivant :
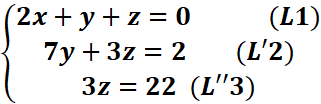
S= {(-1/3 ;0 ;2/3)}
Système
linéaire de deux équations à 3 inconnues

Exemple :
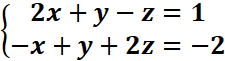
Choisissons l’une des trois inconnues, par exemple z comme paramètre. On
ramène le système (S) a un système (S’) de deux équations a
deux inconnues :
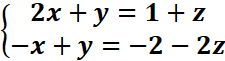
Posons z= λ ϵ IR
On a :
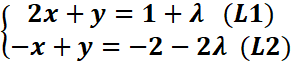
Trouvons les valeurs de x et y en fonction de λ
L1+2L2 =>3y=1+λ-4-4λ =-3-3λ
=>y=-1-λ
x=y+2+2λ=-1-λ+2+2λ=1+λ
La résolution de (S’) conduit à la solution définie par :
x=1+λ ; y=-1-λ ;z=λ (λ ϵ
IR)
Le système (S) a donc une inimité de solutions
constituées des triplets (1+λ ; -1-λ ; λ)
EXERCICES
EXERCICE I:
1. Résoudre par substitution, puis par la
méthode du pivot de Gauss le système :
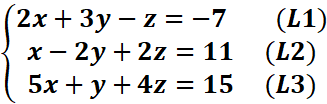
2. Résoudre par substitution, puis par la
méthode du pivot de Gauss le système :
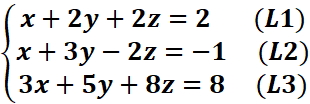
3.
Résoudre par substitution, puis par la méthode du pivot de Gauss le système :
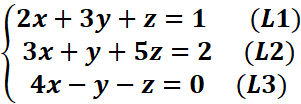
4. Résoudre
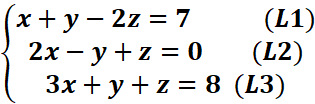
5.
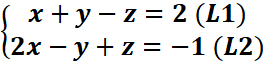
EXERCICE II:
Anna se rend à la banque et retire au guichet
une somme de 725€.La banquière lui remet 45 billets dont :
- des billets de 5€
-des billets de 10€
-des billets de 20€
A la sortie de la banque, elle se rend dans un supermarché.
Après son passage la caisse, il lui reste la moitié des billets de 10€, la
moitié des billets de 20€, et toujours le même nombre de billets de 5€ et une
somme totale de 375€.
Combien Anna avait-elle des billets de 5€,10€ et 20€ à la
sortie de la banque ?
EXERCICE III:
Un potier fabrique trois types différents A,B,C et D de canaris.
Pour fabriquer un canari de type A, le potier a besoin
de : 40kg d’argile.60litres d’eau et 15 kg de bois de chauffage.
Pour fabriquer un canari de type B, le potier a besoin de : 18kg d’argile.20litres
d’eau et 7 kg de bois de chauffage.
Pour fabriquer un canari de type C, le potier a besoin
de : 70kg d’argile.110litres d’eau et 35 kg de bois de chauffage
En une semaine, le potier utilise pour la fabrication
de ses canaris :3656kg d’argile,5040litres d’eau et 1494 kg de bois de chauffage
Déterminer le nombre de canaris de chaque type que ce
potier fabrique ainsi en une semaine..
CORRIGES :
EXERCICE
I :
1.
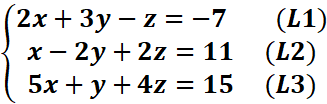
Par substitution :
De la deuxième équation
(L2), on tire x en fonction de y et z
![]()
On remplace x dans les deux
autres
![]() =>
=>![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
x=11+2y-2z < = > x=11+2(-2)-2(3)=1 =>. S=![]()
Par le pivot de Gauss
Choisissons L1
comme pivot
Faisons L1-2L2
=>![]()
0x + 7y - 5z= -29 =>7y – 5z= -29
Faisons 5L1-2L3=>![]()
0x + 13y - 13z= -65 =>13y – 13z= -65
Le système devient :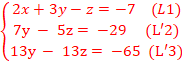
Faisons 13L’2-7L’3=>![]()
. –26z=-78
Le système
devient :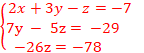
De –26z=-78 => z=3
De 7x-5z=-29 =>7y-5(3)=-29 => 7y=-14 =>y=-2
De 2x +3y-z=-7 => 2x + 3(-2)-3=-7=>2x=2=>x=1
4.
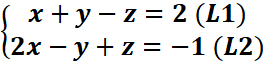


5.

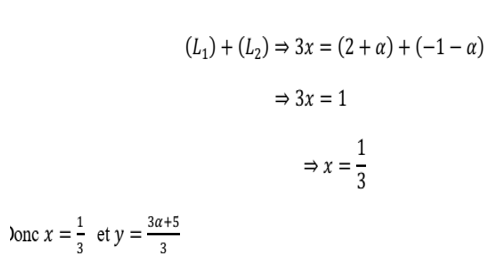
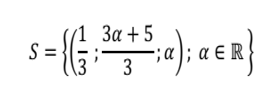
EXERCICE
II :
Soient :
x : le nombre de billets de 5€
y : le nombre de billets de 10€
z : le nombre de billets de 20€
Valeur totale des billets sortis de la banque :
5x + 10y +20z=725
Nombre total des billets :
x+y+z=45
Valeur totale des billets sortis de du supermarché : 5x + (10)(y/2)
+(20)(z/2) =375
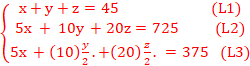 =>
=>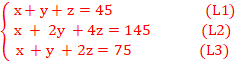
Choisissons L1 comme pivot
L1-L2 donne(x+y+z=45)-(x+2y+4z=145)
=> -y-3z=-100
L1-L3 donne (x+y+z=45) - (x+y+2z=75)
=>-z=-30
Le système devient 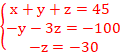
De -y-3z=-100 <=>-y-3(30) =-100=> y=10
De x+y+z=45<=>x +10
+30=45=>x=5
EXERCICE III:
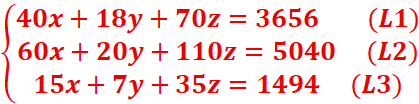
S={(38 ;72 ;12)}
En une semaine, le potier fabrique 38 canaris, de type A,72
canaris de type B et 12 canaris de type C.
Avez-vous un exercice à proposer ?
Cliquez-ici
Merci de votre visite
Laissez un commentaire