STATISTIQUES

SERIE STATISTIQUE DOUBLE

Tableaux linaires.

On considère les notes obtenues en Maths et Compta par 10 élèves Tle CG représenté dans le tableau suivant :

Elève	A	B	C	D	E	F	G	H	I	J
Note Compta	6	9	13	9	10	11	9	11	12	14	X
Note Maths	11	13	12	13	9	10	13	10	9	7	Y

Tableau 1

Ø On désigne par P la population étudiée, ici il y a deux caractères :

X : le caractère ‘’ Note de Compta’’.

Y : le caractère ‘’ Note Maths ‘’

Ø On désigne par M_i les modalités, ici il y a deux modalités :

M_X={6, 9, 13,10, 11, 12, 14}

M_X={11, 13,12, 9, 10, 7}

L’effectif de la modalité 13 du caractère Y est 3.

Tableau à double entrée

Partant du tableau 1, on peut utiliser un tableau à double entrée.

	6	9	10	11	12	13	14	←Compta
7	0	0	0	0	0	0	1
9	0	0	1	0	1	0	0
10	0	0	0	2	0	0	0
11	1	0	0	0	0	0	0
12	0	0	0	0	0	1	0
13	0	3	0	0	0	0	0
↑Maths

Tableau 2

// il y a 3 personnes qui ont 13 en Maths et 9 en Compta.

// il y a 2 personnes qui ont 10 en Maths et 11 en Compta.

Séries statistiques marginales

On complète le tableau a double entrée en mettant en évidence d’une part les effectifs des modalités du caractère X, d’autres parts les modalités du caractère Y. On obtient un autre tableau permettant la distribution statistique associée à X et celle associée à Y. Ces séries sont respectivement appelée série marginale associée à X ou de caractère X et série marginale associée à Y ou de caractère Y.

	6	9	10	11	12	13	14	ni
7	0	0	0	0	0	0	1	1
9	0	0	1	0	1	0	0	2
10	0	0	0	2	0	0	0	2
11	1	0	0	0	0	0	0	1
12	0	0	0	0	0	1	0	1
13	0	3	0	0	0	0	0	3
ni	1	3	1	2	1	1	1	10

Tableau 3
on déduit les tableaux linéaires suivants :

Tableau linéaire associe à X

xi	6	9	10	11	12	13	14	Total
ni	1	3	1	2	1	1	1	10

Tableau linéaire associe à Y

yi	7	9	10	11	12	13	Total
ni	1	2	2	1	1	3	10

Nuage de points associe à une série double

X et Y sont deux caractères définis sur une population P

{x₁, x₂,…,x_p} .l’ensemble M_X des modalités du caractère X

{y₁, y₂,…,y_p} .l’ensemble M_Y des modalités du caractère Y

Définition : Dans un repère orthogonal, l’ensemble des points 𝑀𝑖 de coordonnées (𝑥𝑖, 𝑦𝑖) constitue le nuage de points associé à la série statistique à deux variables.

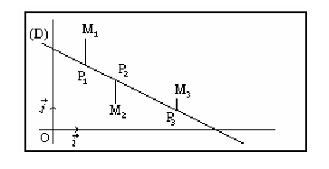
On peut utiliser la représentation du nuage par un ensemble de points pondérés c.-à-d. on indique à coté de chaque point 𝑀𝑖 de coordonnées (𝑥𝑖, 𝑦𝑖) l’effectif. Une autre variante de ce type de représentation est la représentation par tâche c.-à-d. chaque point 𝑀𝑖 de coordonnées (𝑥𝑖, 𝑦𝑖) est représenté par un disque dont l’aire est proportionnelle à l’effectif.

Point moyen d’un nuage représentant une série double

Le point moyen du nuage de la série statistique à deux variables est le point M dont les coordonnées sont les moyennes ( ) des X et Y respectivement.

AJUSTEMENT LINÉAIRE :

Soit (xi, yi) une série statistique double, avec un nuage de points Mi (xi, yi) associé. Lorsque les points du nuage paraissent presque alignés, on peut chercher une relation de la forme y = ax + b qui exprime de façon approchée les valeurs de la série (y i) en fonction des valeurs de la série (xi) , autrement dit, une fonction affine f telle que l’égalité y = f(x) s’ajuste au mieux avec les données. Graphiquement, cela signifie qu’on cherche une droite qui passe au plus près de tous les points du nuage. Une telle relation permettrait notamment de faire des prévisions. Il existe de nombreuses manières d’obtenir un ajustement affine satisfaisant.

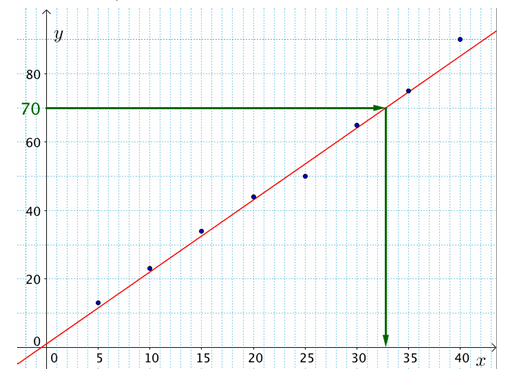
Ajustement graphique linéaire par la méthode de MAYER

Etape 1 : On commence par « découper » la série statistique double en deux sous-séries bien distinctes, c’est-à-dire que l’on découpe le nuage de points Mi (xi, yi) en deux sous-nuages distincts et de même effectif (ou presque : si le nombre de points est pair, pas de souci. S’il est impair, on peut mettre le point surnuméraire dans n’importe lequel des deux sous-nuages)

Etape 2 : On calcule les coordonnées des deux points moyens G₁ et G₂ associés à ces deux sous nuages, et on place ces deux points sur le graphique.

Etape 3 : On trace la droite (G₁ G₂), appelée droite de Mayer du nuage de points Mi (xi, yi), qui doit passer par le point moyen G du nuage de points Mi (xi, yi). C’est cette droite qui constitue un ajustement affin tout à fait acceptable pour la série double (xi, yi).

Exemple :

xi	60	70	90	110	130	150
yi	3	3.1	3.7	4.7	6	9

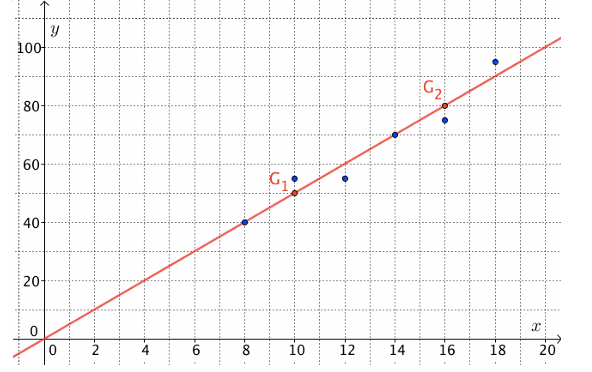
= (8 + 10 + 12) : 3 = 10

= (40 + 55 + 55) : 3 = 50.

Le point moyen G₁ a pour coordonnées (10 ; 50).

= (14 + 16 + 18) : 3 = 16

= (70 + 75 + 95) : 3 = 80

Le point moyen G₂ a pour coordonnées (16 ; 80).

Ajustement affine par la méthode des moindres carres

Covariance d’une série statistique double

On appelle covariance de la série double (xi, yi) le nombre note Cov(X,Y) tel que :

.

Coefficient de corrélation

On appelle coefficient de corrélation linéaire du couple (X, Y), le nombre réel, noté r tel que :

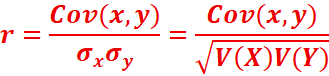
Droites de régression

· On considère un nuage de points Mi (xi, yi) et soit (D) une droite d’équation y = ax + b que l’on cherche à déterminer.

La droite (D) d’équation y = ax+b où a et b sont déterminés d’après les relations ci-dessus, est appelé droite de régression de Y en X .

· La droite (D’) d’équation : x=a’y+b’ avec :

est appelée droite de régression de X en Y

Remarque 1 :

Les deux droites de régression de Y en X et de X en Y passent toutes deux par le point moyen de coordonnées ( )

Remarque 2 :

· -1 ≤ r ≤ 1

· aa’ = r²

· Lorsque la corrélation est forte (r² ≥ ¾) les droites de régression sont très proches et le nuage peut être approximé par une droite.

· Lorsque la corrélation est faible, le nuage de points ne peut pas être ajusté par une droite, mais il se peut qu’une autre courbe permette un bon ajustement.

EXERCICES

EXERCICE I :

Un responsable de vente des produits laitiers analyse l’évolution de son chiffre d’affaires sur les 10 dernières années. Il relève pour cela le montant des frais de publicité engages sur la même période. Il dresse le tableau suivant (les montants sont exprimés en dizaines de millions).

Frais de publicite (xi)	6	6,5	6,8	7	7,8	9	10,5	11	11,3	11,5
Chiffre d’affaire(yi)	220	229	225	237	235	247	250	268	258	264

1. Déterminer les coordonnées du point moyen G de cette série.

2. Déterminer les coordonnées de G₁, point moyen du 1^er groupe.

3. Déterminer les coordonnées de G₂, point moyen du 2eme groupe.

4. Déterminer l’équation cartésienne de la droite passant par G₁ et G₂.

EXERCICE II :

C,

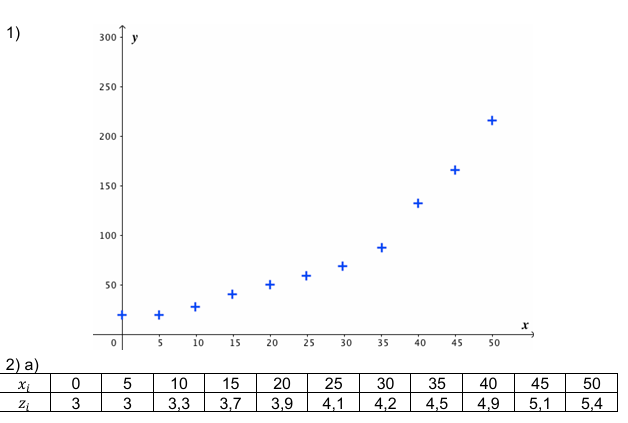
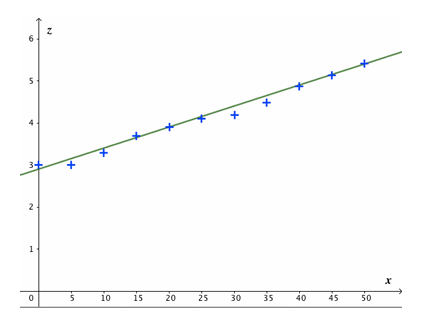
1. Tracer le nuage des points.

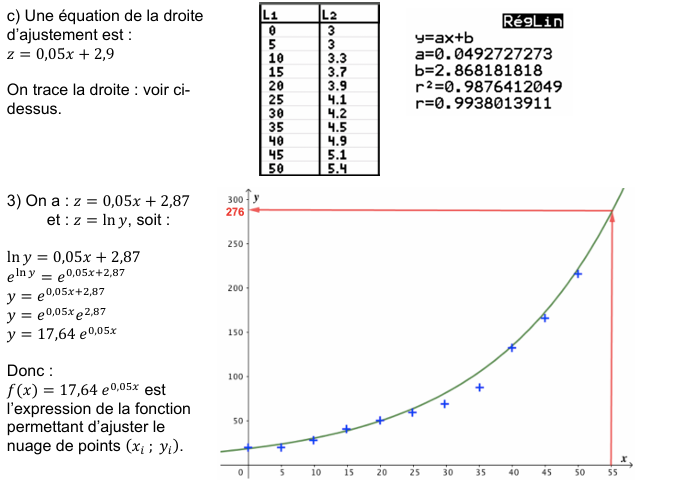
2.Determiner la droite d’justement parla methode des moindres carres.

EXERCICE III :

Dans la série statistique suivante, X représente le nombre de jours d’exposition au soleil d’une feuille et Y le nombre de stomates aérifères au millimètre carré :

1. Tracer le nuage des points.

2. Calculer le coefficient de corrélation linéaire entre X et Y. Conclusion ?

3. Déterminer l’équation de la droite de régression de Y en fonction de X.

4. Si on expose au soleil une feuille 15 jours; quel est le nombre de stomates aérifères peut-on prévoir ?

EXERCICE IV:

Afin d’orienter ses investissements, une chaine d’hôtel réalise des analyses sur le taux d’occupation des chambres. Une analyse établit un lien entre le taux d’occupation exprimé en % et les années de fonctionnement.

Frais de publicité (xi)	30	27	32	25	35	22	24	35
Taux d’occupation(yi)	52	45	67	55	76	48	32	72

1.Determiner les coordonnées du point moyen

2.Determiner la variance de x, celle de y, la covariance du couple (x,y) ainsi que le coefficient de corrélation.

3. Déterminer par la méthode des moindres carres une équation cartésienne de la droite de régression de y en x

4.Quelle estimation peut-on faire du taux d’occupation des chambres de cet hôtel si les frais de publicité étaient de 4 000 0000frs

EXERCICE V:

EXERCICE VI:

CORRIGES :

EXERCICE I :

1. Déterminons G.

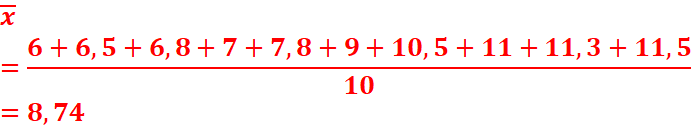
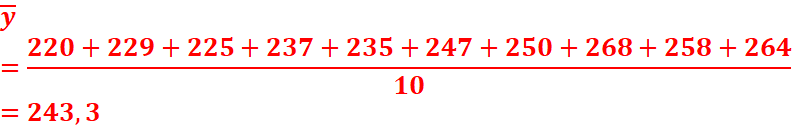
2. Déterminons G1.

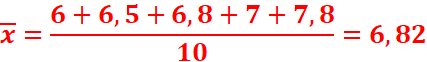
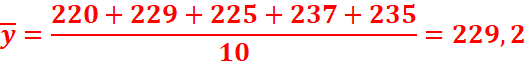
3. Déterminons G2.

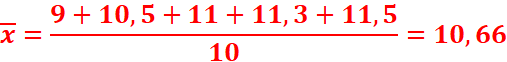
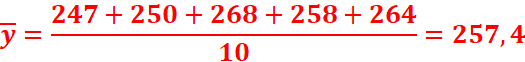
4. Déterminons l’équation cartésienne de la droite passant par G₁ et G₂.

y=ax +b avec

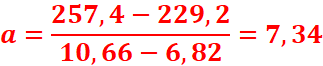
b=229,2-7,34x6,82=179,14

L’équation de (G1, G2) est y=7,34x +179,4

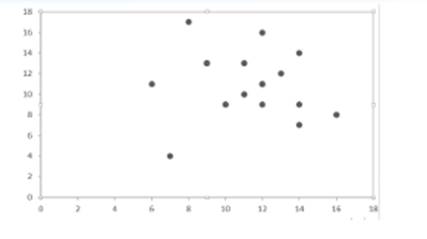
EXERCICE II :

1.

EXERCICE III:

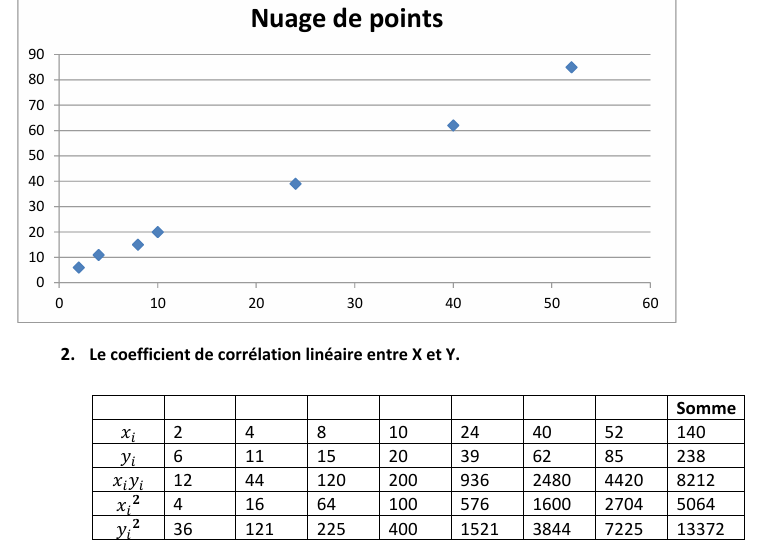
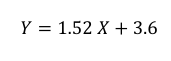
EXERCICE IV:

xi	30	27	32	25	35	22	24	35	230
yi	52	45	67	55	76	48	32	72	447
(xi)^2	900	729	1024	625	1225	484	576	1225	6788
(yi)^2	2704	2025	4489	3025	5776	2304	1024	5184	26531
xiyi	1560	1215	2144	1375	2660	1056	768	2520	13298

1.

2.

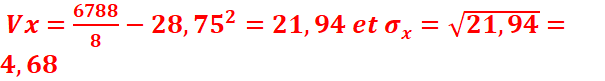
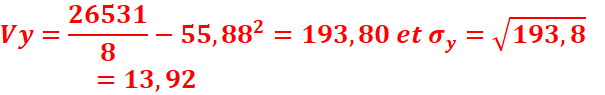
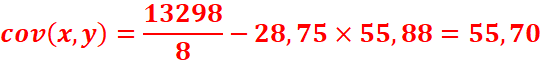
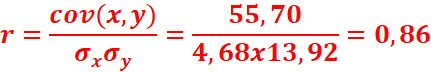
4. y=ax +b avec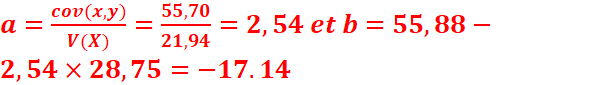

Donc y=2,54x – 17,14

5. x=40 (centaines de millions)

y=2,54x40-17,14=84,46%

EXERCICE V:

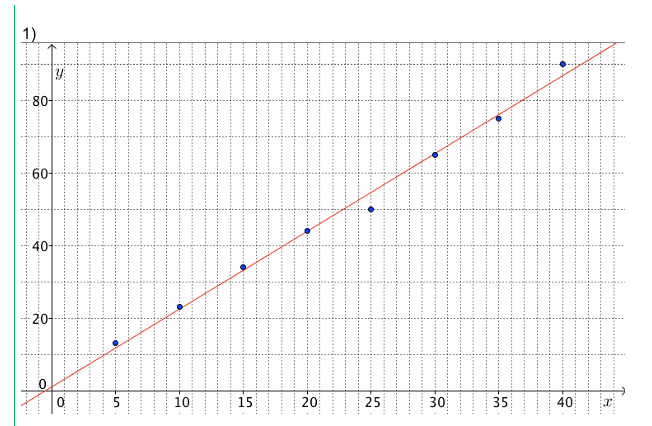
EXERCICE VI :

//On appelle somme des résidus associée à la droite (D), le nombre réel S défini par :

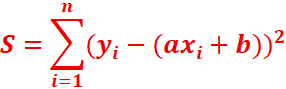
Si Pi désigne le point d’abscisses x_i sur la droite (D), on a :

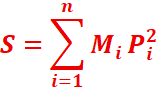
On appelle méthode des moindres carrés la méthode qui consiste à rechercher les coefficients a et b tels que la somme S soit minimale. Remarquons que S est une fonction des deux variables a et b.

Avez-vous un exercice à proposer ? Cliquez-ici

Merci de votre visite
Laissez un commentaire