SYSTEMES D'EQUATIONS ET D'INEQUATIONS
SYSTEMES D'EQUATIONS
Définition :
On appelle système linéaire de deux
équations dans R2 tout système de deux équations de
premier degré de la forme :
Résoudre un système
linéaire de deux équations à deux inconnues dans IRXIR revient à déterminer les
couples (x,y) solution
de ce système, La résolution d’un tel système se fait
par substitution ou par combinaison linéaire.
a) Méthode par substitution
On procède comme suit :
Dans
l’une des équations, on exprime l’une des inconnues en fonction de la deuxième.
On
remplace dans l’autre équation cette inconnue par son expression déterminée
plus.
haut, puis on résout cette équation à une inconnue pour trouver la valeur de la
deuxième inconnue.
On
remplace cette deuxième inconnue par sa valeur dans l’expression de la première
afin de trouver aussi la valeur de la première inconnue.
Exemple : Résoudre dans IR
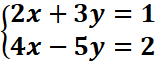
Résolution :
De la
première équation :2x+3y=1 => y=(1-2x)/3
On remplace
y par cette expression dans la deuxième équation
< = > 4x-5((1-2x) /3) =2
<
= > 4x – 5/3+10x/3 =2
<
= > 22x/3=11/3
=> x=11/22=1/2
On peut trouver y en remplaçant x par
y=(1-2x)/3y =(1-2(1/2)/3=0
=> S={(1/2,0)}
b) Méthode par combinaison linéaire
Elle consiste à multiplier chacune des
deux équations par des coefficients appropriés de façon
à éliminer une des deux variables et à déterminer l’autre par la
suite.
Exemple : Résoudre dans IR
Multiplions
la première équation par 3 et la seconde par 2, on a :
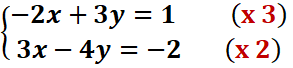
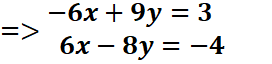
En faisant
l’addition membre à membre, on
obtient :
0x +y= -1=> y=-1
On remplace
x par dans l’une des deux équations :
=> x=-2
S={(-2,-1)}
SYSTEME
D’INEQUATION A UNE INCONNUE
Il s’agit d’un groupe
de plusieurs inéquations ayant la même inconnue. Pour résoudre un tel système,
on résout séparément chaque inéquation puis on fait l’intersection de leurs
différents ensembles solutions pour obtenir la solution du système.
Exemples :
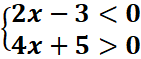
2x-3<0
2x<3
x<3/2 =>S1=]3/2,→]
4x+5≥0
4x≥-5
x≥-5/4 =>S2
=[-5/2,→[
S=S1⋂S2=[-5/4,3/2[
NB :Pour trouver les
intersecions et les reunions des intervalles, on utilise une droite graduee.
EXERCICES
EXERCICE
I: Résoudre par substitution et par combinaison
linéaire les systèmes suivant dans IRxIR:
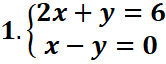
2.
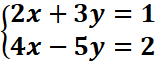
EXERCICE
II: Résoudre
les inéquations suivantes :
1. 
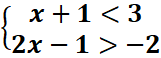
2. 
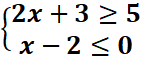
3.
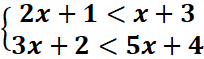
EXERCICE
III :
Situation :
Pendant la période de pénurie de ciment, deux entrepreneurs
A et B achètent ensemble 12 tonnes de ciment. Si on ajoute 3 tonnes de ciment a
la part de A, on obtient le double de la part de B. La masse de sac de ciment
est de 50 kg et le camion ne peut transporter que 500kg.
Taches :
1.Determine en tonnes, la part de ciment de chacun des
entrepreneurs A et B.
2. Sachant qu’une tonne correspond à 1000kg, combien de
sacs de ciment aura chacun des entrepreneurs.
3.Combien de tours fera le camion pour transporter les 12
tonnes de ciment ?
EXERCICE
IV :
Situation :
Un planteur d’arbres
fruitiers achète 76 plants : des manguiers a 1000frs et des avocatiers a
1290frs le plant, sa facture s’élève à 89340 frs. Chaque manguier a produit en
moyenne 50 mangues qu’il a vendu à raison de 50 frs l’une, 70 avocats qu’il a
vendu à raison de 100 frs l’une, avec une perte de 10% d’avocats produits.
Taches :
1.Determiner le nombre de plants de manguiers
et le nombre de plants d’avocatiers achetés par le planteur.
2. A-t-il réalisé un bénéfice sur les
mangues ? Si oui, lequel ?
3. A-t-il réalisé un
bénéfice sur les avocats ? Si oui, lequel ?
CORRIGES
EXERCICE I :
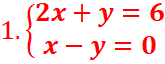
EXERCICE I:
1-par substitution
De la deuxième équation, on a :
x-y=0 => x=y
En remplaçant dans la première équation, on a :
2x+y-6=0 <=>2x+x-6=0
<=>3x-6=0 =>x=2 et y=2
=> S={(2,2)}
-par combinaison linéaire
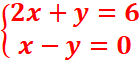
1x(2x+y=6)
-2x(x-y=0) =>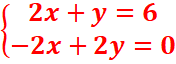
en faisant la somme membre a membre, 0n
a : 0x +3y=6 => y=2
En remplaçant y dans l’une des équations, on a : 2x+y=6 <
=> 2x+2=6 =>x=2
=> S={(2,2)}
2. 
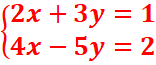
1-par substitution
De la première équation, on a :
2x+3y=1 => y=(1-2x)/3
En remplaçant dans la deuxième équation, on a :
4x-5y=2
< =>4x -5((1-2x)/3)=2
<=>4x -5/3 +10x/3=2
<=>4x +10x/3=2+5/3
<=>22x/3=11/3 =>x=11/22=1/2
y=(1-2x)/3= (1-2.1/2)/3=0
=> S={(1/2,0)}
-par combinaison linéaire
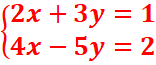
-2x(2x+3y=1)
1x(4x-5y=2) =>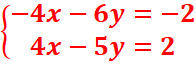
en faisant la somme membre a
membre, 0n a : 0x -11y=0=> y=0
En remplaçant y dans l’une des équations, on a : 2x+y=6 ó2x+0=1 =>x=1/2
=> S={(1/2,0)}
EXERCICE II:
1. 
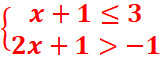
x+1≤3
x≤2
S1=]←,2]
2x+1>-1
2x>-2 x>-1
S2=]-1,→[
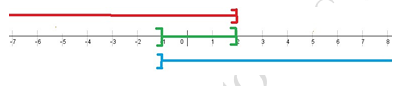
S= S1⋂S2=]-1,2]
2. 
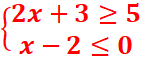
2x+3≥5
x-2≤0
2x>2
x>1=>S1=]1,→[
x≤2
=>S2=]←,2]
S=S1⋂S2=[1,2]
3.
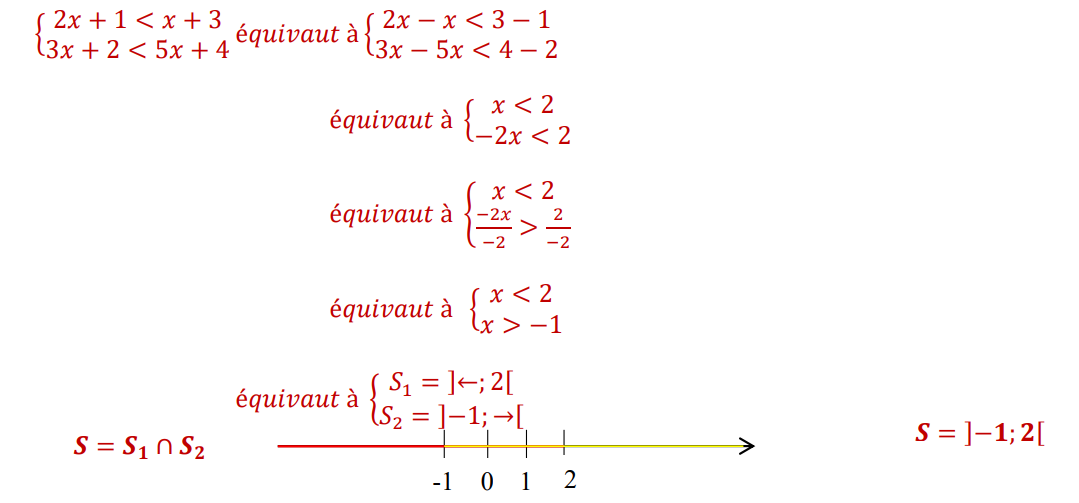
EXERCICE
III :
1.Determinons en tonnes, la part de ciment de chacun des entrepreneurs
A et B.
Soient : x la part de A
y
la part de B
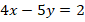
2. Nombre de sacs de ciment aura chacun des entrepreneurs.
A : 5x1000=5000/50=100sacs
B : 7x1000=7000/50=14 sacs
3.Nombre de tours fera le camion pour transporter les 12 tonnes de ciment .
12000/500=24 tours
EXERCICE
IV :
1.Determinons le nombre de plants de manguiers et le nombre de
plants d’avocatiers achetés par le planteur.
x : nombre de manguiers
y :nombre d’avocatiers
2. bénéfice sur
les mangues.
Montant de la vente des mangues :30manguiersx50manguesx50francs=75000frs
Montant d’achat des manguiers :30 plantsx1000francs=30000frs
Bénéfice :75000-30000=45000francs
3. bénéfice sur les avocats.
Nombre d’avocats vendus :(46
avocatiersx70 avocats) - (46 avocatsx70 avocats) x10/100=2898 avocats
disponibles pour la vente.
Montant de la vente des avocats :2898x60francs=173880frs
Montant d’achat des avocatiers 46 plantsx1290francs=59340frs
Bénéfice :173880-59340=114540francs