EQUATIONS ET INEQUATIONS TRIGONOMETRIQUES
EQUATIONS
Equation du type sinx=α
Si α ϵ [-1,1], alors il existe un réel
β tel que sinβ=α
D’où : 
Exemple1 : sinx=-Ѵ2/2
sinx=-Ѵ2/2 <=> sinx=sin5π/4 =>

![]()

![]()
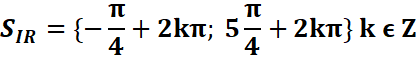
Exemple 2 : sin(x+π)=sin(π/3-2x)
=>
![]()
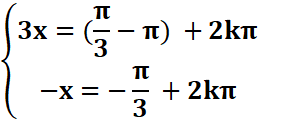
=>
![]()
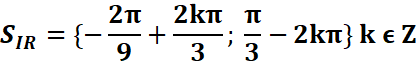
Exemple 3 : sinx=-Ѵ2/2 dans [0,2π]

![]()
Il faut en plus que 0<x<2π donc que
0<5π/4 +2kπ<2π
0<5π/4 +2kπ<2π
-5π/4 < +2kπ<2π
-5π/4=3π/4
-(5/4 )/2<k<3/4)/2=
-0,625<k<0,375
k peut prendre la valeur 0
k=0
x=5π/4 +2(0)π= 5π/4
x=-π/4
+2(0)π=-π/4
S[0,2π] ={ -π/4, 5π/4 }
Equation du type cosx=α
Si α ϵ [-1,1], alors il existe un réel
β tel que cosβ=α
D’où : 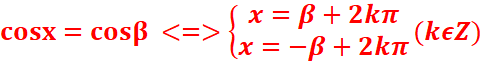
Exemple1 : cosx=1/2
cosx=1/2 <=> cosx=cosπ/3 =>
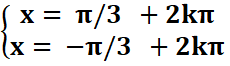
![]()
SIR={![]()
Exemple 2 : cos(2x-π/2)=cos(3x+π)
<=> ou avec kϵZ
=>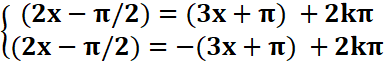
![]()
=>
![]()
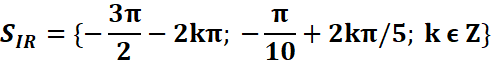
Exemple 3 : cosx=1/2 dans [0,2π]
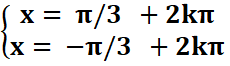
![]()
Il faut en plus que 0<x<2π donc que
0<π/3 +2kπ<2π
0<π/3 +2kπ<2π
0 -π/3 <
+2kπ<2π -π/3=5π/3
(-1/3 )/2<k<(5/3)/2
-0,167<k<1,67
k peut prendre la valeur 0 ,1
k=0 x= π/3 +2(0)π= π/3
x= -π/3
+2(0)π= -π/3 ou 5π/3
k=1 x= π/3 +2(1)π= 7π/3 ou π/3
x=- π/3
+2(1)π= 5π/3
S[0,2π] ={ π/3 , 5π/3 }
Equation du type sinx=cosa
sinx=cosa <=> sinx=sin
(π/2-a) et cosa=cos(π/2-a)
Or sin (π/2-a)=cosa
cos(π/2-x)=sinx
<=> sinx=cosa
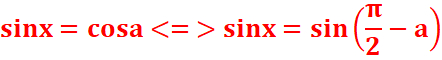
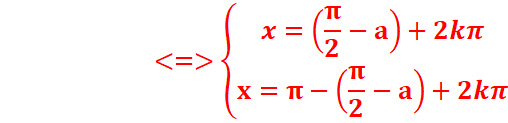
Equation du type tanx=α
Si α ϵIR, il existe un réel β tel que
tanβ=α
![]()
Exemple : tan(x-π/6) =tan(π/4)
x-π/6=π/4 + kπ=>
x=5π/12 +kπ, kϵZ
SIR ={5π/12
+kπ, kϵZ]
Équation du type acosx + bsinx-c=0

Exemple : Résoudre cosx +Ѵ3 sinx=-Ѵ2
![]()
 =>
l’équation admet des solutions réelles,
=>
l’équation admet des solutions réelles,
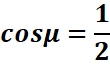
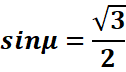
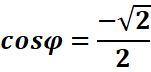
![]() =-
=-![]()
![]()
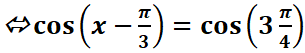
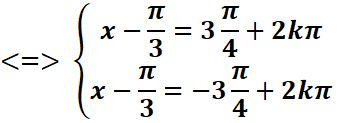
=>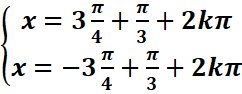
=>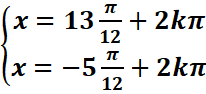 avec kϵZ
avec kϵZ
SIR={![]() }
}![]() kϵZ
kϵZ
INEQUATIONS TRIGONOMETRIQUES
Inéquation du type sinx <b, sinx ≥b
:
Exemple 1 : sinx ≤ 1/2
sinx=1/2 < =>sinx=sinπ/6
=>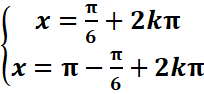
=>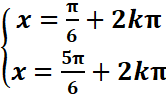
1ere
méthode : utiliser le cercle trigonométrique
On place sur
le cercle trigonométrique les images de ces solutions.
Les points
dont les images ont pour abscisses sont les points appartenant à l’arc orienté
en rouge sur la figure ci-dessous,
donc si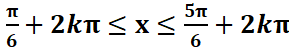
En tournant
toujours dans le sens mathématique positif et en notant les solutions sur le
premier tour de cercle, nous lisons sur le graphique :
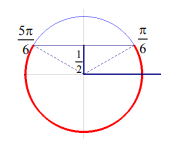
·
Dans
l’intervalle] -π,π] =>
S] -π,π]
= ]- π,π/6] U
[5π/6, π]
·
Dans
l’intervalle [0,2π[ =>
S] 0,2π] =[0,π/6] U [5π/6,2π[
2eme méthode : utiliser une fonction
On étudie la courbe f(x)=sinx-1/2 alors f(x)≤0
|
x |
0 Π 5π/6 2π |
|
f(x) |
- 0 + 0 - |
f(π/3)=sin(π/3)
-1/2=Ѵ3/2 -1 ≥0 or π/3 ϵ [ π/6,5π/6]
S[ 0,2π[ =[0,π/6] U [5π/6, 2π[
Inéquation du type cosx < a, cosx ≥
a
Exemple : cosx ≤ -Ѵ2/2
cosx=cos3π/4 <=
>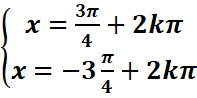
On place sur le cercle trigonométrique les images de
ces solutions.
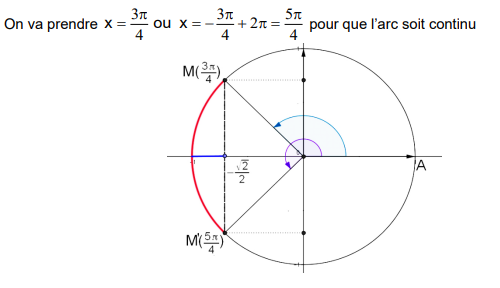
Les points dont les images ont pour abscisses les
points appartenant à l’arc orienté MM’, donc si
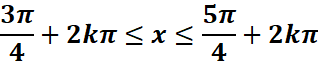
L’ensemble des solutions est donc la réunion de tous
les intervalles de la forme
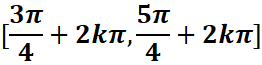
où k est un
entier relatif.
Inéquation du type tan<a, tanx ≥ b
Exemple : tan(3x+π/2)>Ѵ3
tan(3x+π/2)=Ѵ3
=tanπ/3 < =>(3x+π/2)= π/3
+kπ
< =>(3x) = π/3-π/2 +kπ
=>x=-π/18 +kπ/3
D’après le graphique :
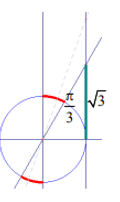
SIR=]-π/18
+kπ/3,0[
EXERCICES
EXERCICE
I :
1. Résoudre :
a. cosx = -Ѵ3/2
b.Ѵ3cosx-3sinx = 3
2.On
considère un nombre réel x de l’intervalle [0,π/2]
tel que sinx=1/4
a- Déterminer la valeur exacte de
cosx
b-Déterminer avec la calculatrice en
mode radian, une valeur approchée de x au millième près.
c- Vérifier à l’aide de la
calculatrice la valeur obtenue en a.
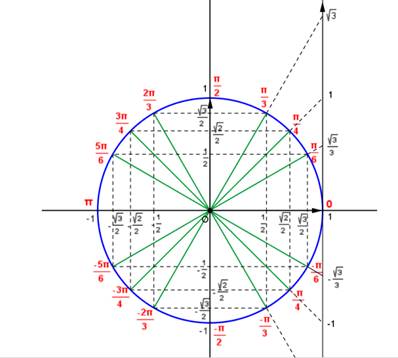
3.Utiliser
le cercle trigonométrique ci-dessous pour déterminer l’ensemble des solutions
des équations :
a. cosx=-1/2 dans [0,π]
b. sinx=-![]() /2 dans[-π/2,π/2]
/2 dans[-π/2,π/2]
c. 1-cos3x=0
dans [-π,π]
EXERCICE
II : Résoudre
dans l’intervalle I les inéquations suivantes :
1.2sinx-Ѵ3 ≥
0 I= IR
2.cos(x-π/3) ≥ Ѵ3/2 I= IR
3. sinx ≥ 1/2 I= ] -π, π] ; I= ] 0,2π]; I= IR
4. sin2x ≤ 1/2 I= ] -π, π] ; I= ] 0,2π]; I= IR
5. cosx ≤ Ѵ2/2 I= ] -π, π] ; I= ] 0,2π]
EXERCICE III:
1.
Développer cos(x+y) + cos(x-y)
2.Resoudre
dans IR le système :
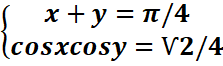
EXERCICE IV:
1.a)
calculer (Ѵ2 +1)2
b) résoudre dans [0,2π]
l’équation : 2cos2x + (Ѵ2 -1)cosx-Ѵ2/2=0
2. résoudre
dans [0,2π] l’inéquation : 2cos2x + (Ѵ2 -1)cosx-Ѵ2/2≥0
CORRIGES
EXERCICE I :
1.a.
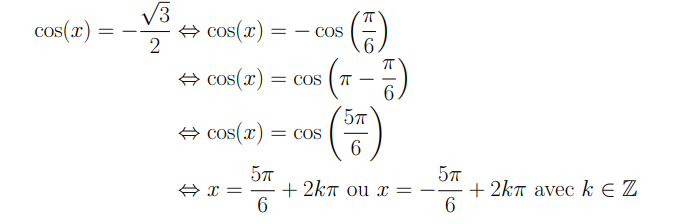
b. Ѵ3cosx-3sinx=3
![]() =2Ѵ3
=2Ѵ3
 => l’équation admet des solutions
réelles,
=> l’équation admet des solutions
réelles,
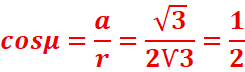
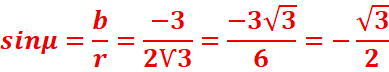
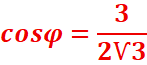
![]() =
=![]()
![]()
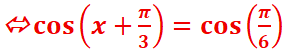
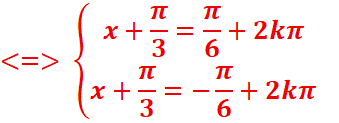
=> avec kϵZ
avec kϵZ
![]() {
{![]() }
}![]() kϵZ
kϵZ
// Ѵ3cosx-3sinx=3 <=> cosx-Ѵ3sinx=Ѵ3
<=>
cosx-tanπ/3sinx=Ѵ3
<=>cosπ/3 cosx-sinπ/3sinx=Ѵ3
<=> cos(x+π/3)=Ѵ3/2
<=> cos(x+π/3)=cosπ/6
2.a-

3.Utiliser
le cercle trigonométrique ci-dessous pour déterminer l’ensemble des solutions
des équations :
a. cosx=-1/2 dans [0,π]
b. sinx=-![]() /2 dans[-π/2,π/2]
/2 dans[-π/2,π/2]
c. 1-cos3x=0
dans [-π,π]
3.a-

b-

c-
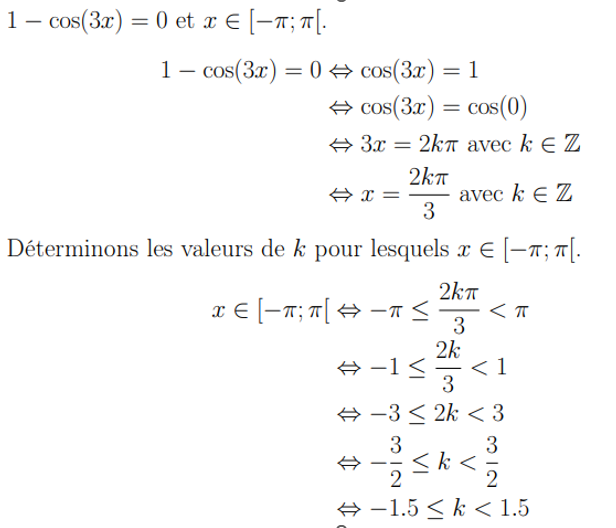
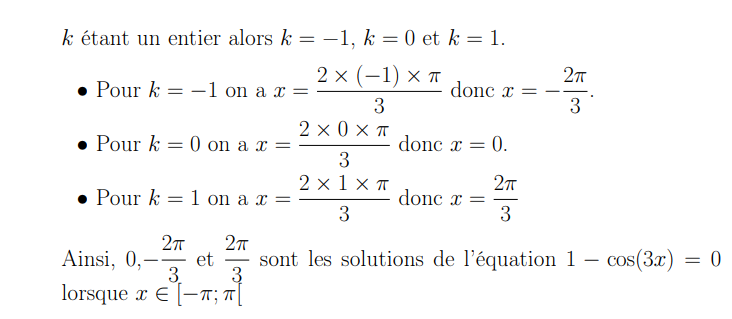
EXERCICE II :
1. 2sinx-Ѵ3≥0
2sinx-Ѵ3=0 <= >sinx=Ѵ3/2=sinπ/3 => kϵZ
kϵZ
D’après le graphique :
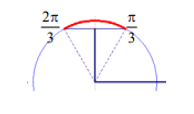
S=[π/3![]() ,2π/3
,2π/3 ![]() kϵZ
kϵZ
2. cos(x-π/3) ≥Ѵ3/2
cos(x-π/3)=Ѵ3/2=cosπ/6 => 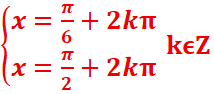
S=[π/6![]() ,π/2
,π/2 ![]() kϵZ ]
kϵZ ]
3. sinx≥1/2
sinx=1/2 < =>sinx=sinπ/6 =>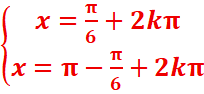
=>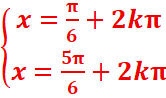
Dans l’intervalle] -π, π]
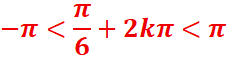
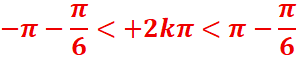
-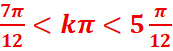
![]()
k peut prendre le
valeurs 0
k=0 ![]()
![]()
S] -π,π] = [π/6,5π/6]
Dans l’intervalle] 0,2π]
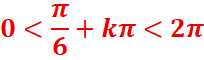
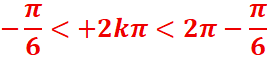
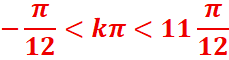
![]()
k peut prendre le
valeurs 0
k=0 x = ![]()
x=![]()
L’arc qui va de π/6 a 5π/6 comprend tous les points solution de cette
inéquation.
S[0,2π] =[ π/6,5π/6]
Dans IR
L’ensemble des solutions dans IR est la réunion des intervalles de la
forme [ ![]() ,
, ![]() ]
]
4. sin2x ≤ 1/2
sin2x=sin(π/6)
<=> kϵZ
kϵZ
<=>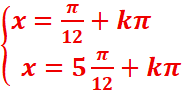 kϵZ
kϵZ
Dans l’intervalle] -π,π]
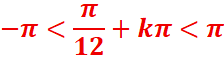
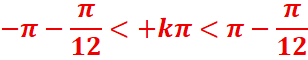
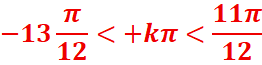
![]()
k peut prendre la
valeur 0
k=0 x=-![]()
![]()
S] -π,π] = ]-
π,π/12] U [5π/12, π]
Dans l’intervalle] 0,2π]
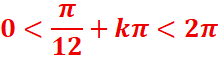
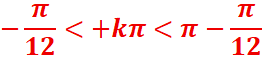
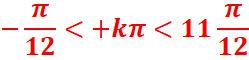
![]()
k peut prendre la
valeur 0
k=0 x = ![]()
x=![]()
S] 0,2π] =[0,π/12] U [5π/12,2π[
Dans IR
L’ensemble des solutions dans IR est la
réunion des intervalles de la forme] ![]() ,
, ![]()
5. cosx ≤Ѵ2/2
Dans l’intervalle] -π, π]
=>S] -π,π] =]-π,-π/4]U[π/4,π]
Dans l’intervalle [0,2π[
=>S[ 0,2π[ =[π/4,7π/4]
EXERCICE III:
1.
cos(x+y) + cos(x-y) =cosxcosy-sinxsiny+cosxcosy+sinxsiny=2 cosxcosy
2.resoudre dans IR le système :
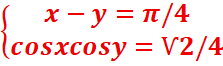
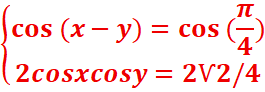
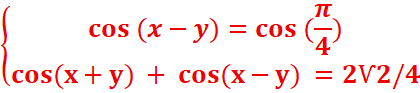
 =>
=> 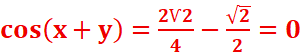
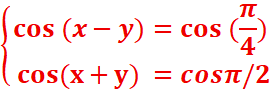
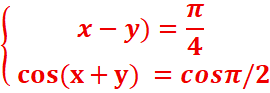
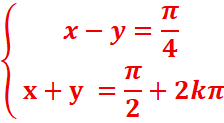
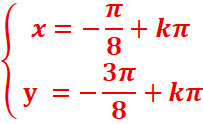
EXERCICE IV:
1.a) calcul de (Ѵ2 +1)2
(Ѵ2 +1)(Ѵ2
+1)=3+2Ѵ2
b) Equation : 2cos2x + (Ѵ2
-1)cosx-Ѵ2/2=0 dans [0,2π]
posons X=cosx
L’équation devient : X2+(Ѵ2
-1)X- Ѵ2/2=0
Δ=(Ѵ2
-1)2-4(2)(- Ѵ2/2)=3+2Ѵ2=(Ѵ2 +1)2
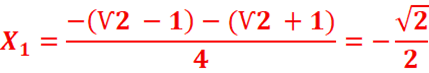
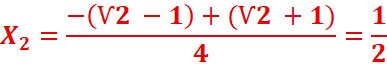
· 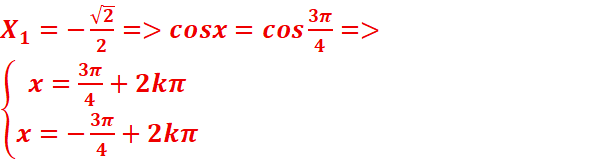
Dans [0,2π]
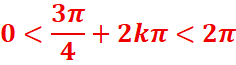
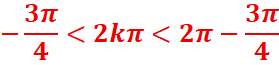
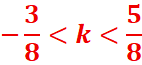
-0,375<k<0.625
k=0 =>x=![]()
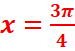
Dans [0,2π]
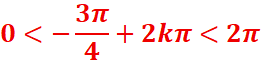
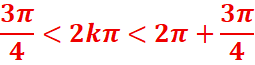
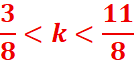
0,375<k<1,3
K=1 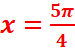
· 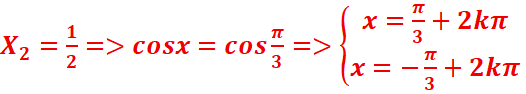
Dans [0,2π]
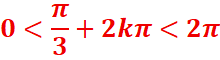
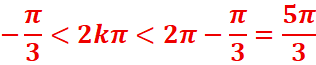
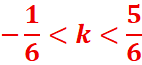
-0,16<k<0,83
k=0 =>![]()
Dans [0,2π]
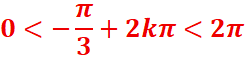
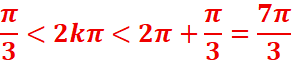
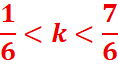
0,16<k<1,16
k=1 =>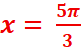
S[0.2π] =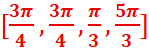
2. résoudre dans [0,2π]
l’inéquation : 2cos2x + (Ѵ2 -1)cosx-Ѵ2/2
≥0
Soit f(x)= : 2cos2x + (Ѵ2
-1)cosx-Ѵ2/2 ≥0
|
x |
0 π/3 3π/4 5π/4 5π/3 2π |
||||
|
cosx-1/2 |
+ |
- |
- |
- |
+ |
|
cosx+Ѵ2/2 |
+ |
+ |
- |
+ |
+ |
|
f(x) |
+ |
- |
+ |
- |
+ |
f(3π/4)=cos(3π/4)-1/2=- Ѵ2/2
-1/2 <0
f(π/3)=cos(π/3)+ Ѵ2/2 =1/2+
Ѵ2/2 >0
S[0,2π] =[0, π/3] U [ 3π/4, 5π/4] U [ 5π/3,2π[
Avez-vous
un exercice à proposer ?Cliquez-ici
Merci de votre visite
Laissez un commentaire