ÉQUATIONS ET INEQUATIONS
ÉQUATIONS
Ø Une
équation de premier degré d’inconnue x dans IR est une égalité
entre deux polynômes du premier degré ou alors entre un polynôme de premier
degré et 0.
Ø Résoudre une équation de premier degré dans IR
revient à déterminer les valeurs pouvant être prises par l’inconnue x et de
les regrouper dans un ensemble appelé ensemble solution et généralement
noté S.
EQUATION
DE LA FORME x +a = b
Ø Dans une équation, lorsqu’un terme change
de membre (traverse l’égalité), alors le signe de ce terme change aussi
:
x+b=0 => x=b-a
L’ensemble des solutions est S={b-a}
Exemple : Résoudre dans
IR : x+ 4= 𝟕 et x-3=10
x+4=7 <= >x=7-4=3
x-3=10 <= >x=10+3=13
EQUATION
DE LA FORME ax
= b
Ø Pour deux réels donnés a 𝒆t b avec a ≠ 𝟎 ;
L’équation ax = b équivaut à x =b/a
S=
{b/a }
Exemple
Résoudre dans IR : - 6x = 3 => 
-
S ={-1/2}
EQUATION DE
LA FORME ax +b
= 𝒄x + 𝒅
Pour résoudre une telle équation,
Ø On regroupe d’abord les termes contenant l’inconnue d’un côté de
l’égalité (de préférence du côté gauche) et les termes constants (sans
inconnue) dans l’autre côté de l’égalité en prenant soin de changer le signe
des termes qui traversent l’égalité.
Ø On réduit ensuite l’équation obtenue, jusqu’à obtenir une
équation de la forme ax=b pour avoir x=b/a
Exemple
Résoudre dans IR : 2x
– 3 = 4x + 𝟕 ; - 6x- 𝟗 = x – 6
2x-3=4x+7 <=>2x-4x=7+3
<=>-2x=10 =>x =
10/2=-5
S={-5}
- 6x- 𝟗 = x – 6 < = > -6x-x=-6+9
< = > -7x=3. => x =-7/3
S = {-7/3}
Remarque : Si lors de la
résolution, on obtient
·
0x=0, on a une infinité de
solution : S=IR
·
0x=b avec b non nul, il n’y a pas
de solution : S =ø ou S={ } (ensemble vide)
Exemple : Résoudre dans IR :
(4x-6)/2= 2x-3 ; -x+18=3(x+6)-4x.
(4x-6)/2= 2x-3 <=>4x-6=2(2x-3)
< = >
4x-4x=-6+8
< = >
0x=2 =>S={}
-x+18=3(x+6)-4x. <= > -x+18=3x+18-4x
< = > -x-3x+4x=18-18
< = > 0x=0 => S=IR
EQUATION DE LA FORME (ax +b)(cx+d)=0
Exemple :
Résoudre dans IR :
(2x +1 )(
x- 4) = 𝟎 ; x(-x+5)= 𝟎.
Solution :
(2x +1 )(
x- 4) = 𝟎
<=> 
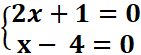
S={-1/2 ;4)
x ( -x+5) =
𝟎
<=> 
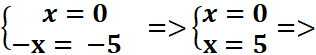S={0 ;5}
EQUATION
DE LA FORME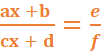 
On a :
f.(ax+b) = e.(cx + d) ,on
revient au cas précédent
Exemple : Résoudre : 
Solution :
2(2x+1)=3(x-2) équivaut à 4x +2=3x-6 équivaut 4x-3x=-6-2 donc x=-8
EQUATION DE LA FORME ax2 +bx+c=0
Utilisation du début du carre
Soit à résoudre l’équation x2+4x-5=0
x2+4x est le début d’un
carré :(x+2)2
or :(x+2)2= x2+4x+4
=> x2+4x=(x+2)2 – 4
donc x2+4x+5=(x+2)2 – 4 -5
x2+4x+5=0 < =>
(x+2)2 – 4 -5=0
< => (x+2)2 –
9 =0
Sachant que :a2 -b2=(a-b)(a+b)
(x+2)2 – 9=[(x+2)-3][(x+2)+3]=0
< =>
(x-1)(x+5)=0 => x=1 ou x=-5
L’expression (x+2)2 – 9 est la forme canonique
NB :En général, p(x)=ax2 +bx c, la forme canonique de p(x)=a[(x+b/2a)2
– Δ/4a2 ]
Δ=b2-4ac est le discriminant
Si x1 et x2
sont deux racines de p(x), on a p(x)=a(x-x1)(x-x2).
C’est la forme factorisée de p(x).
INEQUATIONS DU PREMIER DEGRÉ
Définition
Ø Une inéquation de premier degré dans IR est une inégalité
entre deux polynômes du premier degré ou alors entre un polynôme de premier
degré et 0.
Ø Résoudre dans IR une inéquation de premier degré c’est déterminer
l’ensemble de tous les nombres qui vérifient cette inéquation. Cet ensemble est
appelé ensemble solution noté S et est très souvent un
intervalle ou une réunion d’intervalles.
Inéquation
du type ax+b < cx+d
Pour résoudre ces types d’équations, on renvoi les
termes en x d’un côté de l’inégalité (de préférence du celui de gauche) et les
termes constants de l’autre côté.
Exemple : Résoudre dans IR
2x+5< x +3
<=>2x-x<3-5
<=> x< - 3
=> S=]←,-3[
Remarques
:
Ø
Lorsqu’on multiplie ou divise les deux membres d’une inégalité par
un nombre réel négatif non nul, l’inégalité change de sens.
Ø
Lorsqu’on multiplie ou divise les deux membres d’une inégalité par un nombre
réel positif non nul, l’inégalité ne change pas de sens.
EXERCICES
EXERCICE I : Résoudre dans IR
1. x+15=0
2.2x=6
3.6x-3=2x-2
4.
5. 
EXERCICE II :
1.(2x-1)(-3x+7)=0
2.(x-3)(2x-7)-(4x-2)(x-3)+(5x+7)(x-3)=0
3.x(x-2)+x2-4-(x-2)(2x+1)
4. 
5. 
EXERCICE III : résoudre p(x)=0
1. p(x)=x2 +2x -3
2. p(x)=x2 +12x + 35
3.p(x)=4x2 -12x+8
EXERCICE IV : Résoudre dans. IR les inéquations
suivantes :
1. 5x+3<2x-6
2. 2x-1 ≥
x+2
3.
x+6 ≥3x
4.
-2x+5>x-1
EXERCICE V : Résoudre dans. IR les
inéquations suivantes :
1. -3x + 1> x+3
2. 2(3x-1) + 3(x-1)≥0
EXERCICE VI :
Amadou dispose d’une somme de 8 000 FCFA pour l’achat de ses fournitures scolaires pour le compte de l’année scolaire 2020/2021. Pour cela, il achète du matériel de géométrie à 4 000 FCFA et un certain nombre de cahiers de 200 pages qui coute 400 FCFA l’unité. IL aimerait connaitre le nombre de cahiers qu’il peut acheter. Aide Amadou à trouver ce nombre.
EXERCICE VII :
Situation :
Anna a reçu de son oncle de
l’argent. Sa mère lui propose de prendre cet argent pour placer dans sa réunion
à un taux d’intérêt mensuel de 10% pendant 03 mois, proposition refusée par
Anna. Elle préfère utiliser une partie de cet argent et fructifier l’autre
partie. Elle entre dans un supermarché avec cet argent pour faire des achats.
Elle utilise le quart de cette somme pour acheter des ustensiles de cuisine, le
tiers du reste pour acheter les produits de beauté qu’elle pourra revendre.
Elle règle également une dette dont le montant correspond à 25% du montant de
la somme initiale et elle rentre avec 8000F.
Taches :
1-Quel est le montant de la somme
initiale qu’Anna possédait avant d’entrer dans le supermarché ?
2-En supposant que le montant de la
somme initiale était 32000F. Quel bénéfice obtiendrait Anita si elle vendait
les produits de beauté à 12000F pendant le même temps ?
3-. Anna avait-elle raison de
refuser la proposition de sa mère ?
CORRIGES
EXERCICE I.
1.
x+15=0 <= >x=-15 =>S={-15}
2.2x=6 <= >x=6/2=3
3.6x-3=2x-2<= >6x-2x=-2+3<= >4x=1 =>x=1/4
4. condition
d’existence :x-1≠1=> x≠1
x+1=1.(x-1)
x-x=-1-1.
x=-2
5.condition
d’existence :2x-1≠0 =>x≠1/2
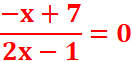
ð S={7}
EXERCICE II :
1.(2x-1)(-3x+7)=0
=>
S={1/2,7/3}
2.(x-3)(2x-7)-(4x-2)(x-3)+(5x+7)(x-3)=0 <=
>(x-3)[(2x-7)-(4x-2)+(5x+7)]=0
<= >(x-3)[2x-7-4x+2+5x+7]=0
<= >(x-3)[3x+2]=0 =>
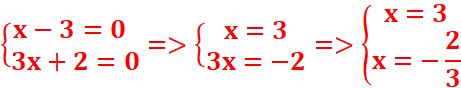
S={3,-2/3}
3.x(x-2)+x2-4-(x-2)(2x+1)=0 <=
>(x-2)[x+(x+2)-(2x+1)]=0
<= >(x-2)[x+x+2-2x-1]=0
<= >(x-2)=0
=>S={2}
4. condition d’existence :2x-1≠0
=>x≠1/2
<=>5(-x +7)=4(2x-1)
<=>(-5x +35)=(8x-4)
<=>(-5x -8x)=(-4-35)
<=> -13x=-39 =>x=39/3=13
S={13}
5. condition d’existence :x-1≠1=> x≠1
<=>-x
+1=2(x-1)
<=>-x +1= -2x+2
<=>x=1
S={ }
EXERCICE III :
1. p(x)=x2 +2x -3
p(x)=x2
+2x -3=(x+2/2)2 –(2/2)2-3=(x+1)2 – 4
p(x)=0
<= >(x+1)2 – 4=0
<= >[(x+1) – 2][ (x+1) + 2]=0
<= >[x – 1][ x+3 ]=0 => x=1ou x=-3
2. p(x)=x2 +12x + 35
p(x)=x2
+12x + 35=(x+12/2)2-(12/2)2 +35=(x+6)2-(6)2 +35==(x+6)2-1
p(x)=0
<= >(x+6)2 – 1=0
<= >[(x+6) – 1][ (x+6) + 1]=0
<= >[x +5][ x+7 ]=0 => x=-5 ou x=-7
3.p(x)=4x2 -12x+8
p(x)=4x2
-12x + 8=4(x2-3x+8/4)=4[(x-3/2)2-(3/2)2 +2]=(x-3/2)2-(3/2)2 +2]=4[(x-3/2)2-1/4]
p(x)=0
<= >4[(x-3/2)2 – 1/4]=0
<= >[(x-3/2) – 1/2][ (x-3/2) +
1/2]=0
<= >[x -2][ x+1 ]=0 => x=2 ou x=-1
EXERCICE
IV : Résoudre dans. IR les
inéquations suivantes :
1. 5x+3<2x-6 <=> 5x-2x<-6-3
<=>3x<-9
<=>x<-9/3
=-3 => S=]←,-3[
2. 2x -1≥ x+2 <=>2x-x ≥
2+1
<=>x
=>S=[3 ;⇀[
3.
x+6 ≥3x <=>x-3x ≥ -6
<=>-2x≥-6
<=>-x≥-3
<=>x≤3
=>S=]
4.
-2x+5 > x-1 <=>-2x-x>-1-5
<=>-3x>-6
<=>x<2 => S=]←,2[
EXERCICE
V : Résoudre dans. IR les
inéquations suivantes :
1. -3x + 1>
x+3 <=>-3x-x>3-1
<=>-4x>2 =>x<-1/2
et S=]←,-1/2[
2. 2(3x-1) + 3(x-1)≥0 <=> 6x-2 +3x-3≥0
<=>9x≥5 =>x≥5/9 et S= S=[5/9,→[
EXERCICE III.
Soit x le nombre de cahier de 200pages, on a :
8000=4000 +400x < = > 400x=4000
=>x=4000/400=10 cahiers.
EXERCICE IV.
1)soit x cette somme
d’argent
Achat des ustensiles de
cuisine :( 1/4) x
(Reste :x-( 1/4) x)
Achat des produits de
beauté : tiers du reste 
(x-( 1/4) x)
Dette : 25% x
Reste : 8000
(
+
< = >3x=8000.12< =
>3x=96000=>x=32000
2. montant d’achat des produits de beauté :
Bénéfice :12000-8000=4000frs
3.
Proposition de sa mère :
Intérêt :32000x10/100=3200frs
x 3mois=9600frs >4000frs
Elle n’a
pas eu raison de refuser l’offre de sa mère.