EQUATIONS DIFFÉRENTIELLES

Notion d’équations différentielles

On appelle équation différentielle, toute équation ayant pour inconnue une fonction, dans laquelle figure au moins une des dérivées successives de la fonction inconnue.

· Lorsque le plus grand ordre des dérivées intervenant est n, n étant un entier naturel, l’équation différentielle est dite d’ordre n.

· Toute fonction vérifiant une équation différentielle sur un intervalle I ouvert est appelée solution sur I de cette équation différentielle.

Exemples :

· f’ +3f =0 est une équation différentielle de degré1 ou d’ordre 1.

· 3g ‘’ -2g’ +6g=0 est une équation différentielle de degré 2 ou d’ordre 2.

Equation différentielle du type f’ +af =0

On appelle équation différentielle du premier ordre a coefficients constants sans second membre, toute équation différentielle qui peut s’écrire sous la forme

f’ +af =0.

Les solutions sur l’ensemble des nombres réels de cette équation différentielle sont des fonctions de la forme ke^-ax avec k et a des nombres réels.

Exercice d’application :

On donne l’équation différentielle(E) : f’-4f=0

Vérifier que e^4x et ke^4x sont solution de cette équation. k réel

Resolution: f(x)=e^4x

f’(x)= (e^4x) ’= 4 e^4x

On a : f’-4f=4 e^4x-4 e^4x=0 donc e^4x bien solution de l’équation E

Equation différentielle du type f’’ +af’ +bf =0

On appelle équation différentielle du second ordre a coefficients constants sans second membre, toute équation différentielle qui peut s’écrire : f’’ +af’ +bf =0

a et b étant des réels.

Equation caractéristique

On appelle équation caractéristique de l’équation différentielle f’’ +af’ +bf =0

(a, b étant des réels) l’équation d’inconnue r tel que: r²+ar+b=0

Exemple :

L’équation différentielle f‘’-2f’+5f=0 f a pour équation caractéristique : r²-2r+5=0

Résolution de l’équation différentielle

Ø L’équation caractéristique admet deux solutions réelles.

Propriété :

(E) est l’équation f’’ +af’ +bf =0, a et b étant des réels

Si l’équation caractéristique de (E) admet deux solutions réelles r₁ et r₂, alors les seules solutions de cette équation différentielle sont les fonctions :

f(x)=Ae^r1x + Be^r2x,

A et B étant des réels

Exemple :

Résolvons f’’ - 4f’ +3f =0

L’équation caractéristique est r²-4r+3=0, admet pour solutions réelles 1 et 3.

Les solutions de cette équation différentielle sont les fonctions :

f(x)= Ae^x + Be^3x, A et B étant des réels

Cas particulier ;

L’équation différentielle f’’- ω²f =0 a pour solutions :

f(x)= Ae^ωx +Be^-ωx

Exemple :

Résolvons f’’ - 9f =0

L’équation caractéristique est r²-9=0, admet pour solutions réelle 3.

Les solutions de cette équation différentielle sont les fonctions :

f(x)= Ae^3x +Be^-3x , A et B étant des réels.

Ø L’équation caractéristique admet une solution unique

Propriété :

(E) est l’équation f’’ +af’ +bf =0, a, b étant des réels

Si l’équation caractéristique de (E) admet une solutions réelle unique r, alors les solutions de cette équation différentielle sont les fonctions :

f(x)= (Ax + B)e^rx ,

A et B étant des réels

Exemple :

Résolvons f’’ - 4f’ +4f =0

L’équation caractéristique est r²-4r+4=0, admet pour solution réelle 2.

Les solutions de cette équation différentielle sont les fonctions :

f(x)= (Ax + B)e^2x , A et B étant des réels

Ø L’équation caractéristique admet deux solutions complexes

Propriété :

(E) est l’équation f’’ +af’ +bf =0, a et b étant des réels

Si l’équation caractéristique de (E) admet deux solutions complexes conjuguées α+iβ et α-iβ, alors les seules de cette équation différentielle sont les fonctions :

f(x)= (A cosβx + Bsinβx)e^αx,

A et B étant des réels.

Exemple :

Résolvons f’’ +f’ +f =0

L’équation caractéristique est r²+r+1=0, admet pour solutions réelles -1/2 +Ѵ3/2 et -1/2-Ѵ3/2.

Les solutions de cette équation différentielle sont les fonctions :

f(x) = (AcosѴ3/2 x +B sin Ѵ3/2 x)e^{-1/2 x}, A et B étant des réels.

Cas particulier :

L’équation différentielle f’’+ ω²f=0 a pour solution :

f(x)= Acosωx + B sinωx,

A et B étant des réels

Exemple :

Résolvons f’’ + 25f =0

L’équation caractéristique est r² + 25=0, admet deux solutions complexes conjuguées 5i et -5i..

Les solutions de cette équation différentielle sont les fonctions :

f(x)= (Acos5 x +B sin5x)e^x, A et B étant des réels.

Tableau récapitulatif :

Equation différentielle du type f’’ +af’ +bf =0

L’équation caractéristique est : r²+ar+b=0

Solution vérifiant une condition initiale

Propriété :

Pour tout triplet (x₀, yo, z₀) de nombres réels, l’équation différentielle

f’’ +af’ +bf =0 admet une unique solution sur IR telle que f(x₀)=y₀ et f’(x₀)=z₀

Exemple :

Résolvons l’équation différentielle : f’’ +4f’ +7f =0

Avec les conditions initiales f(0)=0 et f’(0)=1

L’équation caractéristique est r²+4r+7=0, admet pour solutions complexes -2 +iѴ3 et -2-iѴ3

Les solutions de cette équation différentielle sont les fonctions :

f_AB(x)=(A cosѴ3x + BsinѴ3x)e^-2x

f_AB(0)=0 <=> (Acos0 +B sin 0)e⁰=0 =>, A=0

f’_AB(x)=1 <=> -2A +Ѵ3B=1 =>B=1/Ѵ3 =>f(x)=1/Ѵ3 e^-2x sinѴ3x

Equation du type f’’ +af’ +bf =d (1) ou d est une constante

Pour résoudre une telle équation, on procède comme suit :

a) Rechercher une solution particulière g(x)=a

b) Résoudre l’équation homogène f’’ +af’ +bf =0 (2)

c) Prouver qu’une fonction h est solution de (1) si et seulement si h-g est solution de (2)

d) Solution quelconque de (2) + solution particulière de (1) = solution quelconque de (1)

Exemple :

Résolvons f’’ -4f+4f=0 avec les conditions initiales f(0)=1 et f’(0)=0

L’équation caractéristique est : r²-4r+4=0

Elle admet une unique solution réelle r=2

Les solutions de l’équation déférentielle sont donc les onctions f définies par :

f(x)=(Ax +B)e^2x

Cherchons celle qui vérifie les conditions initiales f(0)=1 et f’(0)=0

Elle vérifie le système A+2B=0 et B=1. = >A=-2 et B=1

Les solutions de l’équation déférentielle sont : f(x) = (-2x +1)e^2x

EXERCICES

EXERCICE I: Résoudre les équations différentielles suivantes

1. f’+3f=0 avec f(0)=1

2. f’’ – 3f’ -4f =0 avec f(0)=1 et f’(0)=4

3.f’’ + 12/5f’ +36/25f=0

4.f’’- 4f’ + 4f=0 avec f(0)=1 et f’(0)=0

5.

EXERCICE II:

En 1990, la population du Benin était d’environ 4 750 000 habitants et d’environ 5 500 000 en 1995.On suppose que la vitesse d’accroissement h’(t) de cette population a l’instant t est proportionnelle au nombre h(t) d’habitants à cet instant.

Tache 1 : Etablir la relation entre le nombre d’habitants h(t) et la vitesse d’accroissement h’(t).

Tache 2 : Etablir la relation entre le nombre d’habitants h(t) et le temps t

Tache 3 : Déterminer en quelle année la population du Benin sera-t-elle de 10 000 000 d’habitants ? de 20 000 000 d’habitants ?

EXERCICE III:

Soit un dipôle RC formé par l’association en série d’un condensateur de capacite C et d’un résistor de résistance R.

q étant la valeur absolue de la charge des armatures du condensateur de capacite C, La charge q acquise par l’armature supérieure est : q = CU

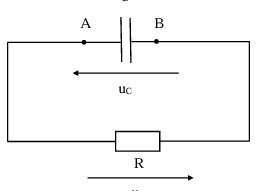
Lorsque le générateur délivre une tension positive u, la tension u_C aux bornes du condensateur augmente jusqu’à la valeur maximale u_Cmax=E : on dit que le condensateur se charge. Pendant les phases ou le générateur délivre une tension nulle, la tension u_C décroît, puis s’annule : le condensateur se décharge.

Tache 1 : Quelle est la relation entre l’intensité i(t) et la charge q(t) ?

Tache 2 : Etablir l’équation qui traduit l’évolution de la charge aux bornes de R

Tache 3 : Calculer la valeur de la charge au bout de t=3 avec RC, q₀=1C.

CORRIGES

EXERCICE I:

1. Les solutions sur l’ensemble des nombres réels de cette équation différentielle sont des fonctions de la forme ke^-3x avec k et a des nombres réels

f(0)=1 <=>ke^-3x0=1 =>k=1

f(x)=e^-3x est une solution

vérification :

f’(x)= -4e^-4x

f’+4f=-4e^-4x+ 4e^-4x=0

2.

L’équation caractéristique est r²-4r-4=0, admet pour solutions réelles -1 et 4.

Les solutions de cette équation différentielle sont les fonctions :

x→ Ae-^x + Be^4x, A et B étant des réels

f(0)=0 <=>A+B=0

f’(0)=4 <=>-A+4B=4 =>B=1 et A=0 donc f(x)= e^4x est une solution.

3.

L’équation caractéristique est r² +12/5 r+36/25=0, admet pour solution réelle -6/5.

les solutions de cette équation différentielle sont les fonctions :

x→(Ax + B)e^{-6/5 x} , A et B étant des réels.

4. Résolvons f’’ - 4f’ +4f =0

L’équation caractéristique est r²-4r+4=0, admet pour solution réelle 2.

les solutions de cette équation différentielle sont les fonctions :

f_AB(x) =(Ax + B)e^2x , A et B étant des réels

f_AB(0)=1 <=> B=1

f’_AB(0)=0 <=>A +2B=0 =>A=-2

f_AB(x) =(-2x + 1)e^2x

EXERCICE II:

Tache 1 : la vitesse d’accroissement h’(t) de cette population a l’instant t est proportionnelle au nombre h(t) d’habitants à cet instant donc h’(t)=ah(t), a reel.

Tache 2 : Cette équation est du type h’- ah=0 donc admet pour solution h(t)=ke^at. Reste à déterminer k et a avec les conditions initiales.

En 1990, 4 750 000=ke^1990a

En1995, 5 500 000=ke^1995a

d’où c’est-a-dire

5a=ln550/475 =>a=0,03

Par la suite, h(t)=5500000e^0,03(t-1995)

Tache 3 : Déterminons en quelle année la population du Benin sera de 10 000 000 d’habitants 

10000000=5 500 000 e^{0,03(t-1995 )} <=>ln100/55=0,03(t-1995 ) => t=2015

Déterminons en quelle année la population du Benin sera de de 20 000 000 d’habitants 

20000000=5 500 000 e^{0,03(t-1995 )}=> t=2039

EXERCICE III:

Tache 1 :

Désignons par q₀ la charge du condensateur a l’instant initial ou commence la décharge, l’intensité i₀ du courant dans le circuit étant nulle. A un instant quelconque, on a

est la tension aux bornes du condensateur

Tache 2 :

La loi d’Ohm aux bornes du résistor est :

Tache 3 :

On obtient l’équation différentielle du type :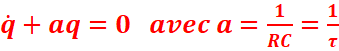

Les solutions sont de la forme :q=ke-^at

A t=0, q=q₀ <=> q₀=ke⁰=> k=q_o d’où la relation q=q₀e-^at

A t=3 q=q₀e^at=e-³=0,05C

Avez-vous un exercice à proposer ? Cliquez-ici

Merci de votre visite
Laissez un commentaire