ANGLES ORIENTES ET TRIGONOMETRIE

ANGLES ORIENTES

Définition

Un angle orienté est défini par deux vecteurs et , noté , . L’angle est alors orienté de vers .

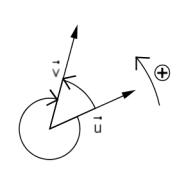
Sur la figure ci-dessous, on a représenté deux angles orientés, représentant le même angle , . Le premier est orienté dans le sens direct et l’autre dans le sens indirect. Le sens direct est le sens contraire aux aiguilles d’une montre.

Propriétés

1) Les vecteurs et , sont colinéaires si et seulement si :

, ou ,

2)Relation de Chasles : Soit trois vecteurs , , alors : , + , = ,

3) Soit les vecteurs et , alors on a :

, = - ,

, , +π

, ,

, = ,

Mesure d’un angle orienté

Un cercle trigonométrique est un cercle de rayon 1.

Soit M et N deux points d’un cercle trigonométrique. M est l’image du réel α, N est l’image du réel b.

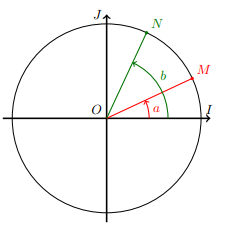
On appelle mesure d’un angle orienté le nombre réel qui quantifie la rotation nécessaire pour amener le cote initial sur le cote final.

Exemple : α est la mesure de l’angle orienté , on note ,

b est la mesure de l’angle orienté , on note ,

La mesure d’un angle orienté s’exprime en radians(rad) ou en degré (°). Un tour complet correspond à 2π radians.

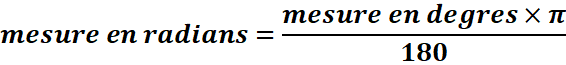
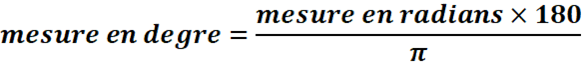
Mesure principale d’un angle orienté.

Un angle orienté peut avoir une infinité de mesures, qui différent d’un entier multiple de 2π. Une seule de ces mesures appartient à l’intervalle] -π, π] : c’est la mesure principale de cet angle orienté.

Ainsi, si β est une mesure de l’angle orienté , d’angle principal α, alors :

β = α+ 2kπ avec k ϵ Z et α ϵ ]-π,π]

Exemple :

13π/6 = π/6 +2π donc π/6 est la mesure principale de l’angle orienté de mesure 13π/6,

Soit , un angle orienté et α sa mesure principale α ϵ ]-π,π]. La mesure de l’angle orienté , est tout nombre réel non nul de la forme (α+2kπ, kϵZ).

On dit que les mesures (en radian) θ₁ et θ₂ d’un même angle orienté , sont égales modulo 2π, s’il existe un entier relatif k tel que :

θ₂ = θ₁ + 2kπ, kϵZ

On écrira alors : θ₁ = θ₂ [2π] qui se lit « θ₁ égale à θ₂ modulo 2π »

Exemple :

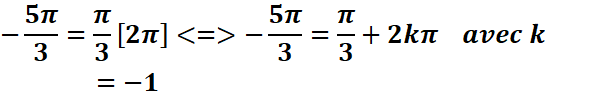
Détermination de la mesure principale d’un angle orienté

On rappelle qu’il existe plusieurs mesures d’un angle orienté dont une seule appartient à l’intervalle] -π, π], la mesure principale de l’angle orienté , .

Dans l’exemple ci-dessus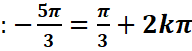

…..

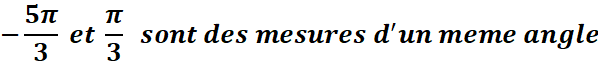
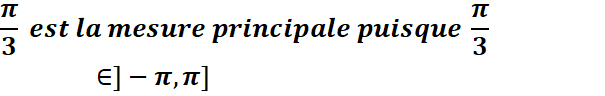
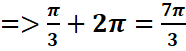
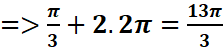
Exemple : Déterminons la mesure principale de l’angle β=24π/5

1ere méthode :

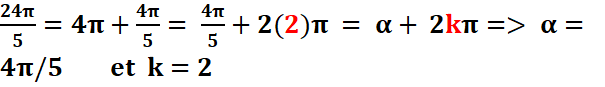
2eme méthode :α=24π/5-2kπ

α ∈] − π, π] < =>− π<α≤π

< =>− π< 24π/5 - 2kπ≤π

< =>− π-24π/5< - 2kπ≤π-24π/5

< =>− 1-24/5< -2k≤1-24/5

< =>19/10< k<29/10

< =>1,9<k<2,9

k=2 => α=24π/5 -4π=4π/5 ϵ ] − π, π]

TRIGONOMETRIE

cosinus, sinus et tangente d’un angle orienté

Considérons les lignes trigonométriques de centre O.

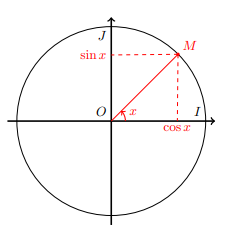
Dans un repère orthonormal direct (O,I,J), α est l’angle orienté dans le cercle unité, on a alors :

cos α = projection de l’angle sur l’axe d0,1es abscisses.

sin α = projection de l’angle sur l’axe des ordonnées.

tan α = projection de l’angle sur la droite tangente au cercle unité en (1, 0) et orientée vers le haut

Cherchons les coordonnées de M(x,y).

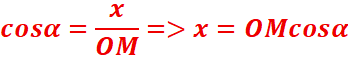
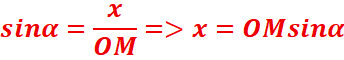
Les coordonnées du point M sont (OM cos α, OM sin α).

Ainsi l’axe des x est considéré comme l’axe des cosinus et l’axe des ordonnées comme l’axe des sinus.

Propriétés :

· Si ɑ est un angle, pour tout kϵZ

sin²ɑ +cos²ɑ = 1

-1≤sinα≤1

-1≤cosα≤1

cos(α+2kπ)=cosα

sin(α+2kπ)=sinα

· Si ɑ est un angle, pour tout kϵZ

tanα=sinα/cosα avec α≠π/2 +kπ

1/cos²α =1+tan²α

tan(α+kπ)=tanα

Ligne trigonométrique des angles remarquables

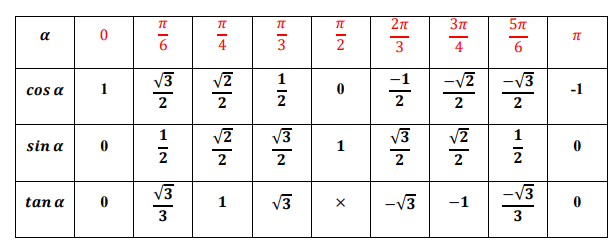
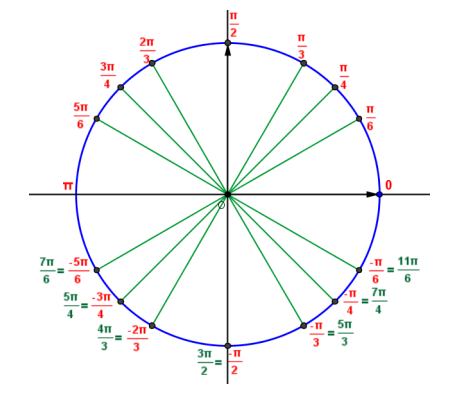
Ligne trigonométrique d’angles associées

Relations avec des angles opposées

Relation avec l’angle supplémentaire et l’opposé du supplémentaire

Exemple :

A=cos(x+5π)+cos(π-x)+sin(π/2+x)=cos(x+π) - cosx +cosx= -cosx

B= cos(x+7π)+sin(x-π/2)+cos(x-π) +cos(x+π)=cos(x+π)-sin(π/2-x)+cos(π-x) +cos(x+π)

=-cosx -cosx -cosx -cosx

= -4cosx

Relation avec l’angle complémentaire et l’opposé du complémentaire

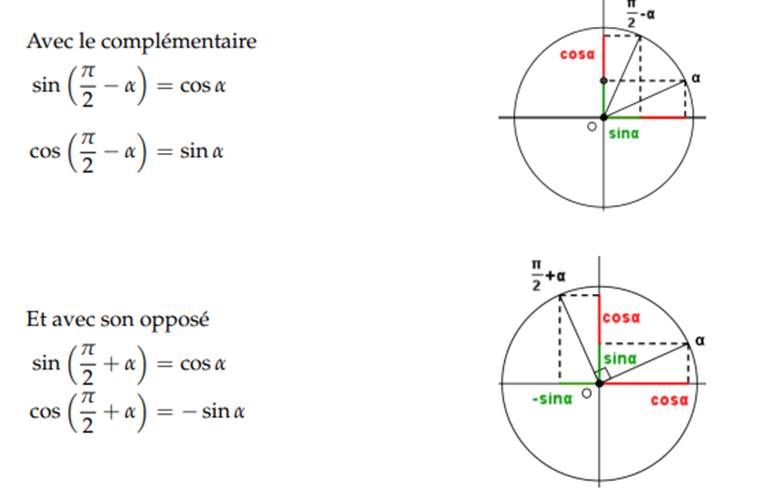
Formules trigonométriques

Formules d’addition

Etant donnes deux réels α et β

cos(α+β)=cosαcosβ-sinαsinβ

cos(α-β)=cosαcosβ+sinαsinβ

sin(α+β)=sinαcosβ+cosαsinβ

sin(α-β)=sinαcosβ-cosαsinβ

Exemple : Sachant que 7π/12=π/3+π/4, calculer cos7π/12 et sin7π/12

cos7π/12 =cos(π/3+π/4)

=cos π/3 cos π/4 -sin π/3sin π/4

=1/2xѴ2/2 -Ѵ2/2xѴ2/2=Ѵ4/4-Ѵ6/4

sin7π/12= sin(π/3+π/4)

=sin π/3cos π/4+cos π/3sin π/4

=Ѵ3/2xѴ2/2+1/2xѴ2/2

=Ѵ6/4+Ѵ2/4

Formules de linéarisation

Pout tout reel α

· cos2α=cos(α+α)=cos α cos α -sin α sin α=cos² α - sin² α

cos² α –(1- cos² α)=2cos² α – 1 =>

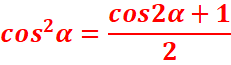
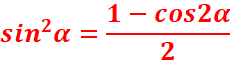
· sin2α=sin(α+α)=sinαcosα +cosαsin α => sin2α=2sinαcosα

· tan2x=sin2x/cos2x=2sinαcosα/2cos² α – 1= =>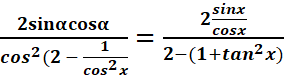

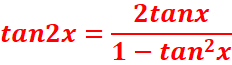
Exemple : Exprimer cos4x en fonction de cosx

cos4x=cos2(2x)

=2.2cos²2x -1

=2(2cos²x -1)² -1

=2(4cos⁴x -4cos²x +1) -1

Formules et transformation du produit en somme

cosacosb = 1/2[cos(a+b) + cos(a-b)]

sinasinb =-1/2[cos(a+b) + cos(a-b)]

sinacosb = 1/2[sin(a+b) + sin(a-b)]

cosasinb = 1/2[sin(a+b) + sin(a-b)]

Formule de transformation de la somme en produit

cosp + cosq= 2cos(p+q)/2cos(p-q)/2

cosp – cosq= -2sin(p+q)/2sin(p-q)/2

sinp + sinq= 2sin(p+q)/2cos(p-q)/2

sinp – sinq= 2cos(p+q)/2sin(p-q)/2

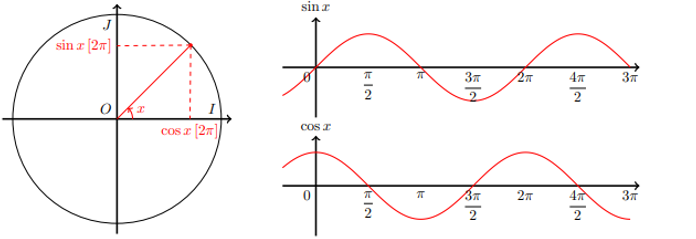
Représentation graphique de la fonction sinus et cosinus

EXERCICES

EXERCICE I : On donne le cercle trigonométrique suivant :

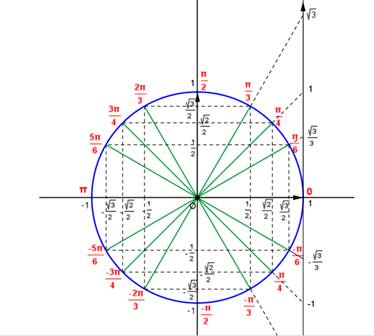
A partir du cercle trigonométrique ci-dessus :

1. Lire : cos5π/4 et cos4π/3

2. Lire : sin(π+π/6) et cos(π-π/6)

3. Lire : sin(π/2+π/6) et sin(π/2-π/6)

4. Déterminer 3 angles consécutifs de valeur principale π/3

EXERCICE II :

1.Placer, sur un cercle trigonométrique de centre O les points A, B, et C, images respectives des nombres π/4,3π/4 et -π/2 

2.Déterminer les mesures principales des angles ci-dessous :

3.Comparer les mesures principales de :

EXERCICE III :

1. Convertir en radian : 40 ° et 125 °

2. Convertir en degrés :5π/9 rad et 5π/35 rad.

3. Trouver les mesures principales des angles :21π/4 et -83π/11

EXERCICE IV :

1. Pour tout réel x, simplifier l’expression

A(x)=cos(3π-x)+cos(π/2 -x)+sin(-3 π/2-x)

2) Simplifier au maximum, pour tout réel t, l’expression (1- cost)(1 +cost)

3) Démontrez que pour tout nombre réel x,

cos⁴x-sin⁴x=cos²x-sin²x puis que cos⁴x-sin⁴x=2cos²x -1

4. Démontrer que pour tout réel x,

cos(2x)=2cos²(x)-1

Puisque vous connaissez cos π/4 et cos π/3, déterminez une valeur exacte de cos π/12 , puis de cos π/24.

EXERCICE V :

1. x réel, simplifier les expressions suivantes :

a- A(x)=cos(-x )-sin (x+π) + sin(-x) +cos(π-x)

b- B(x)=cos(π/2-x)+2cos(-x-π)-3sin(x+π/2)-sin(x+8π)

2.

a-On donne :

2. .

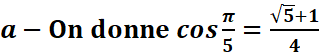
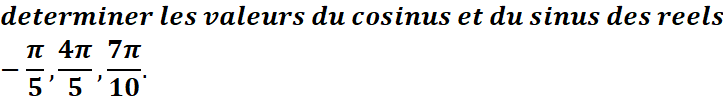
3.

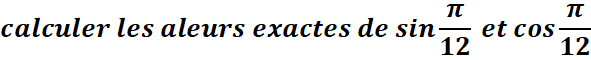
4.

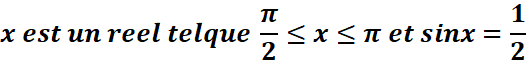
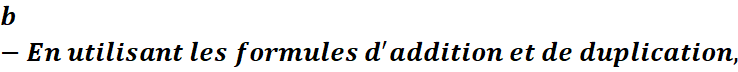
EXERCICE VI :

Soit f la fonction définie sur ℝ par :

f( x)= sin(2x).

On note (C) la représentation graphique de f dans un repère orthogonal (O ; I ; J )

1) Calculer f(0) ;f(π/6 ); f( π/12) ; f(π/2); f (π/8 );f (π);

2) Montrer que f est impaire. Que peut-on en déduire pour la courbe représentative (C) ?

3) Soit x un nombre réel.

Comparer f (x+π) et f (x). Que peut-on en déduire pour f ?

4) Démontrez que la fonction f est strictement croissante sur [-π/4, π/ 4]; puis strictement décroissante sur[ π/4, 3π/ 4]

5) Représenter graphiquement la fonction f sur l'intervalle [− 5π/4,7π/4].

CORRIGES

EXERCICE I :

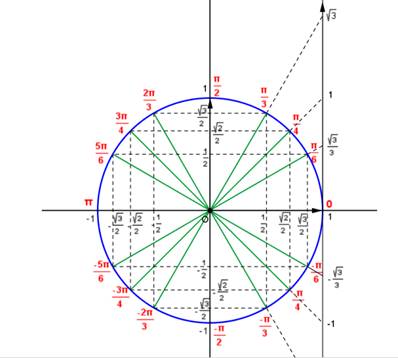
A partir du cercle trigonométrique ci-dessus :

1.cos5π/4= -Ѵ2/2 et cos4π/3=-1/2

2. sin(π+π/6)=-Ѵ3/2 et cos(π-π/6) =-Ѵ3/2

3. sin(π/2+π/6=Ѵ3/2 et sin(π/2-π/6)= Ѵ3/2

4.β= π/3+2kπ

k=1 β=π/3+2π=7π/3

k=2 β=π/3+4π=13π/3

k=3 β=π/3+6π=19π/3

EXERCICE II :

1.Placer, sur un cercle trigonométrique de centre O les points A, B et C, images respectives des nombres π/4, 3π/4 et -π/2 .

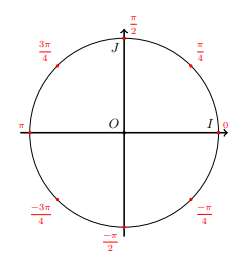
2.

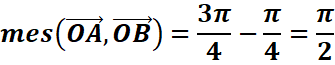
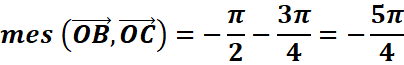
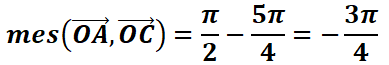
3.Comparaison

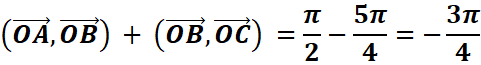
EXERCICE III :

1.

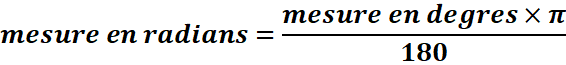
40 ° : 40xπ/180=2π/9 rad

125 ° :125xπ/180=25π/56 rad

2.

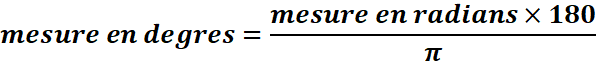
5π/9 : 5π/9x180/π=100°

5π/35 : 5π/35x180/π=25,71°

3. mesures principales des angles 21π/4 et

·

·

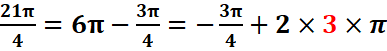
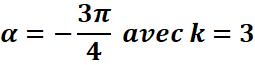
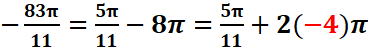
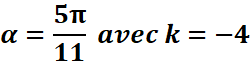
EXERCICE IV :

1. Pour tout réel x, simplifier l’expression

A(x)=cos(3π-x)+cos(π/2 -x)+sin(-3 π/2-x)

2) Simplifier au maximum, pour tout réel t, l’expression (1- cost)(1 +cost)

3) Démontrez que pour tout nombre réel x,

cos⁴x-sin⁴x=cos²x-sin²x puis que cos⁴x-sin⁴x=2cos²x -1

4. Démontrer que pour tout réel x,

cos(2x)=2cos²(x)-1

Puisque vous connaissez cos π/4 et cos π/3, déterminez une valeur exacte de cos π/12 , puis de cos π/24.

EXERCICE IV :

1 Pour tout réel x,

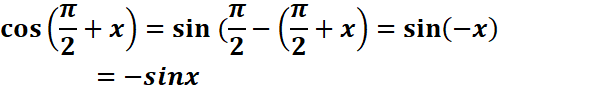
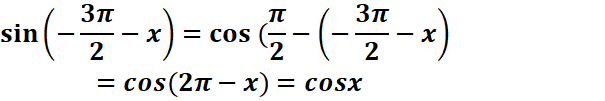
A(x)= -cosx – sinx +cosx= -sinx

2) I’expression (1- cost)(1 +cost)

=1-cosx+cos-cos²x-=(sinx)².

3) Pour tout nombre réel x,

cos⁴x-sin⁴x=(cos²x-xin²x) (cos²x+xin²x)= cos²x-sin²x

cos⁴x-sin⁴x= cos²x-xin²x= cos²x-(1-cos²x) =2 cos²x-1

4. Pour tout réel x,

cos(2x)=cos(x+x)=cosxcosx-sinxsinx=cos²x-sin²x

=cos²x-(1-cos²x)=2cos²x-1

cos(π/12)=cos(π/3 - π/4)=cosπ/3cosπ/4 + sinπ/3sinπ/4=1/2xѴ2/2 +Ѵ3/2xѴ2/2=(Ѵ2+Ѵ6)/4.

EXERCICE V:

a- A(x)=cos(-x )-sin (x+π) + sin(-x) +cos(π-x)

=cosx+sinx-sinx-cosx

=0

b-B(x)=cos(π/2-x)+2cos(-x-π)-3sin(x+π/2)-sin(x+8π)

=sinx+2cos-(x+π)-3cosx-sin(x+π)

= sinx-2cosx-3cosx-sinx

=-5cosx

2.

a-on sait que :

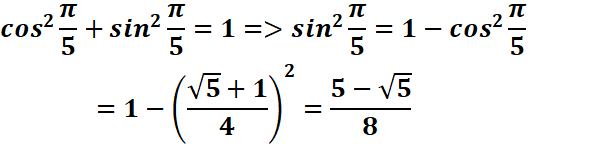
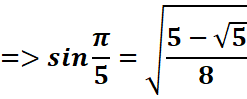
b-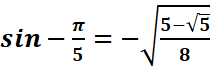

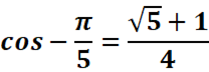
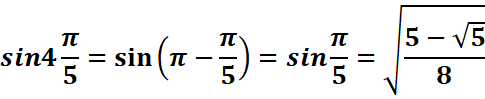
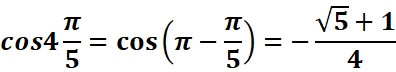
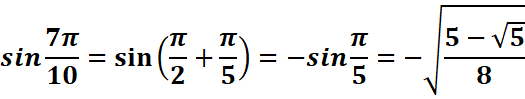
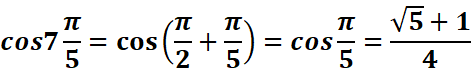
3.

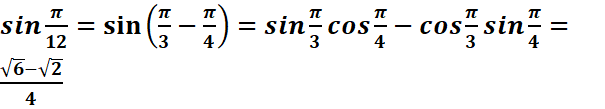
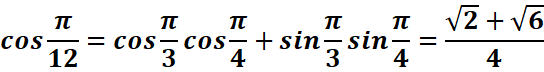
4.

( °

(

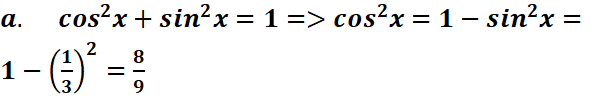
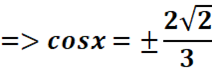
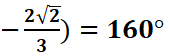
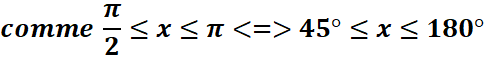
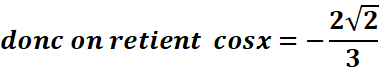
b.

EXERCICE VI:

1.On calcule f(0)=sin2(0)=0,f(π/6)=sin(2xπ/6)=Ѵ3/2, f(π/12)=sin(2xπ/12)=1/2

f(π/2)=sin(2xπ/2)=-1, f(π/8)=sin(2xπ/8)=Ѵ2/2, f(π)=sin(2xπ)=0.

2.IR est symétrique par rapport à O, et pour tout xϵIR, f(-x)=sin(2(-x))=sin(-2x)=-sin(2x)=-f(x), ce qui prouve que f est impaire. Sa courbe est donc symétrique par rapport a l’origine O du repère (O,I,J).

3.Pour tout réel x , on calcule f(x+π)=sin(2(x+π))=sin(2x)=f(x).f est une fonction périodique de période π,il suffit de l’étudier sur un intervalle d’amplitude π, par exemple [-π/4,3π/4]

4.Pour tout reel a et b de l’intervalle [-π/4,3π/4] avec -π/4≤a<b≤π/4, on a -π/2≤2a<2b≤π/2, et puisque la fonction sinus est strictement croissante sur

[-π/2, π/2], on aboutira à sin(-π/2) ≤sin2a>sin2b≥sin(3π/2), c.-à-d. -1≥f(a)<f(b)≤1. La fonction est strictement croissante sur [-π/4, π/4]

Pour tout reel a et b de l’intervalle [-π/4,3π/4] avec π/4≤a<b≤3π/4, on a π/2≤2a<2b≤3π/2, et puisque la fonction sinus est strictement décroissante sur [π/2,3π/2], on aboutira à sin(π/2) ≥sin2a>sin2b≥sin(3π/2), c.-à-d. 1≥f(a)>f(b)≥-1. La fonction est strictement décroissante sur [π/4,3π/4].

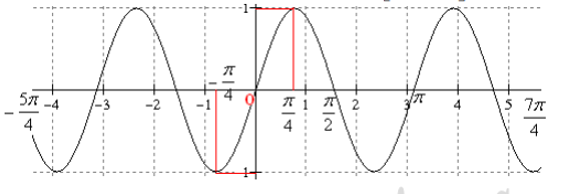
5.Representation graphique de la fonction sur l’intervalle [-5π/4,7π/4]

Avez-vous un exercice à proposer ? Cliquez-ici

Merci de votre visite
Laissez un commentaire