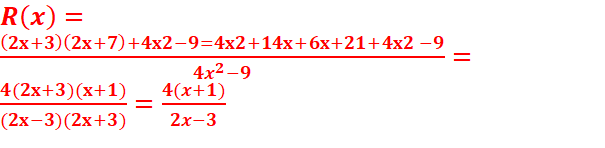CALCUL LITTERAL
MONOMES-POLYNOMES
Définitions
Ø
Un
monôme de la variable x est une expression littérale de la forme axn, où a ϵ
IR et n ϵ IN.
·
a représente le coefficient numérique ;
·
n
représente le degré du monôme,
·
x
représente la variable,
Exemples :
·
3x2
est un monôme de coefficient 3, de variable x et de degré 2.
·
5x3 est
un monôme de coefficient 5, de variable x et de degré 4.
·
-9y5
est un monôme de coefficient -9, de variable y et de degré 5.
Remarques :
·
3
est un monôme de coefficient 3, de variable x et de degré 0.
·
0
est un monôme de coefficient 0, de variable x et de degré 0.
Ø
Un polynôme
est une somme algébrique de plusieurs monômes de même variable. La variable
peut être n’importe quelle lettre de l’alphabet.
Le degré d’un polynôme est celui
de son monôme de plus haut degré.
Exemple : 2x2+5x5-7x3
est un polynôme de variable x et de degré 5.
Propriétés
1-n,
p ϵ IN axn=bxn ,
alors a=b et n=p
2-(axn)(bxp)=abxn+p
Exemple
: (3x2)(5x3)=15x5; (2x5)2=4x10
OPERATIONS SUR LES EXPRESSIONS LITTERALES
Addition
La somme de deux polynômes est un polynôme,
pour l’obtenir, on regroupe les monômes de même degré et on additionne
leurs coefficients.
Exemple :
P(x)=7x2+4x5+x+1
Q(x)=8x5-3x2+5
(P+Q)(x)= (7x2+4x5+x+1)+(8x5-3x2+5)=(
7x2-3x2) +(4x5+8x5)+(x)+(1+5) // on regroupe les monômes de même degré.
=12x5+4x2+x+6 // on
additionne leurs coefficients
Remarque :
P-Q
est aussi un polynôme
Réduire une expression littérale, c’est l’écrire avec
moins de termes. Pour cela, on regroupe les termes semblables afin d’effectuer
les opérations appropriées visant à réduire les différentes expressions.
Ordonner un polynôme revient à le ranger du monôme le
plus haut degré à celui du plus petit degré (suivant les puissances
décroissantes) ou alors du monôme au plus petit degré à celui au plus haut
degré (suivant les puissances croissantes).
Exemple :
P(x)=3x2+8x6-3x5+4x8+5
Q(x)=3x4+12x2-13x5+14x6-8
P(x)+
Q(x)=(3x2+8x6-3x5+4x8+5) +( 3x4+12x2-13x5+14x6-8)
=(3x2+12x2)
+( 8x6+14x6) +(-3x5-13x5) +(4x8)
+5-8
=15x2+22x6-16x5+4x8-3
Suivant
les puissances décroissantes, on a :
4x8+22x6-16x5+15x2-3 //les degrés
diminuent de 8 à 0 (-3=-3x0)
Suivant
les puissances croissantes, on a :
-3+15x2-16x5+22x6+4x8 //les
degrés augmentent de 0 à 8 (-3=-3x0)
Multiplication
Le produit de deux polynômes est un polynôme.
Développer un polynôme ou une expression, c’est l’écrire
sous la forme d’une somme algébrique d’autres expressions plus simples
(monômes).
Exemple :
P(x)=2x2
+x
Q(x)=x+1
P(x)xQ(x)=(2x2 +x)( x+1)=2x2.x+2x2.1+x.x+x.1 // on développe le
produit ( 2x2 +x)( x+1)=
=2x3+2x2+x2+x
=2x3+3x2+x //on
obtient une somme des monômes simples
Pour développer une
expression littérale, on peut utiliser :
Ø
La
propriété de distributivité de la multiplication sur l’addition et la
soustraction
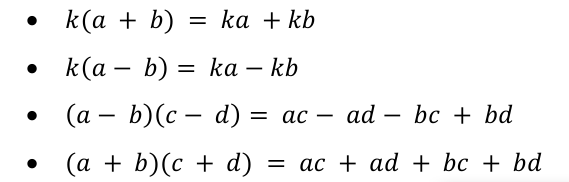
Remarque 1:
Quand on a un (+) devant la parenthèse, on
supprime les parenthèses sans rien faire d’autre. Quand on a un (-) devant la
parenthèse, on supprime les parenthèses mais en changeant tous les signes des
monômes qui se trouvent à l’intérieur des parenthèses en leur opposé.
Remarque
2 :
Dans un développement
d’une expression littérale, l’ordre de priorité est le suivant :
·
L’élévation
à une puissance ;
·
Les
opérations entre parenthèses ;
·
La
multiplication ou la division ;
·
L’addition
ou la soustraction.
Factorisation
Factoriser une expression, c’est l’écrire sous
la forme d’un produit de facteurs. C’est l’opération inverse du développement.
Méthodes de factorisation
Ø Utilisation des facteurs communs
Il s’agit d’utiliser un terme commun aux
éléments d’une somme
Exemple :
P(x)=(x+1)(x-2) -2x-2
=(x+1)(x-2) -2(x+1) // on remarque que
(x+1) est présent dans les deux termes de l’expression
=(x+1)[(x-2)-2] //on met le
terme commun en facteur
=(x+1)(x-4)
Ø Utilisation des identités remarquables.
Il s’agit de de retrouver les identités
suivantes dans l’expression des polynômes
. 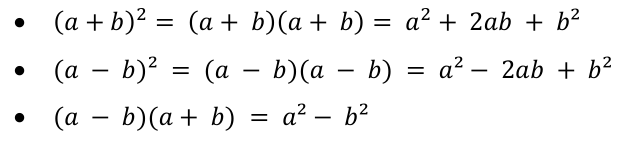
Exemples : Factoriser les
expressions suivantes :
·
P(x)=16x2-8x+1
En posant
a=4x
b=1
On
a l’identité remarquable a2-2ab +b2=(a-b)2
P(x)=16x2-8x+1=(4x)2-2(4x).1+(1)2=(4x-1)2
·
Q(x)=x2
+4x +4
En posant
a=x
b=2
On
a l’identité remarquable a2+2ab +b2=(a+b)2
Q(x)=x2 +4x +4=(x)2+2(x).2
+(2)2=(x-2)2
·
T(x)=x2-9
En posant
a=x
b=3
On
a l’identité remarquable a2-b2=(a+b)(a-b)
T(x)=(x+3)(x-3)
Ø Utilisation du début de carré
Dans l’ecriture du polynôme a factoriser, on
identifie le début du développement d’un carré c.-à-d. d’une identité
remarquable.
a2+2ab est le début de
développement de (a+b)2 puisque (a+b)2=a2+2ab+b2 => a2+2ab=(a+b)2-b2
Exemples:
·
P(x)=4x2+4x-12
P(x)=4x2+4x-12=(2x)2 +2(2x).1
On pose : a=2x et b=1
4x2+4x est le début de développement
de (2x+1)2 //car(2x+1)2=4x2
+4x +1 =>4x2 +4x=(2x+1)2-1
4x2+4x =(2x+1)2-1
P(x)=4x2+4x-12=(2x+1)2-1
-12=(2x+1)2 -13
a2-b2=(a-b)(a+b) //car (a-b)(a+b)=a2+ab-ba
-b2
P(x)=(2x+1)2
-13=[(2x+1) -Ѵ13] [(2x+1)+ Ѵ13]
·
Q(x)=x2+3x-4
x2+3x-4=(x+3/2)2-(3/2)2-4=(x+3/2)2-(5/2)2=[x+3/2-5/2][
x+3/2+5/2]=(x-1)(x+4)
Remarque :
P(x)=ax2+bx+c=a[(x+b/2a)2-(b/2a)2
+c/a]
EXPRESSION
RATIONNELLE
Une expression
rationnelle est une fraction dont le numérateur et le dénominateur sont des
polynômes.
Exemple :
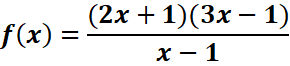
Condition d’existence d’une expression rationnelle
Comme toute fraction, l’écriture d’une
expression rationnelle n’est possible que lorsque son dénominateur est
différent de zéro : c’est la condition d’existence d’une valeur numérique de la
fraction rationnelle.
Pour
déterminer la condition d’existence d’une valeur numérique d’une fraction
rationnelle, on peut d’abord et si possible factoriser le dénominateur et
ensuite utiliser la propriété signifie que
Exemple :
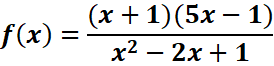
f(x)
existe si et seulement si x2-2x+1 ≠0
x2-2x+1
≠0 <= >(x-1)2≠0 donc x≠1
Simplification d’une expression rationnelle
Simplifier une expression rationnelle c’est la rendre sous la
forme la plus simple possible. Pour cela, On factorise le numérateur et le
dénominateur si cela est nécessaire ;
Méthode :
i.
On détermine la condition d’existence ;
ii.
On
élimine les facteurs communs qui apparaissent au numérateur et au dénominateur
;
iii.
Ecrire l’expression simplifiée précédée de la
condition d’existence.
Exemple :
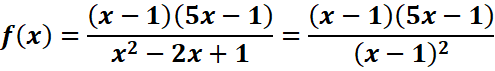
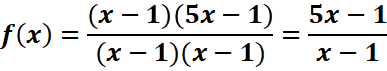
EXERCICES
EXERCICE
I :
1.Déterminer
le coefficient et le degré des monômes ci-après :20x ;36x2
; x3 ;-38x4
2.Calculer (3x)(2x2) ;(4x2)(3x)(12x5) ;(2x6)3.
3.
Calculer : (3x)+(-2x2) ; (3x)+(2x2) –(3x+12x2) ;(x+1)-(5x+4x2)(x-1)
EXERCICE
II : développer, réduire et ordonner suivant les puissances
décroissantes de x les expressions suivantes :
1.(x+1)(2x2 -x)
2.(x-1)2-(x-1)(x2+2)
3. (x2+x)(x-3)+x3(x2-1)
4. x3(x2-1)+x4 -(x-1)(x2+2)
EXERCICE
III : Factoriser les expressions suivantes :
1.(x-1)(x+1)- (x-1)(2x+1)-(x-1)(3x+2)
2.x2-4
+(x-2)(x+4)-2(x-2)
3.(x3+5x2)+(x+5)(-x2-2) +x2+10x+25
4.(x+2)2
+(-x-2)(3x-2)-(2x+1)(x+2)
EXERCICE
IV : Factoriser les expressions suivantes :
1.x2-6x+9
2.16x2-8x+1
3.x2+2x-3
4.x2-x-6
5. 4x2
+6x-4
EXERCICE V :

CORRIGES
EXERCICE I :
1.Déterminer le coefficient et le degré des monômes ci-après :
|
|
20x |
5 |
36x2 |
x3 |
-38x4 |
|
Coefficient |
20 |
5 |
36 |
1 |
-38 |
|
Degré |
1 |
0 |
2 |
3 |
4 |
2.Calculer ;
(3x)(2x2) =6x3
(4x2)(3x)(12x5)=144x2+1+5=144x8
(2x6)3. =23x6x3=8x18
3. Calculer :
(3x)+(-2x2) =3x-2x2
(3x)+(2x2) –(3x+12x2) =3x+2x2
–3x-12x2=-10x2
(x+1)-(5x+4x2)(x-1)=x+1 –(5x2+4x3-5x-4x2)=
1 –x2-4x3+6x
EXERCICE II : développer, réduire
et ordonner suivant les puissances décroissantes de x les expressions
suivantes :
1.(x+1)(2x2 -x)=2x3-x2+2x2-x=2x3+x2-x
2.(x-1)2-(x-1)(x2+2)=(x2-2x+1)
-[x3+2x-x2-2]= x2-2x+1 -x3-2x+x2+2=2x2-4x+3-x3=-x3+2x2-4x+3
3. (x2+x)(x-3)+x3(x2-1)=x3-3x2+x2-3x
+x5-x3=x5-2x2-3x
4. x3(x2-1)+x4
-(x-1)(x2+2)=x5-x3+x4-[x3+2x-x2-2]=x5+x4-2x3+x2-
2x+2
EXERCICE III : Factoriser les expressions
suivantes :
1.(x-1)(x+1)- (x-1)(2x+1)-(x-1)(3x+2) //on identifie le facteur commun (x+1)
=(x-1)[(x+1)-(2x+1)-(3x+2)] //on le met en facteur
=(x-1)[x+1-2x-1-3x-2] //on chasse d’abord les parenthèses
=(x-1)[-4x-2] //puis les crochets
=2(x-1)(-2x-1)
2.x2-4 +(x-2)(x+4)-2(x-2) //on remarque que x2-4=(x-2)(x+2)
=(x-2)(x+2)+ (x-2)(x+4)-2(x-2) //le facteur commun apparait.
=(x-2)[(x+2)+ (x+4)-2]
=(x-2)[x+2+ x+4-2]
=(x-2)[2x+4]
=2(x-2)[x+2]
3.(x3+5x2)+(x+5)(-x2-2)
+x2+10x+25//on
remarque que x2+10x+25=(x+5)(x+5)
=x2(x+5)+ (x+5)( -x2-2)+(x+5)(x+5)
=(x+5)[x2+ (-x2-2)+(x+5)]
=(x+5)[x2+ -x2-2+x+5]
=(x+5)[x+3]
4.(x+2)2 +(-x-2)(3x-2)-(2x+1)x+2)
=(x+2)(x+2)-(x+2)(3x-2)- (2x+1)(x+2)
=(x+2)[(x+2)-(3x-2)- (2x+1)]
=(x+2)[x+2-3x+2- 2x-1]
=(x+2)[-4x+3]
EXERCICE IV : Factoriser les expressions
suivantes :
1.x2-6x+9= x2-2(3x)+(3)2=(x-3)2 //identité remarquable
2.16x2-8x+1=(4x)2 -2(4x)+(1)2=(4x-1)2//identité remarquable
3.x2+2x-3=(x+1)2-(1)2-3=(x+1)2-22=[(x+1)-2][ (x+1)+2]=(x-1)(x+3) // x2+2x est le début de (x+1)2
4.x2-x-6=(x-1/2)2-(1/2)2-6=(x-1/2)2-1/4-6=(x-1/2)2-(5/2)2=[(x-1/2)-(5/2)][ (x-1/2)+(5/2)]=(x-3)(x+2) // x2+x est le début de (x+1/2)2
5. 4x2 +6x-4=(2x +3/2)2-(3/2)2-4=(2x
+3/2)2 -9/4-4=(2x +3/2)2-25/4=[(2x +3/2)-5/2][ (2x
+3/2)+5/2]=(2x-1)(2x+4) // 4x2+6x est le
début de (2x+3/2)2
EXERCICE IV :
1. P(x)=(2x+3)(2x+7) +4x2-9=4x2+14x+6x+21+4x2
-9=+12+20x+8x2
2. Degre = 2
3. Q(x)=4x2-9=(2x-3)(2x+3)
P(x)=(2x+3)(2x+7) +4x2-9=
P(x)=(2x+3)(2x+7) +(2x-3)(2x+3) =(2x+3)[(2x+7)
+(2x-3)]=(2x+3)[(4x+4)]=4(2x+3)(x+1)
4. R(x)=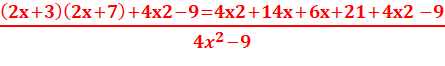
5.
R(x) existe si et seulement si 4x2-9≠0
< =>(2x-3)(2x+3)≠0
< =>(2x-3)≠ et (2x+3)≠0= x≠-3/2 et x≠3/2
6.