STATISTIQUES

VOCABULAIRE STATISTIQUE

On a demandé à 20 élèves de la 3eme d’indiquer leur sport préféré.

Reponses: F(football); F; A (athlétisme); F; Bo (Boxe); Bo; F; A; H(Handball); Ba (Basketball); F; Bo; Ba; F; A; Ba; Ba; F; F; F.

·         L’ensemble des élèves interrogés est la population étudiée.

·         La liste des réponses relevées est la série statistique.

·         Le caractère étudié est le sport préféré.

·         F, A, Bo, H, Ba sont les modalités de cette série statistique.

·         L’effectif d’une modalité est le nombre de fois ou cette modalité a été relevée dans la série statistiques.

·         L’effectif total est la somme des effectifs de toutes les modalités.

Pour faciliter la lecture, on présente souvent les effectifs sous forme de tableau :

 

Modalités

F

A

Ba

H

Bo

Total

Effectifs

9

3

4

1

3

20

 

DEFINITIONS

Série statistique

On appelle série statistique une suite de valeurs que prend un caractère au sein d’une population.

Lorsqu’une série statistique est regroupée en intervalles, on dit qu’elle est regroupée en classes ; et chacun de ces intervalles est appelé une classe.

L’effectif d’une classe est le nombre d’individus dont les modalités appartiennent à cette classe.

Exemple : On a regroupé dans le tableau ci-dessous le nombre d’avocatiers d’une pépinière en fonction de leur taille en cm. La série statistique obtenue est regroupée en classes comme suit :

30 avocatiers ont une taille comprise entre 0 et 5 cm

12 avocatiers ont une taille comprise entre 10 et 15 cm

…

Amplitude

 · L’amplitude d’une classe [a,b[ est le nombre b-a

Pour la classe [ 10,15[,

L’amplitude est 15-10=5

Centre

· Le centre est le nombre (a+b) /2

Exemple : le centre la classe [ 10,15[ est (10+15) /2=12,5

Classe modale

La classe modale est la classe ayant le plus grand effectif. Le mode est le centre de la classe modale.

Exemple Dans l’exemple ci-dessus, la classe modale est la classe [5 ; 10[.

Fréquence

 La fréquence en pourcentage d’une classe est donnée par la formule :

 Fréquence de la classe [ a,b[ =

Exemple : la fréquence de la classe [5,10 [   est :

 Remarque : la somme de toutes les fréquences en pourcentage est toujours égale à 100.

Moyenne :

            La moyenne d’une série statistique regroupée en classes est donnée par la formule :

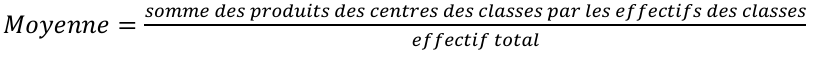
Exemple :

 

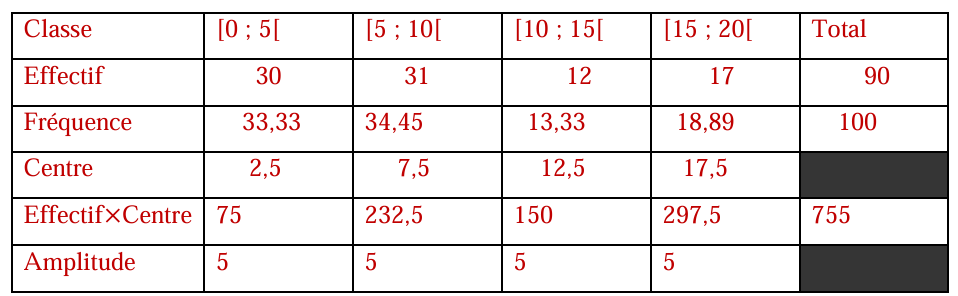
 Moyenne =755/90=8,38

LES DIAGRAMMES

 Le diagramme a bandes.

 Il est construit de telle manière qu’un grand tuyau rectangulaire est divisé en bandes de longueurs proportionnelles à l’effectif ou la fréquence de la modalité représentée.

 Exemple :

On a interrogé 1253 individus de différentes classes d’âge sur le nombre de fois qu’ils utilisent internet par mois. Les réponses sont consignes dans le tableau ci-dessous :

age

[10,20[

[20,30[

[30,40[

[40,50[

[50,60[

[60,70[

total

Nombre de fois

551

276

288

100

25

13

1253

 

La totalité des fréquences est représentée par une bande rectangulaire de longueur 12 cm. La valeur de la classe [10,20[  est représentée par une bande (verte) de longueur x 12 = 5,28 cm. En effet, la valeur de la classe [10,20[  correspond à 44 % du tout, soit 44 % de 12. On fait de même pour calculer la longueur des autres bandes.

 

[10,20[

[20,30[

[30,40[

[40,50[

[50,60[

[60,70[

 

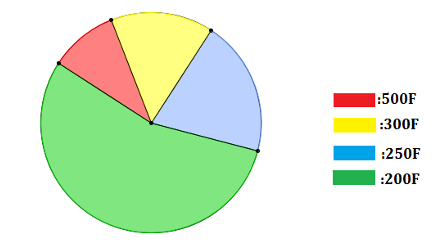
Le diagramme circulaire ou par secteur.

Lors de la construction du diagramme circulaire, chaque secteur du cercle représente une modalité du caractère ou variable. L’angle au centre est déterminé par la formule:

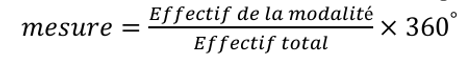
ou encore par la formule :

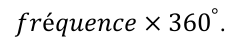
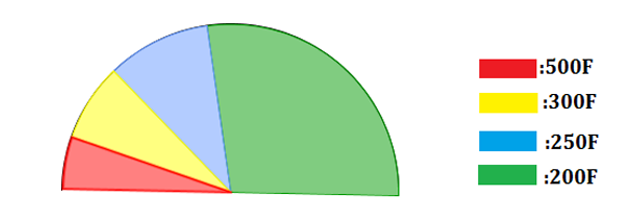
 Exemple :  Dans une librairie, on compte le nombre de cahiers de 200,250,300 e 500 fcfa. On trouve 363 cahiers de 200, 132 cahiers de 250,99 cahiers de 300 et 66 cahiers 500.Les résultats sont enregistrés dans le tableau ci-dessous :

Le diagramme par secteur est :

 

Le diagramme semi-circulaire

 

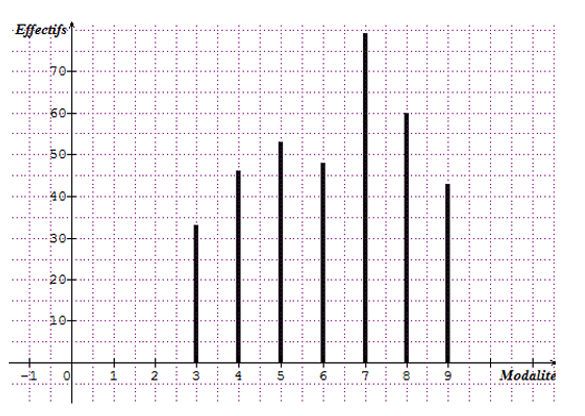
Le diagramme en bâtons.

Un diagramme en bâtons est une représentation graphique des données statistiques a l’aide des segments. Les valeurs du caractère étudié sur l’axe horizontal, les effectifs sur l’axe vertical. A chaque valeur correspond un bâton. Les hauteurs des bâtons sont proportionnelles aux effectifs représentés. Le diagramme en bâtons est adapté pour représenter des caractères statistiques, dont les valeurs sont qualitatives ou quantitatives.il est très utilise pour représenter les effectifs et les fréquences.

Exemple :

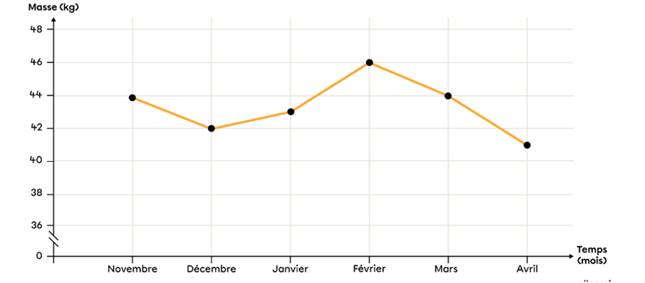
 Le diagramme a lignes brisées.

Les diagrammes à lignes brisées qu'on appelle aussi diagrammes linéaires et aussi diagrammes à courbes sont utilisés pour illustrer la progression ou la régression de données enregistrées dans le temps.

 Les caractéristiques du diagramme à ligne brisée sont les suivantes.

Exemple : Représentons la masse d’une personne, relevée entre Novembre et Avril 2025

 

Mois

Nov

Dec

Janv

Fev

Mars

Avril

Masse(kg)

44

42

43

46

44

41

 

 

 

 

EXERCICES

EXERCICE I :

Les notes sur 20 obtenus lors d’un devoir de maths dans une classe de seconde sont :10 ; 8 ; 11 ; 9 ; 12 ; 10 ; 8 ;10 ; 7 ; 9 ; 10 ;11 ;12 ;10 ; 8 ;9 ;10 ; 9 ;10 ; 11.

1.Identifier la population, le caractère étudiée et l’effectif de cette série statistique.

2. Compléter le tableau ci-dessous :

 Modalité(xi)

7

8

9

 

 

12

Total

Effectif(ni)

 

 

4

7

3

 

 

Fréquence

 

 

 

 

 

 

 

 

 3.Quelle est la moyenne de cette série statistique ?

EXERCICE II :

Dans un club de football, les dirigeants ont relevé l’âge des joueurs :

 

a. Calcule la moyenne pondérée des âges des joueurs.

 b. Recopie et complète le tableau suivant :

c. Calcule la moyenne par classe des âges.

d. Comment expliques-tu la différence entre les deux calculs de moyenne ?

 

EXERCICE III :

On interroge les élèves d’une classe sur leur taille en cm. Voici les résultats de l’enquête : 174 – 160 – 161 – 166 – 177 – 172 – 157 – 175 – 162 – 169 – 160 – 165 – 170 – 152 – 168 – 156 – 163 – 167 – 169 – 158 – 164 – 151 – 162 – 166 – 156 – 165 – 179

 1) Calculer l’étendue de la série de tailles.

 2) Regrouper les effectifs de cette série de tailles par classes de longueur 5 cm et présenter les résultats dans un histogramme.

 3) Calculer les fréquences de chaque classe en % au centième près.

4)

 a) Calculer la moyenne de la série après avoir centré les classes.

 b) Comparer le résultat précédent avec la moyenne exacte.

 

CORRIGES

EXERCICE I :

1.notes de maths.

2. Compléter le tableau ci-dessous :

Modalité(xi)

7

8

9

10

11

12

Total

Effectif(ni)

1

3

4

7

3

2

20

Fréquence

0.05

0,15

0.20

0,35

0,15

0,10

1

 

 3.

 

EXERCICE II :

 

a.

 b. tableau :

 

Age

[5,8]

]8,12]

]12,15]

]15,18]

Total

Nombre de joueurs

4

4

3

3

14

ci

6,5

10

13,5

16,5

 

nici

26

40

40,5

49,5

156

 

 

 

 

 

 

 

c. 

d.

 

EXERCICE III :

1) Étendue = Plus grande valeur – Plus petite valeur Étendue des tailles = 179 – 151 = 28 cm

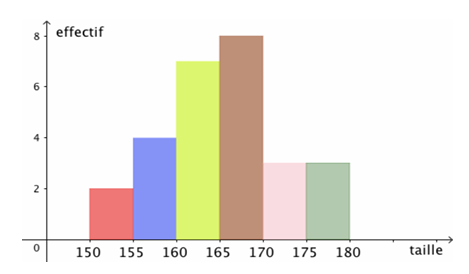
2) Regroupement de la série de tailles par classes de longueur 5 cm :

Taille

[150,155[

[155,160[

[160,165[

[165,170[

[170,175[

[175,180[

Effectifs

2

4

7

8

3

3

 

 

3) Calculer les fréquences de chaque classe en % arrondies à l’unité

Taille

[150,155[

[155,160[

[160,165[

[165,170[

[170,175[

[175,180[

total

Effectifs

2

4

7

8

3

3

27

fréquence

0,07

0,15

0,26

0,30

0,11

0,11

1

.

4) Moyennes :

a) Calcul de la moyenne en centrant les classes :

Il s’agit d’un calcul de moyenne pondéré : (152,5 x 2 + 157,5 x 4 + 162,5 x 7 + 167,5 x 8 + 172,5 x 3 + 177,5 x 3) : 27 = 4462,5 : 27 = 165,3 cm 

b) Calcul de la moyenne exacte : (174 + 160 + 161 + 166 + 177 + 172 + 157+ 175 + 162 + 169 + 160 + 165 + 170 + 152 + 168 + 156 + 163 + 167+ 169 + 158 + 164 + 151 + 162 + 166+ 156 + 165 + 179) : 27 = 4444 : 27 = 164,6 cm

 La méthode de calcul de moyenne en centrant les classes est assez fiable : 7 mm d’erreur.