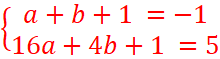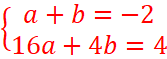REPRÉSENTATION GRAPHIQUE D’UNE FONCTION
BRANCHES INFINIES D’UNE REPRESENTATION GRAPHIQUE
Asymptote verticale
Lorsque la
fonction f(x) tend vers l’infini quand x tend vers a, la droite d’équation x=a
est asymptote verticale.

Exemple :
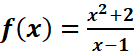 ,
,
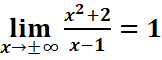 => la droite y=1 est asymptote verticale.
=> la droite y=1 est asymptote verticale.
Asymptote horizontale
Lorsque la fonction f(x) tend vers
un nombre b quand x tend vers l’infini, la droite d’équation y=b est asymptote
horizontale.
![]()
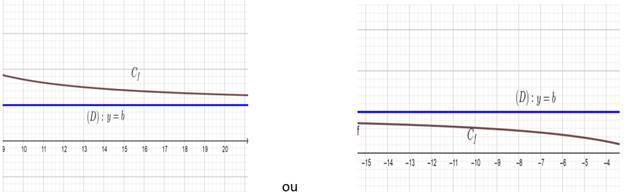
Exemple :
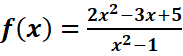 ,
,
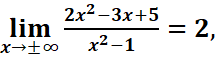 => la droite y=2 est asymptote horizontale.
=> la droite y=2 est asymptote horizontale.
Asymptote oblique
La droite y=ax + b
est une asymptote oblique à la courbe en ![]()
![]() =0
=0

Branches paraboliques
Lorsque la fonction f(x) tend vers l’infini quand. X tend
vers l’infini, la courbe Cf représentative de la fonction admet une branche parabolique.
Si ![]() =+
=+![]() alors la courbe admet une branche parabolique.
alors la courbe admet une branche parabolique.
· 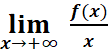 =0 =>
la courbe admet une branche parabolique de direction (O, I).
=0 =>
la courbe admet une branche parabolique de direction (O, I).
· 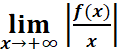 =
=![]() => la courbe admet une branche parabolique
de direction (O, J).
=> la courbe admet une branche parabolique
de direction (O, J).
Position relative de la courbe par
rapport à son asymptote.
La position relative entre deux courbes Cf et
Cg est donnée par le signe de la différence f(x)-g(x).
·
Si
f(x)-g(x)>0 sur l’ensemble I, Cf est au-dessus (strictement) de Cg sur cet
ensemble de points.
·
Si
f(x)-g(x)<0 sur l’ensemble I, Cf est au-dessous (strictement) de Cg sur cet
ensemble de points.
·
Si
f(x)-g(x)=0 sur l’ensemble I, Cf coupe Cg sur cet ensemble de points.
ETAPES DE L’ETUDE
D’UNE FONCTION POLYNOME OU RATIONNELLE
a)
déterminer le domaine de définition
b) déterminer les
limites aux bornes du domaine de définition ;
c) déterminer ou
justifier l’existence des asymptotes ;
d) déterminer le sens
de variation et dresser le tableau de variation ;
e) déterminer ou
justifier l’existence des éléments de symétries ;
f) déterminer
l’équation de certaines tangentes :
g) déterminer les
points de rencontre avec les axes et dresser une table des valeurs
h) tracer soigneusement
la courbe
EXERCICES
EXERCICE
I :
A-Soit la fonction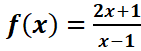 .Cochez la
bonne réponse.
.Cochez la
bonne réponse.
1-Le domaine de définition de f
est :
a) R\{0} b) R\{1} c) R\{2} d) R\{-1}
2-L’image par f de 0 est :
a) -2 b) 2 c) 1 d) -1
3-La limite de f(x) lorsque x tend
vers -1 est :
a) -1/2 b) 1/2 c)3/2 d) -3/2
4-Le nombre dérivé au point x0=2
est :
a) -3 b) 2 c) 3 d)-2
5-L’équation de la tangente au point
x0=0 est :
a) y=0 b) y=2 c) y=-3x-1 d) y=x+2
B-Soit
la fonction f(x)=2(x2 +1)2. Cochez la bonne réponse.
1-Le domaine de
définition de f est :
a) ] - ∞ ;
+∞[ b) [+∞ ;- ∞] c) [ - ∞ ;
+∞[ d) ] +∞ ;- ∞[
2-L’image par f de 0
est :
a) 4 b) -4 c) -2 d) 2
3-La limite de f(x)
lorsque x tend vers -1 est :
a) 8 b) 4 c)-8 d) -4
4-Le nombre dérivé au
point x0=-1 est :
a) 16 b) 8 c) -16 d)-8
5-L’équation de la
tangente au point x0=0 est :
a) y=0 b) y=2 c) y=1 d) y=x+2
EXERCICE
II :
Soit f la fonction numérique définie
sur l’intervalle [ -2 ;4] par f(x)=-x2 + 2x
On note (C) sa courbe représentative dans le plan rapporté à un repère
orthogonal (O,I,J).
1-Déterminer les images de -2 et 4
2-Calculer la dérivée de f et étudier son signe sur [-2; 4]
3-Dresser le tableau de variation de f.
4-Tracer la courbe (C) de la fonction f dans le repère
(O, I, J)
5-Déduire dans le même repère la courbe (C’) de la
fonction g définie par g(x) = |f(x)|
EXERCICE III :
On donne la fonction 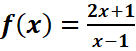 définie sur [-1 ; +∞[ et Cf sa courbe
représentative dans un repère orthonormé (O,I,J)
d’unité 2cm.
définie sur [-1 ; +∞[ et Cf sa courbe
représentative dans un repère orthonormé (O,I,J)
d’unité 2cm.
1- Calculer f(-1).
2-Calculer la dérivée de f(x).
3-Montrer qu’on peut trouver deux réels a et b tels
que 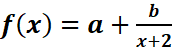 , a et b sont des coefficients réels.
, a et b sont des coefficients réels.
4- Dresser le tableau de variation de f.
5- Déterminer une équation cartésienne de la tangente
(T) à la courbe de f au point d’abscisse x0=3.
6-Montrer que la droite (D) d’équation y=2 est une
asymptote.
7- Tracer la courbe (T), (D) puis la courbe Cf.
EXERCICE IV :
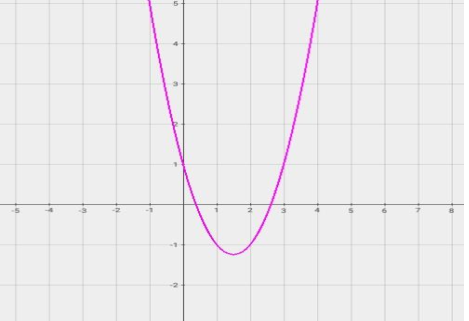
On considère la courbe (C) de la fonction f donnée
ci-contre. En s’inspirant de ce graphique, répondre aux questions
suivantes :
|
1-Déterminer l’ensemble de définition de f. 2-Déterminer les réels f (-1) et f (4). 3-Déterminer graphiquement les solutions dans
[-1 ; 4] de : a) f(x)=0 b) f(x)≤
0 c) f(x)=1 d) f(x) 4-Dresser le tableau de variation de f sur
[-1 ; 4] 5-Que représente le point S(1,5 ;-1,2) pour la courbe ( C
) ? 6-On pose f(x) = ax2 + bx + 7-Reproduire la courbe (C) et en déduire dans le
même repère, la courbe (C’) de la fonction définie dans [ -1 ; 4] par
g(x) = | f(x)| |
|
EXERCICE
V :
EXERCICE VI :
CORRIGES
EXERCICE I :
1-b
2-d
3-b
4-a
5-c
EXERCICE II :
1-Déterminer
les images de -2
et 4
f(-2)=-(-2)2+2(- 2)=-4-4=-8
f(4)=-(4)2+2(4) =-16+8=-8
2-Calcul de
la dérivée de f et étude de son signe sur [-2; 4]
f’(x)=-2x+2
f’(x)=0 <=>-2x+2=0 =>x=1
f(1)=-(1)2 +2(1)=1
Le point A(1,1) est un extrémum.
Pour tout xϵ
[-2 ; 1], f’(x) ≥0 => la courbe de f est
croissante.
Pour tout xϵ
[1 ; 4], f’(x)![]() ≤0 => la courbe de f est décroissante.
≤0 => la courbe de f est décroissante.
3- Tableau
de variation de f.
|
x |
-2
1
4 |
|
|
f’(x) |
+ |
- |
|
f(x) |
-8.
1
-8 |
|
EXERCICE III :
On donne la
fonction 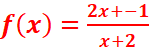 définie sur [-1 ; +∞[ et Cf sa courbe représentative dans
un repère orthonormé (O,I,J) d’unité 2cm.
définie sur [-1 ; +∞[ et Cf sa courbe représentative dans
un repère orthonormé (O,I,J) d’unité 2cm.
1- Calculer f(-1).
![]()
2-Calculer la
dérivée de f(x).
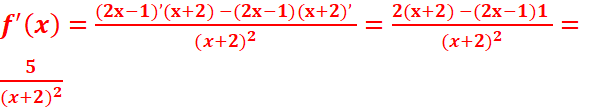
3-Montrer qu’on
peut trouver deux réels a et b tels que ![]() , a et b sont des coefficients réels.
, a et b sont des coefficients réels.
![]()
![]()
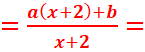
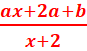 or f(x) est aussi égal à
or f(x) est aussi égal à ![]()
On obtient par
identification a=2 et 2a+b=-1. => -1-2(2)=-5
![]()
4- Dresser le
tableau de variation de f.
|
x |
-1
+∞ |
|
f’(x) |
+ |
|
f(x) |
|
5- Déterminer une
équation cartésienne de la tangente (T) à la courbe de f au point d’abscisse x0=3.
![]()
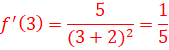
y=f’(x0)(x-x0) +f(x0). <=> 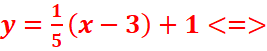
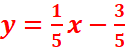 +1=
+1=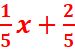
6-![]()
![]()
EXERCICE IV :
|
1-Df= [-1 ;
4] 2-Déterminer les
réels f (-1) et f(4). f(-1)=5 f(4)=5 3-Déterminer
graphiquement les solutions dans [-2 ; 4] de : a)
S= b)
S= [0,4 ; 2,6] c)
S= d) S= 4-Dresser le
tableau de variation de f sur [-1 ; 4]
5-Minimum 6- f(1)=a(1)2+b(1)+ f(4)=a(4)2+b(4)+ f(x)=x2-3x+1 |
|
|||||||||
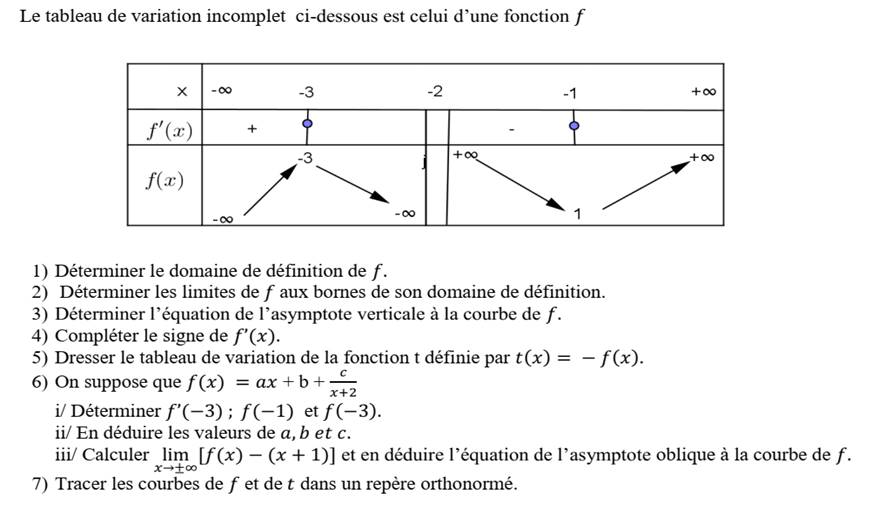
EXERCICE V :
1-
![]()
2-![]()
![]()
![]()
![]()
3) x=-2
4)
5)
La courbe de la fonction x ↣
- f(x) s’obtient de celle de f en faisant une symétrie par rapport à l’axe des
abscisses. Ses variations sont contraires à celles de f.
6)f(-3)=-3 ;f(-1)=1 et f’(-3)=0
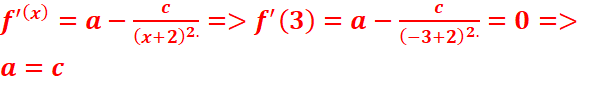
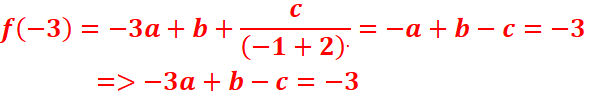
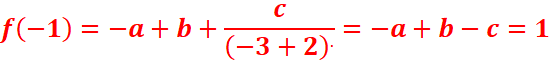
=> 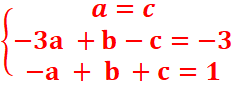
![]()
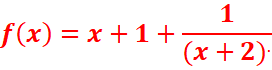
7)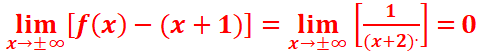
=>y=x+1 est asymptote oblique à la courbe de f.
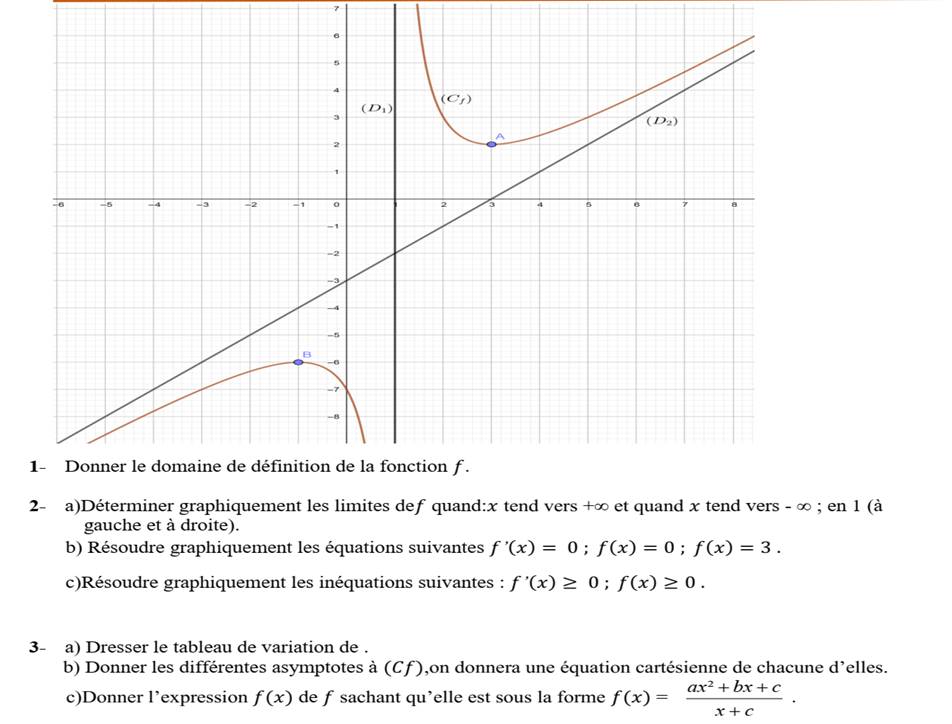
EXERCICES VI :
1- ![]() U
U![]()
2a)![]()
![]()
![]()
![]()
b) f’(x)=0 ; S={-1,3}
f(x)=0 ; S=Փ
f(x)=3 ; S={2,5}
c) f’(x)≥0;![]() S=]-∞,-1]U[3.+∞[
S=]-∞,-1]U[3.+∞[
f(x)≥0; S=]1,+∞[
3-a)
|
x |
-∞
-1
1
3 + |
||||
|
f’(x) |
+ |
- |
|
- |
+ |
|
f(x) |
|
|
|
||
b) La droite (D1) d’équation x=1 est
asymptote verticale car ![]()
La droite (D2) d’équation y=ax +b est asymptote oblique
Le point de coordonnées (3 ;0)
appartient à (D2) <=>0=3a +b
Le point de coordonnées (0 ;-3) appartient à (D2) <=>-3=a(0)
+b => b=-3 et a=1 donc y=x-3 est asymptote oblique.
c)f(x)
admet y=x-3 comme asymptote oblique donc f(x peut
s’écrire sous la forme
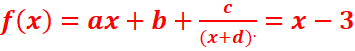 +
+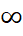
f(-1)=-6 <=>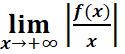 =-6 =>c=-2d+2
=-6 =>c=-2d+2
f(3)=2 <=>
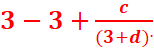 =2 =>c=2d+6
=2 =>c=2d+6
- 2d+2=2d+6 =>-4d=4
=>d=-1 par la suite c=4
Donc ![]() +
+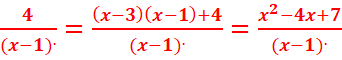
Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire