NOTIONS D’INTERVALLES

DEFINITION

               Un intervalle de IR est l’ensemble de tous les nombres réels compris entre deux valeurs a et b appelées bornes de cet intervalle. :

a et b pouvant être moins l’infini (←) ou plus l’infini (→) .

Notation : Un intervalle s’écrit avec les crochets [ ].

Exemples :[-5,0] ; [2,8]

INTERVALLES ET INEGALITES

Soient 0 et I deux réels tels que 0 < I, représentés sur la droite graduée (D).

               La partie limitée par 0 et I sur la droite graduée représente les réels compris entre 0 et I.

·        Si x est l’un de ces nombres, on peut écrire : 0 ≤ x ≤I  

Cette inégalité peut être représentée par l’intervalle fermé noté :[0,I]

·        Si x ne peut pas prendre les valeurs de 0 et de I, l’inégalité devient : 0<x<I

Cette inégalité peut être représentée par l’intervalle ouvert noté :  ]0, I [

·        Si x ne peut pas prendre la valeur de 0, mais pas la valeur de I, l’inégalité devient :   0 ≤ x <I  

Cette inégalité peut être représentée par l’intervalle semi-ouvert noté : [0, I [

·        Si x ne peut pas prendre la valeur de 0, mais celle de I, l’inégalité devient :   0 < x ≤I

Cette inégalité peut être représentée par l’intervalle semi-fermé noté : ]0, I]

Si l’une des bornes de l’intervalle n’est pas finie, on dit qu’on a un intervalle infini. 

Dans ce cas :

·   Pour l’inégalité x > 0, on a l’intervalle ]0, → [

·    Pour l’inégalité x≥0, on a l’intervalle [0, → [

·   Pour l’inégalité x < 0, on a l’intervalle ]←,0[

·    Pour l’inégalité x ≤0, on a l’intervalle ] ←,0]

INTERSECTION ET REUNION DEUX INTERVALLES

E et F sont des intervalles de R.
· L’intersection de E et F est constitué des nombres réels qui appartiennent à la fois
à E et à F. On note   E ∩ F  qui se lit E inter F.
· La réunion de E et F est constitué des nombres réels qui appartiennent à E ou à F.
On note E ⋃ F  qui se lit E union F.

On peut lire sur cette droite graduée :

Intervalle E : [-2,5]

Intervalle F :[3,→[

Intervalle E ∩ F : [3,5]

Intervalle E ⋃ F  :[-2,→[

EXERCICES

EXERCICE I:

1. Ecrire sous forme d’intervalle

a) -5 ≤ x < 1

b) 4≤x≤18

c) 3<x≤8

d)-12<x<15

2. Ecrire sous forme d’inégalité

a) x∈[-2,1]

b) x ∈ ]4,8]

c) x ∈ ]0,10[

d) x ∈ [-6,1[

EXERCICE II : On donne les intervalles I=[-2 ;5] et J=[1 ;8]

1. Représenter sur une même droite graduée :I, J et IUJ

2. Représenter sur une même droite graduée :I, J et I⋂J

3. Ecrire sous forme d’intervalle IUJ et I⋂J

EXERCICE III :

Soit une droite(D) graduée de repère (O, I).

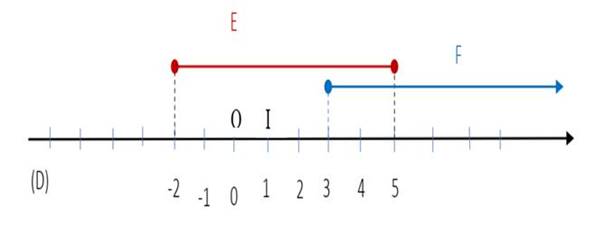
1) Donner sous forme d’intervalle l’ensemble des points en rouge (E) sur cette droite.
2) Donner sous forme d’intervalle l’ensemble des points en bleu (F) sur cette droite.
3) Peux- tu traduire par une inégalité l’ensemble des points dont l’abscisse vérifie E et F à
la fois.
4) Traduis par une inégalité l’ensemble des points dont l’abscisse vérifie E ou F.

EXERCICE IV : on donne la droite graduée suivante :

1. Donner sous forme d’intervalle I l’ensemble des points en rouge sur cette droite.

2. Donner sous forme d’intervalle J l’ensemble des points en bleu sur cette droite.

3. Donner sous forme d’intervalle IUJ et I⋂J.

EXERCICE V :

Compléter le tableau ci-dessous :

CORRIGES

EXERCICE I:

1. Ecrivons sous forme d’intervalle

a)  x∈ [-5,1[

b) x ∈ [4,18]

c) x ∈ ]3,8]

d) x ∈]-12,15[

2. Ecrivons sous forme d’inégalité

a)  -2 ≤x≤1

b)    4<x≤8

c)   0<x<10

d)-6≤x<1

EXERCICE II :.

1.     I en rouge

J en bleu

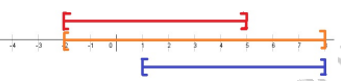
IUJ=[-2 ;8] en orange

2.

   3.  IUJ=[-2 ;8] en orange et  I⋂J=[1 ;5]  en vert

EXERCICE III:

E= [-2,5]

F= [3, → [

  3≤x≤5

-2≤x<+∞

EXERCICE IV : on donne la droite graduée suivante :

1. I =]← ;2]

2. J =]-1 ;→[

3. IUJ= ]← ;→[

I⋂J=]-1 ;2]