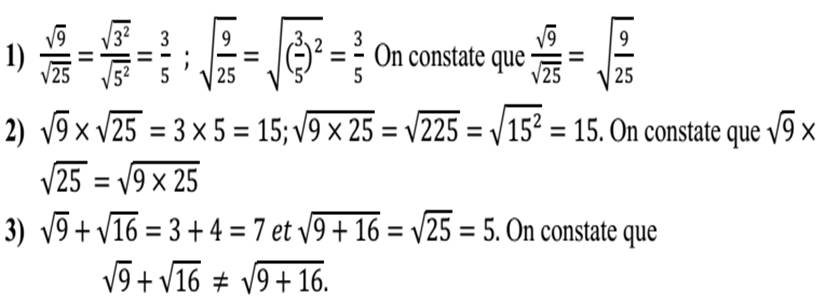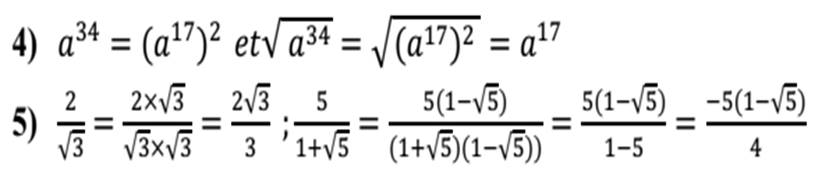RACINES CARRÉES
DEFINITION
Pour
tout nombre réel positif a, la racine de ce nombre est le nombre réel positif
dont le carré est égal à a.
Il est noté : Ѵa
Le symbole Ѵ est appelé radical.
Exemple :
Ѵ25= 5 car 25=5x5
Ѵ36= 6 car 36=6x6
NB : La racine carrée d’un nombre négatif n’existe pas (du moins
dans l’ensemble des réels).
PROPRIETES
-Pour tout a≥0, x2=a <=> x=Ѵa ou x=-Ѵa
Exemple : x2 = 12.
=> x = -Ѵ12
ou
x =+Ѵ12
-Pour
tout a,

Exemple :
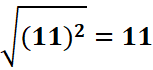

-Quelque soient les nombres a et b
positifs :
![]()
Exemple :![]()
36 ≤ 49
=> Ѵ36 ≤ Ѵ49
-
Quelque soient les nombres a et b positifs :
![]()
Exemple :
![]()
-
Quelque soient les nombres A et B positifs avec B![]() 0:
0:
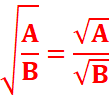
Exemple :
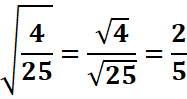
OPERATIONS SUR LES RACINES
CARREES
Simplification
· ![]() =
=![]() =
= ![]() x
x![]() =2
=2![]()
· ![]() =
=![]() =
=![]() =20
=20
·
![]() .
.![]() =
= =
=![]() =
=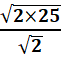 =
= =5
=5
Conjugaison
Pour écrire une fraction sans radical au
dénominateur on multiplie le numérateur et
le dénominateur par l’expression conjuguée du dénominateur.
Exemples :
1.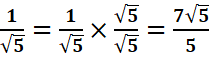
2.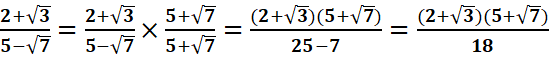
Les nombres qui peuvent s’écrire sous la forme
√a sont
des nombres irrationnels, ils peuvent avoir une partie décimale est illimitée.
EXERCICES
EXERCICE I:
a-Simplifier l’écriture des
expression suivantes :
![]()
![]() ;
; ![]()
b-Ecrire simplement : ![]()
c-Donner l’expression conjuguée des expressions
suivantes :
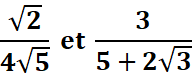
d-Calculer :
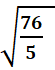 x
x :
:
EXERCICE II
:
1.Ecrire le plus simplement
possible :
![]()
![]()
2.Calculer  et
et ![]()
3.Rendre le dénominateur
rationnel(conjugaison)
 et
et 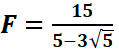
EXERCICE III:

CORRIGES :
EXERCICE I:
a- ![]()
![]()
![]() - 7
- 7![]() +
+![]()
=6![]() -7
-7![]() +
+![]()
= 6![]() -7
-7![]() +
+![]()
=![]() =13
=13![]()
b-![]() =
=![]() x
x![]() =
=![]() 2 x
2 x![]()
c- =
=![]() x
x![]() =
=![]() =
=![]()
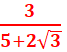 =
=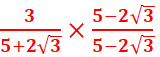 =
= =
=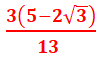
d- x
x =
= =
=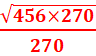
![]() :
: =
= =
=![]() =
= =
=
EXERCICE II:
![]() +
+![]() -
- ![]() -
-![]()
=![]() 2 +
2 + ![]() 2 -
2 -![]() 2 -
2 - ![]() 2 = -
2 = -![]() 2
2
![]() +
+ ![]() -
- ![]() = 4
= 4![]() 5
5![]()
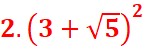 =
=![]()
=![]() =
=![]()
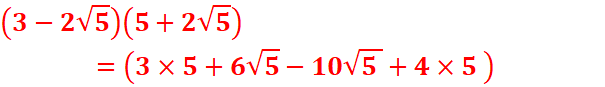
=![]() - 4
- 4![]()
![]()
 =
=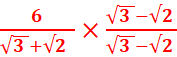 =
= =
=![]()
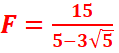 =
=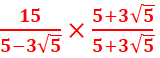 =
=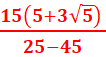 = -
= - 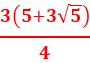
EXERCICE III :