FONCTION LOGARITHME
NEPERIEN
DEFINITION ET PROPRIETE
Définition
On appelle fonction logarithme népérien, la primitive sur
l’intervalle![]() de la fonction
de la fonction 
notée lnx
et prenant la valeur 0 en 1.
f: ]0,→[ → IR
x →f(x)=lnx
Remarques :
·
ln(1)=0
·
ln(e)=1 ou e est la base du logarithme (e=2,718)
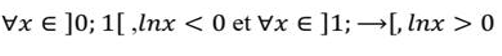
Propriétés
1) Domaine
de définition.
Soit U une fonction définit sur son
domaine de définition,
·
ln(U(x)) existe si et seulement si U(x)>0
·
ln|U(x)| existe si et seulement si U(x)≠0
2) pour tous les
nombres réels a et b strictement positifs on a :
·
![]()
·
![]()
·
![]()
·
![]()
·
![]()
·
![]()
·
![]()
EQUATIONS ET
INEQUATIONS COMPORTANT LA FONCTION (lnx)
METHODE
Pour
résoudre les équations (resp les inéquations)
comportant, on procède comme suit :
-On détermine l’ensemble de validité
(contrainte sur l’inconnue)
-On transforme l’équation (resp l’inéquation) sous la forme,
lna=lnb <=>a=b
(resp lna≤lnb
<=> a≤b )
- On résout l’équation (resp l’inéquation) et on
détermine l’ensemble solution en
tenant compte de l’ensemble de validité.
NB : on pourra faire un changement
de variable dans certain cas en posant :X=lnx
DERIVEÉS ET PRIMITIVES
Dérivée
. Soit U une fonction dérivable et
strictement positive sur un intervalle I. la fonction ln est dérivable sur I et
on a :
·
![]()
·
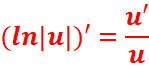
Primitive
soit u une fonction dérivable et
ne s’annulant pas sur un intervalle I.
La fonction ![]() admet pour primitive sur I la
fonction :ln|u| +k, k étant un
nombre réel.
admet pour primitive sur I la
fonction :ln|u| +k, k étant un
nombre réel.
Limites de références
Les limites
classiques ou limites de références sont admises :
·
![]()
·
![]()
·
![]()
·
![]()
·
![]()
·
![]()
·
![]()
·
![]()
Pour tout
nombre réel α>0
Etude
de la fonction lnx
·
Domaine de définition
:
· ![]()
Limites :
![]()
![]()
Dérivée et sens de variation :
ln est dérivable sur
· 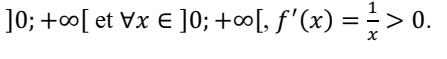
Donc la fonction ln est strictement croissante.
Tableau de variation :
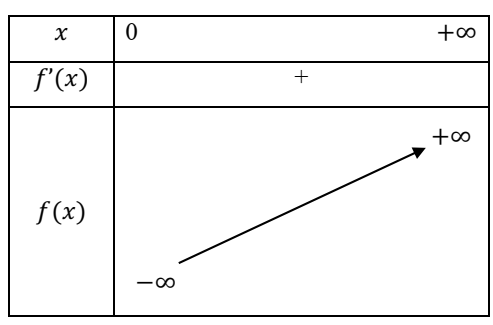
·
Branche
infinie :
 donc la courbe admet une branche
donc la courbe admet une branche
parabolique de direction (OI)
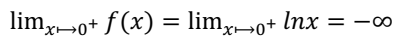
Donc la droite x=0 est asymptote verticale à la courbe
de f
·
Points
d’intersection avec les axes :
 donc la courbe de coupe l’axe des
donc la courbe de coupe l’axe des
abscisses en
·
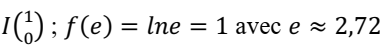
Equations des tangentes aux points
![]()
![]()
·
![]()
Construction de la courbe ( ) de :
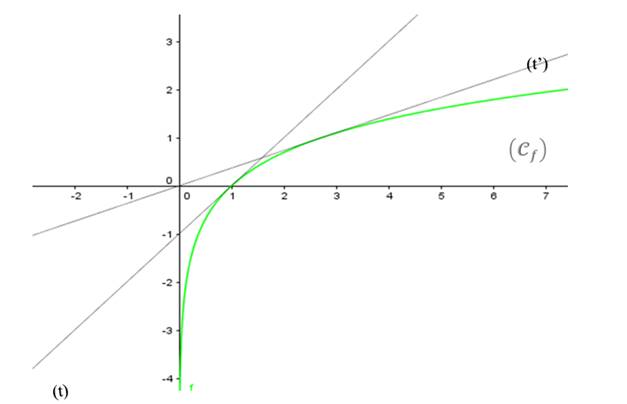
LOGARITHME DE BASE a
Définition
et propriété
Définition : soit à ϵ ]0 ;1 [ ⋃ ]1 ;+∞
[ on appelle logarithme de base la fonction notée loga et définie par :
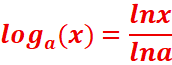
Remarque :
R1:
si a=e , alors loge(x)=![]() =lnx
=lnx
R2: si a=10 ,
alors log10(x)=![]() =logx (logarithme décimal)
=logx (logarithme décimal)
Propriétés : le logarithme de base possède les mêmes propriétés que la fonction
logarithme
népérien.
·
![]()
·
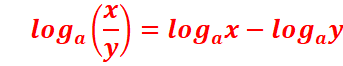
·
![]()
·
![]()
·
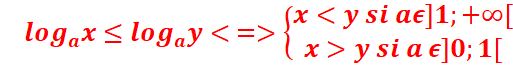
EXERCICES
EXERCICE
I : Déterminer l’ensemble
de définition de chaque fonction f
a.![]()
b. ![]()
c. 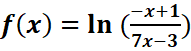
d ![]()
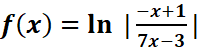
EXERCICE II : Calculez les limites des fonctions
suivantes :
a.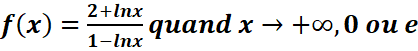
b. 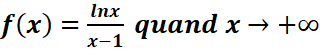
c. ![]()
d. 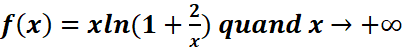
EXERCICE
III :
Calculez les dérivés des fonctions suivantes :
a. ![]()
b. 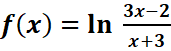
c. ![]()
d. ![]()
EXERCICE IV: Cochez la bonne réponse.
1-La dérivée de la
fonction :
f(x)=ln(x2 + 1) est :
a) -3 b) -3x
c) -3/ln(-3x+1) d) pas de
bonne réponse
2-Une primitive de la
fonction :
f(x)=x/(x2+1):
a) ln(x2 + 1) b) 1/2ln(x2 +
1) c) 2 ln(x2 +
1) d) =1/2(x2+1)
3-Le domaine de
définition de la fonction :
f(x)= 1/2ln(x2 + 1)
est :
a) R b) R\{1} c) R\{-1} d) R*
4-La valeur de ꭍ12 1/x dx est :
a)1/2
b) ln2 c)
-1/2 d)-ln2
5-La solution de
l’inéquation ln(x + 4) > ln(2x-1) est :
a)]1/2 ;5[ b)]-∞ ;5[ c)]-4 ;1/2[ d) aucune bonne réponse
EXERCICE
V :
Calculez les primitives des fonctions suivantes :
a. 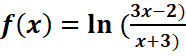
b. 
c. 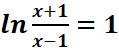
EXERCICE VI : Résoudre dans IR
a. ![]()
b. 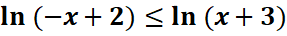
c. ![]()
d. 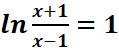
EXERCICE VII :
1-Trouver deux nombres réels a et b tels que
pour tout x réel,
P(x)= -x3 + 2x2+x-2=
(x2-1)(ax + b),
Déterminer les solutions de l’équation P(x)=0.
2-En
déduire dans R les solutions des équations suivantes :
a)
- (lnx)3 + 2(lnx)2
+ lnx - 2 =0
b)
-e3x + 2e2x +ex
-2 = 0
EXERCICE VIII:
1-a) Résoudre dans IRxIR
le système suivant :
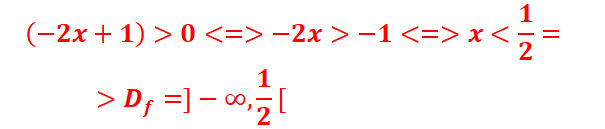
b) En déduire les solutions dans IRxIR du système suivant :
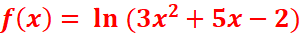
2-
Résoudre dans R, l’équation (E) :
a)
X2
- 4X +3 =0.
b)
En
déduire les solutions de l’équation :
ln2x _4lnx+3=0
CORRIGES
EXERCICE I : Déterminer l’ensemble de définition de chaque
fonction f
a.![]()
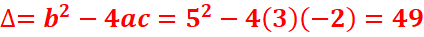
b. ![]()
![]()
![]()
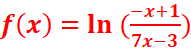
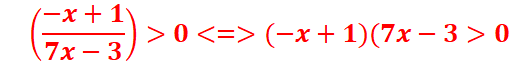
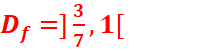 //Une équation de la forme ax2+ bx
+ c=0 est du signe de a
a l’extérieur des racines, ici a=3>0
donc ax2+ bx + c>0
//Une équation de la forme ax2+ bx
+ c=0 est du signe de a
a l’extérieur des racines, ici a=3>0
donc ax2+ bx + c>0
c. 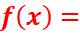
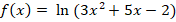
|
x |
-∞ 7/3 1 +∞ |
|||
|
-x+1 |
+ |
+ |
- |
|
|
7x-3 |
- |
+ |
+ |
|
|
f(x) |
- |
|
+ |
- |
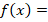 //Une équation de la forme ax2+ bx
+ c=0 est du signe de -a
a l’intérieur des racines, ici
a=-1<0 donc ax2+ bx + c<0
//Une équation de la forme ax2+ bx
+ c=0 est du signe de -a
a l’intérieur des racines, ici
a=-1<0 donc ax2+ bx + c<0
d ![]()
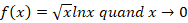
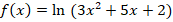 //
//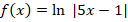
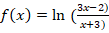
EXERCICE
II : Calculez les limites des
fonctions suivantes :
a.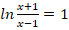
· 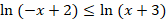
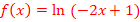
=>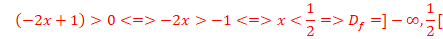
· 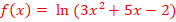
· 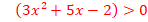
· 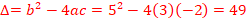
|
x |
0 e +∞ |
||
|
1-lnx |
|
|
|
b. 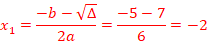
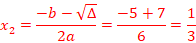
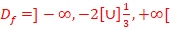 //
//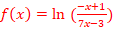
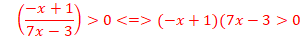
c. ![]()
![]()
On pose t=Ѵx
=>x=t2=>Ѵxlnx=2tlnt lorsque x→0,
t→0
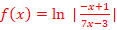
d. 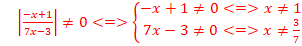
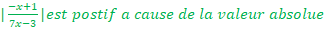
On pose X=2/x =>x=X/2,
Lorsque x→+∞, X→0
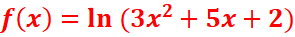
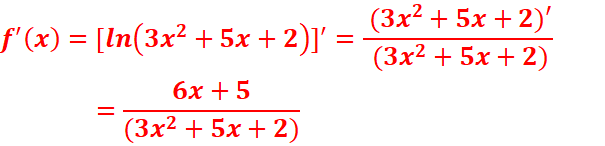 //car
//car 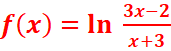
EXERCICE III : Calculez les dérivés des fonctions
suivantes :
a. ![]()
Df=]-1/3 ;2[
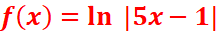
b. 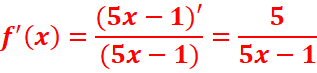
Df=]-∞ ;-3[U]2/3 ;+ ∞[

c. ![]()
Df=]-∞ ;1/5[
U ]1/5 ;+ ∞[

d. ![]()

EXERCICE IV: Cochez la bonne réponse.
1-La dérivée
de la fonction :
f(x)=ln(x2 + 1) est : c) -3/ln(-3x+1)
2-Une primitive
de la fonction :
f(x)=x/(x2+1)
est: b) 1/2ln(x2 +
1)
3-Le domaine
de définition de la fonction :
f(x)= 1/2ln(x2 + 1)
est : a) R
4-La valeur
de ꭍ12 1/x
dx est : b) ln2
5-La solution
de l’inéquation ln(x + 4) > ln(2x-1) est :
a)]1/2 ;5[
EXERCICE V : Calculez les dérivés des
fonctions suivantes :
a. 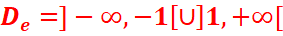
F(x)=ln|![]() |
|
b.  =
=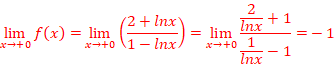
F(x)=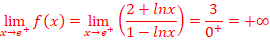
c. 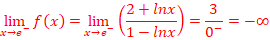 =
=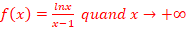
F(x)=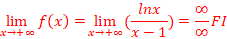
EXERCICE VI :
a. ln(-2x+1)=ln(x+4)
Domaine d’étude : 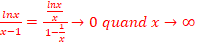
ln(-2x+1)=ln(x+4)<= >-2x+1=x+4 <=
>x=-1 =>S={-1} //-1 appartient bien au domaine d’étude De.
b. 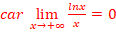
Domaine d’étude : 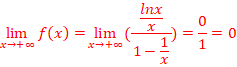 =>
=>![]()
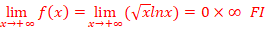
S={![]() )
)
c.
![]()
Domaine d’étude : 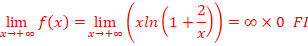
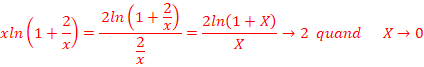
=>S=]-3,-1/2[
d.![]()
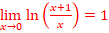
=>S=]-3,2[
EXERCICE VI :
1-Trouver
deux nombres réels a et b tels que pour tout x réel,
P(x)= -x3 + 2x2+x-2= (x2-1)(ax + b),
-x3 + 2x2+x-2= (x2-1)(ax + b)=ax3 +bx2
-ax -b
Par identification,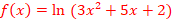
P(x)= (x2-1)(-x + 2)=0=>(x2-1)=0 ou (-x + 2)=0 =>x=-1,1 ou
2.
2-En déduire dans R les solutions des équations suivantes :- (lnx)3 + 2(lnx)2 + lnx - 2 =0
On
pose :X=lnx
L’équation
devient : -X3+2X2+X-2=0
X=lnx=-1=> x=e-1
X=lnx=1=> x=e
X=lnx=2=> x=e2
EXERCICE VII:
1-a) Résoudre dans IRxIR le système suivant :
2x + 5y=19
x + y= 5
x + y=
5=>y=5-x
2x+5(5-x)= 19 < =>2x-25-5x=19< =>-3x=-6=>x=2
y=5-2=3
b) En déduire les solutions dans IRxIR du système suivant :
lnx2 + lny5=19 2lnx+5lny=19 2lnx+5lny=19
lnx4 + lny4 = 20 < => 4lnx+4lny=20 < =>
lnx+lny=5
on
pose :X=lnx et Y=lny
le système
devient : 2X + 5Y=19
X + Y= 5
=> X=lnx =2
=> x=e2
Y=lny=2 =>y=e3
EXERCICE VIII:
1-a)
Résoudre dans IRxIR le système suivant :
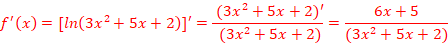
y=5-x
2x+5(5-x)=19
-3x=-6 =>x=2 et y=3
b) En
déduire les solutions dans RxR du système
suivant :
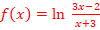 < = >
< = >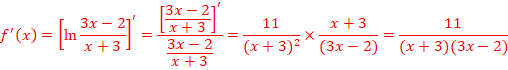 < = >
< = >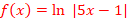
On pose : X=lnx et Y=lny
Le système devient :
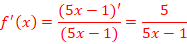
lnx=2 =>x =e2
lny=3 =>y=e3
2- Résoudre dans R, l’équation
(E) :
a)
X2
- 4X +3 =0.
Δ=16-12=4
X1=(4-2)/2=1
X2=(4+2)/2=3
b)
En
déduire les solutions de l’équation :
ln2x
_4lnx+3=0
on pose : X=lnx e
lnx1=1=>x1=e et lnx2 =3
=>x2=e3