NOTION DE QUANTITE DE
CHALEUR.
NOTION D’ENERGIE.
Définition.
L’énergie est une grandeur physique qui
représente la capacité d’un corps ou d’un système à :
-
Déformer
ou déplacer un corps.
-
Élever
la température ou changer l’état physique d’un corps.
L’unité de l’énergie dans le SI est le joule
(j), il existe d’autres unités tel que le wattheure (Wh) et 1Wh = 3600j.
Les
différentes formes d’énergie.
L’énergie existe sous plusieurs formes qui peuvent se transformer d’une
à l’autre, les principales formes sont : L’énergie électrique, mécanique
(énergie potentielle de pesanteur, énergie élastique, énergie cinétique),
chimique, nucléaire, calorifique…
L’énergie calorifique se manifeste sous forme de chaleur.
NOTION DE CHALEUR.
Effets des
échanges de chaleur.
Le transfert de chaleur
peut avoir pour effet :
-
De
faire varier la température d’un corps ou système.
-
De
provoquer un changement d’état physique.
-
De
favoriser une réaction chimique.
Modes de
transfert de chaleur.
Les
échanges de chaleurs peuvent se faire soit par :
-
La conduction : C’et la propagation
de la chaleur d’un point à un autre, (bâton en fer chauffé, la chaleur se
propage tout au long de celui-ci),
-
La
convection : C’est le mouvement pris par un fluide dû aux différentes
températures ente les différentes parties du fluide (une eau chauffée, la
partie inférieure chauffée monte donnant place à celle supérieure),
-
Le
rayonnement (une eau dans un verre et placé au soleil s’échauffe grâce au
rayonnement du soleil).
Mesure des quantités de chaleur
Pour mesurer les quantités de chaleur, généralement on utilise des
appareils appelés calorimètres. Ceux-ci sont des récipients fermés dont
les parois sont constituées d’isolent thermique. Ces parois ne
permettent pas d’échanges de chaleur avec l’extérieur : Les calorimètres
sont donc considérés comme des enceintes adiabatiques(les échanges de chaleur entre
l’intérieur et l’extérieur sont presque nuls).
Les
calorimètres généralement utilisés en laboratoire sont le calorimètre de
Berthelot et le calorimètre de Dewar.
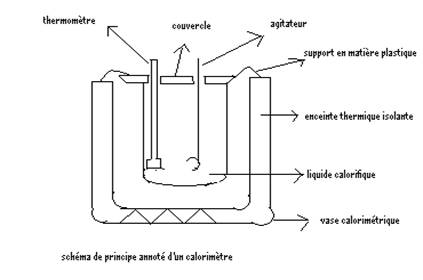
Principe des échanges de chaleur.
Lorsque plusieurs corps
sont dans une enceinte adiabatique, la somme algébrique des quantités de
chaleur échangées pour atteindre l’équilibre thermique est nulle :
∑Q = 0
Expression de la quantité de chaleur échangée par
un corps ne subissant pas de changement d’état.
L’expérience montre qu’au cours de l’échauffement
d’un corps, la quantité de chaleur Q reçue par celui-ci est proportionnelle à
sa masse et à la variation de sa température. Ainsi, m représentant la masse de
ce corps, et Δθ la variation de température
subit par le corps, nous aurons
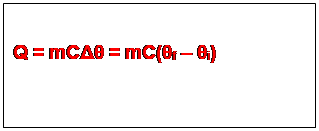
.
C est une constante qui
dépend de la nature du corps et est appelée chaleur massique de la
substance constituant le corps.
Exemple : CH2O=4190j/kg/K
![]() représente la
variation de température en kelvin(K)
représente la
variation de température en kelvin(K)
M est la masse du corps en kilogramme (kg)
Q est la quantité de chaleur en joules(J)
Relation
entre le degré Celsius et le degré kelvin
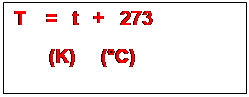
Remarques :
-
Il
existe une autre unité pour la quantité de chaleur : La calorie (cal) et 1cal = 4,18j.
Dans l’expression Q = mC(θf – θi),
le produit mC généralement noté K est appelé capacité thermique ou capacité
calorifique du corps considéré d’où

Capacité
thermique d’un calorimètre.
Généralement, le
calorimètre participe aux échanges thermiques. Il faut donc prendre en compte
la valeur de sa capacité thermique C ou K.
Expression de
la quantité de chaleur échangée par un corps qui subit un changement d’état.
La matière se présente
sous trois états physiques à savoir, l’état solide, liquide et gazeux. Très
souvent, pour passer d’un état à un autre, la matière peut :
-
Soit
céder de la chaleur au milieu extérieur,
-
Soit
en recevoir.
On appelle chaleur latente de fusion
d’un corps pur généralement noté Lf, la quantité de chaleur à fournir à l’unité de
masse de ce corps pris à sa température de fusion pour l’emmener entièrement à
l’état liquide. Cette transformation s’effectue à température constante.
Dans le SI, la chaleur latente s’exprime en
j/kg. Dans le cas où l’on veut faire fondre une masse m d’un corps pris à
sa température de fusion, la quantité de chaleur nécessaire pour la fusion
totale de ce corps est donnée par la relation
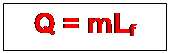 ,
,
Q en joules(J)
m en
kilogramme (kg).
Lf en
joules par kilogramme(Jkg-1)
On appelle chaleur latente de vaporisation d’un corps pur notée Lv, la quantité de chaleur qu’il
faut fournir à
l’unité de masse
de ce corps pur pris à la température de vaporisation pour l’emmener entièrement à l’état vapeur. Pendant
ce changement la température reste constante. La chaleur latente de
vaporisation s’exprime en j/kg. Ainsi, pour vaporiser entièrement un liquide de
masse m pris à sa température de
vaporisation, la quantité de chaleur nécessaire donnée par la relation
![]()
Q en joules(J)
m en kilogramme (kg).
Lv en joules par kilogramme(Jkg-1)
EXERCICES
EXERCICE I :
Calculer la quantité de chaleur nécessaire pour porter une
masse d’eau de 300g, initialement à 25°C à une température finale de 35°C.
On donne la chaleur massique de l’eau : 4190 J.kg-1.K-1.
EXERCICE II :
On mélange dans une enceinte adiabatique 5L
d’eau à
EXERCICE III :
Un calorimètre contient une masse d’eau 200g à la
température 18°C. On y ajoute une certaine quantité d’eau tiède de masse 100g
et de température 25°C. A l’équilibre thermique, la température du mélange est
20,3°C.
1-Quelle est l’expression de la quantité de chaleur reçue
par le système qui s’échauffe ?
2-Quelle est l’expression de la quantité de chaleur perdue
par le système qui se refroidit ?
3-En déduire la capacité calorifique du calorimètre.
EXERCICE IV :
1. Déterminer la quantité de chaleur nécessaire
pour faire fondre une masse de 30 g de glace pris à 0°C.
On donne
Lf = 335j/kg.
2. On désire chauffer une masse d’eau de 300g, initialement
à 25°C, jusqu’à la vaporisation. L’eau passe de l’état solide à l’état vapeur à
100°C sous la pression atmosphérique. Calculer la quantité de chaleur reçue par
cette masse d’eau sachant que la chaleur latente de vaporisation de l’eau est
de 2,25.106 J.kg-1.
3.Quelle quantité de chaleur faut-il fournir à
un morceau de plomb de masse m=200g, pris à la température θ1=25°C, pour le
porter à la température
θ2=375°C.
On donne :
-température de fusion du plomb : θf=327°C ;
-chaleur latente de fusion du plomb : Lf=26,3.![]() J.kg-1.
J.kg-1.
-chaleur massique du plomb à l’état
solide : cs=129J.kg-1. °C-1.
--chaleur massique du
plomb à l’état liquide : cL=142J.kg-1.°C-1.
EXERCICE V :
Situation
problème
L'étain est un corps solide à
température ambiante. Il est utilisé pour la soudure des composants
électroniques.
Jean technicien de réparation des appareils électroniques, projette d'utiliser
le dispositif ci-contre constitué de deux thermoplongeurs pour faire fondre 100
g de morceaux d'étain pris à 20'C en moins de 5,0 s afin de respecter le timing
de dépannage imposé par les clients. Jean est préoccupé et se demande si le
dispositif sera à mesure de le satisfaire.
Par ailleurs compte tenu des contraintes financières, l'utilisation de ce
dispositif n'est possible que si le coût en énergie électrique est négligeable ( c'est-à- dire inférieur à 1 Fcfa symbolique
) en 10 s d'utilisation.
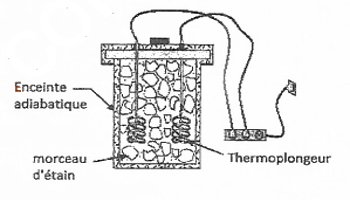
Document
1 : Caractéristique du système constitué par les deux thermoplongeurs.
Rendement est η=0,80
Puissance calorifique ( utile) Pc = 2,0 kw
Document 2 : Coût énergétique
1kW.h = 3,6 405i
1kW.h coûte 75 Fcfa
Document 3 : Propriétés physiques de l'étain
Malléable et résiste à la corrosion.
Température de fusion :Tf = 232°C
Chaleur massique : C = 228 J/kg.K
Chaleur latente de fusion : Lf = 6000
J/k
En exploitant les informations ci-dessus et en utilisant une démarche
scientifique,
1 -Examine la préoccupation de Jean sur la capacité du dispositif à le
satisfaire.
2- Examine sur le pian financier s'il est possible d'utiliser ce
dispositif.
EXERCICE
VI :
Situation problème : Vérification de la pureté du fer
Pour la construction d'un immeuble, un entrepreneur souhaite acheter du fer à
Béton. Pour s'assurer de la pureté de celui-ci, il a contacté le laboratoire de
physique d'un collège avec un échantillon d'un kilogramme dudit fer. Ce
laboratoire, dispose d'un calorimètre jamais utilisé dont la valeur en eau
marquée est μ=18,2 g, on y trouve aussi des dispositifs pour
chauffer ou refroidir des corps. L'enseignant responsable du laboratoire a
réalisé les deux expériences suivantes :
Expérience 1 :
Dans ce calorimètre contenant initialement 200 g d'eau à la température de
25,3°C, on verse 300 g d’eau à la température de 17,7 °C. On observe que la
température du mélange se stabilise à 20,9°C.
Expérience 2 :
Dans le même calorimètre contenant 500 g d’eau à 20,9 °C, on plonge le bloc de
fer à la température de 48°C. La température se stabilise à 14,2 °C.
Chaleur massique de l'eau ce=419o J.kg/C, chaleur massique du fer
pur cFe= 470 J/kg.K
En exploitant les informations ci-dessus,
1 Prenez position sur la valeur en eau u qui est marquée.
2 À l'aide d'un raisonnement scientifique, prononcez-vous sur l'état de pureté
du morceau de fer afin de permettre à l’entrepris de se décider sur la
commande.
CORRIGES :
EXERCICE
I :
Q = mCΔθ
= mC(θf – θi)=0,3x4190(35-25)=12570J.
NB : Une calorie
(cal) correspond à 4,186 joules(J) => Q=![]() =3000 cal.
=3000 cal.
EXERCICE
II :
Système qui se réchauffe : V1=5
l, θ1=25°C
Système qui se refroidit : V2=7 l, θ2=60°C
Équilibre : θf
![]() = m1c(θf -25)=5x4190(θf-25)
= m1c(θf -25)=5x4190(θf-25)
![]() = m2c(θf-60) =7x4190(θf – 60)
= m2c(θf-60) =7x4190(θf – 60)
A l’équilibre,![]() ó5x4190(θf-25)
+ 7x4190(θf – 60)=0
<=>5(θf-25) + 7(θf
– 60)=0 =>12 θf=545
=> θf=45,4°C
ó5x4190(θf-25)
+ 7x4190(θf – 60)=0
<=>5(θf-25) + 7(θf
– 60)=0 =>12 θf=545
=> θf=45,4°C
EXERCICE
III :
Système qui se réchauffe : m1=200
g, θ1=18°C
Système qui se refroidit : m2=100g,
θ2=25°C
Équilibre : θf=20,3C
1.![]() = (m1c+ K)Δθ =( mC+K)(θf – θ1)
= (m1c+ K)Δθ =( mC+K)(θf – θ1)
2.![]() = m2cΔθ =m2c(θf – θ2)
= m2cΔθ =m2c(θf – θ2)
3.A l’équilibre,![]()
![]() ( m1c+K)(θf – θ1)
+ m2c(θf
– θ2)=0
( m1c+K)(θf – θ1)
+ m2c(θf
– θ2)=0
=> K=![]() - m1c =
- m1c =![]() – 0,2.4190=18,2 JC-1
– 0,2.4190=18,2 JC-1
EXERCICE
IV :
1. On sait que Q = mLf = 30x10-3x335=100,5 J
2. Il faut de la chaleur pour élever
la température de 25 à 100°C plus de la chaleur pour le passage de l’état
liquide à l’état vapeur.
Q=mc (θf
– θ1) +mLv = 0,3.4190(100-25)
+ 0,3.2,25.106=778702,5J.
3. Q=mcs(θf – θ1) +mLf +mcL
(θ2 – θf)
= 0,2x129 x(327 – 25) +0,2x26,3.![]() +0,2x142 (375 – 327f)=1,44.
+0,2x142 (375 – 327f)=1,44.![]() J.
J.
EXERCICE V :
Situation problème
1. Il est question ici de vérifier si le dispositif permettra à jean de faire
fondre 100 g d’étain pris à 20°C en 5,0 s.
Pour cela nous allons :
• Exprimer la quantité de chaleur totale Q permettant la fusion de 100g d’étain
pris à 20°C.
• Déterminer la durée t nécessaire au dispositif pour fondre 100g d'étain pris
à 20°C.
• Comparer cette durée à 5,0 s et conclure.
Expression de la quantité de chaleur totale
Q=mLf+ mC(Tf−Ti)
Détermination du temps t
Q=W=PC.t ⇒t= mLf+mC(Tf−Ti)PC
AN : t=2,72s
t=2,72s≺5s la durée de fusion de l’étain dans le dispositif est
inférieur à celle acceptable par Jean.
Ce dispositif peut satisfaire Jean
2. Il est question ici d'évaluer le coût financier en énergie électrique pour
10s de fonctionnement de ce dispositif afin de valider ou non son utilisation.
Pour cela nous allons:
• Détermination de l'énergie électrique consommée par le dispositif en 10 5,.
• Estimer du coût énergétique du dispositif,
• Comparer ce coût 1Fcfa et conclure. A
Détermination de l'énergie électrique consommée par le dispositif en 10 s.
η=PCP avec P=Wt
W=t.PCη
W=25000J= 6,94×10−3kWh
Estimation du coût énergétique du dispositif.
C≺1Fcfa, le coût énergétique de ce dispositif est négligeable pour
une durée d'utilisation de 10 s
Ce dispositif est utilisable.
EXERCICE VI :
SITUATION PROBLÈME : Vérification de la pureté du fer
Prise de position sur la valeur en eau μ
Le problème posé est de vérifier si la valeur en eau marquée sur le calorimètre
jamais utilisé est exacte.
Pour cela, nous allons :
• Déterminer les quantités de chaleur échangées par les différentes parties
du système.
• Appliquer le principe des échanges de chaleur pour déterminer la valeur en
eau, la comparer à celle marquée sur le calorimètre et conclure.
Quantité de chaleur échangée par le calorimètre et son contenu
: Q1=(m1+μ) CeΔθ
Quantité de chaleur échangée par l’eau ajoutée : Q2=m2CeΔθ′ 0.5pt
D'après le principe des échanges de chaleur :
Q1+Q2=0 Q1+Q2=0 ⇒μ= m2Δθ′Δθ−m1
AN : μexp=18,18g ≈18,2g=μth 0,5 pt
La valeur en eau marquée sur le calorimètre jamais utilisé est correcte car la
valeur expérimentale est sensiblement égale à la valeur théorique.
2 Avis sur l'état de pureté du fer
Le problème posé est de vérifier la pureté du fer à béton afin d'orienter
l'entreprise dans sa commande.
Pour cela, nous allons :
• Déterminer les quantités de chaleur échangées par les différentes parties
du système.
• Appliquer le principe des échanges de chaleur pour déterminer la chaleur
massique du fer, la comparer à celle donnée par la littérature et conclure.
Quantité de chaleur échangée par le calorimètre et son contenu :
Q=(m+μ)CeΔθ′
Quantité de chaleur échangée par le fer : QFe=mFeCFeΔθ′′
D'après le principe des échanges de chaleur :
Q+QFe=0⇒ CFe= (m+μ)Δθ′mFeΔθ′′
AN : CFe=451,78J /Kg/K
CFe=451,78J /Kg/K ≠ 470J /Kg/K
L’entreprise ne doit pas passer la commande car le fer à béton n'est pas pur.
Avez-vous un exercice à proposer ?Cliquez-ici
Merci de votre visite
Laissez un commentaire