REPRÉSENTATION GRAPHIQUE D’UNE FONCTION
BRANCHES INFINIES D’UNE
REPRESENTATION GRAPHIQUE
Asymptote verticale
Lorsque la fonction f(x) tend vers l’infini quand x tend
vers a, la droite d’équation x=a est asymptote verticale.
Exemple :
![]() ,
,
![]() => la droite y=1 est asymptote verticale.
=> la droite y=1 est asymptote verticale.
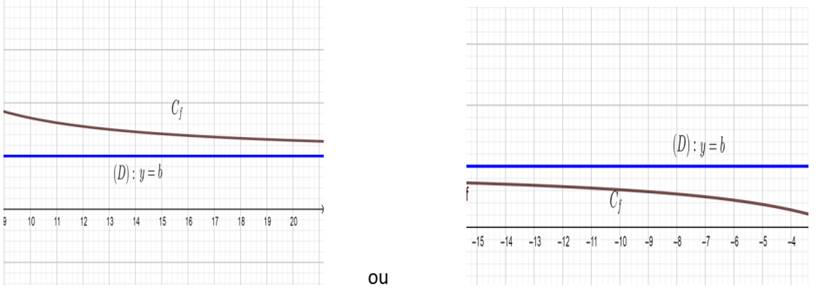
Asymptote horizontale
Lorsque la fonction f(x) tend vers un nombre b quand x tend
vers l’infini, la droite d’équation y=b est asymptote horizontale.
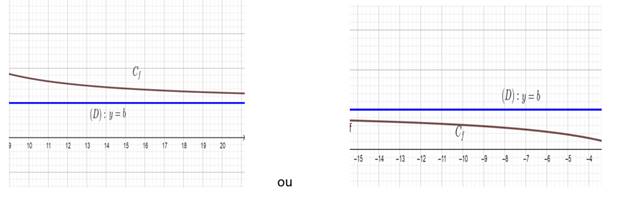
Exemple :
![]() ,
,
![]() => la droite y=2 est asymptote
horizontale.
=> la droite y=2 est asymptote
horizontale.
Asymptote oblique
La droite y=ax + b
est une asymptote oblique à la courbe en ![]() si
si ![]() = 0.
= 0.
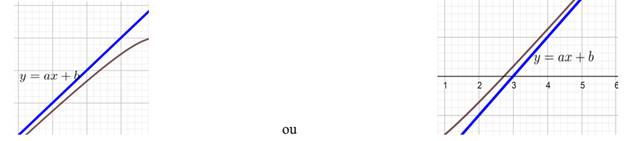
Exemple : ![]()
f(x) peut s’écrire sous
la forme ![]() +
+![]()
![]()
![]() =>
la droite y=x-1 est asymptote oblique.
=>
la droite y=x-1 est asymptote oblique.
Branches paraboliques
Lorsque la fonction f(x) tend vers l’infini quand x tend
vers l’infini, la courbe Cf représentative de la fonction admet une
branche parabolique.
Si ![]() =
+
=
+![]() alors la courbe admet une branche parabolique.
alors la courbe admet une branche parabolique.
· ![]() => la courbe admet une branche parabolique
de direction (O, I).
=> la courbe admet une branche parabolique
de direction (O, I).
· ![]() => la courbe admet une branche parabolique
de direction (O, J).
=> la courbe admet une branche parabolique
de direction (O, J).
Position relative de la courbe par
rapport à son asymptote
La position relative entre deux courbes Cf et
Cg est donnée par le signe de la différence f(x)-g(x).
·
Si
f(x)-g(x)>0 sur l’ensemble I, Cf est au-dessus (strictement) de Cg sur cet
ensemble de points.
·
Si
f(x)-g(x)<0 sur l’ensemble I, Cf est au-dessous (strictement) de Cg sur cet
ensemble de points.
·
Si f(x)-g(x)=0 sur l’ensemble I, Cf coupe Cg sur cet
ensemble de points.
ETAPES
D’ETUDE D’UNE FONCTION :
1. Variations de f
Ensemble de définition
Ensemble d’étude
-parité
-périodicité
Déterminer les limites aux bornes du domaine de
définition ;
Dérivé
-déterminer f’
-signe de f’
Tableau de variation
2-Représentation graphique
Points et droites remarquables
-Asymptotes
-Tangentes
Constructions de la courbe
-table de valeurs
-choix du repère et des unités
3-Propriétés graphiques
Éléments de symétrie
-axes de symétrie
-centre de symétrie
Branches paraboliques
Points d’inflexion
EXERCICES
EXERCICE I :
Rechercher les branches
infinies de la représentation graphique des fonctions suivantes :
1. 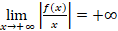
2. ![]()
3.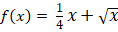
4.![]()
5. 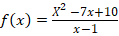
EXERCICE II : Rechercher les propriétés graphiques (éléments
de symétrie, branches paraboliques, points d’inflexion…) des fonctions
suivantes :
1. 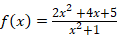
2. 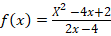
3. ![]()
EXERCICE
III : Étudier les variations des fonctions
suivantes :
1. 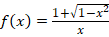
2. 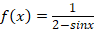
3. 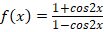
EXERCICE IV : a, b et c sont des nombres réels. On
considère la fonction f définie par :
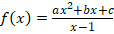 , dont le tableau de
variation est le suivant :
, dont le tableau de
variation est le suivant :
|
X |
-∞ 0 1 2 +∞ |
|
|
f’(x) |
|
-
0 + |
|
f(x) |
-∞
-∞ |
3 |
En vous aidant du tableau de variation
ci-dessus :
1-Déterminer l’ensemble de définition de f
2- Déterminer f(0), f(2) et f’(0)
3- En déduire les réels
a, b et c.
4- Déterminer
l’asymptote verticale et montrer que la droite d’équation y=x est une asymptote
oblique de la courbe Cg.
5-Construire Cg.
EXERCICE V :
On donne
la fonction définie par 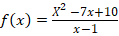
1-Donner
le domaine de définition de cette fonction
2-Etudier
les limites aux bornes du domaine de définition. Préciser les branches
infinies.
3-Montrer
que cette fonction peut s’écrire sous la forme
![]()
![]() où a, b et c sont des coefficients réels à
déterminer.
où a, b et c sont des coefficients réels à
déterminer.
4-Montrer
que la droite y=x-6 est une asymptote oblique à la courbe représentative (Cf)
de f(x).
5-Dresser
le tableau de variation de cette fonction
6-Représenter
cette fonction dans un repère orthonormé (O, i, j).
EXERCICES VI : on donne la courbe représentative
d’une fonction f(x) ci-dessous :
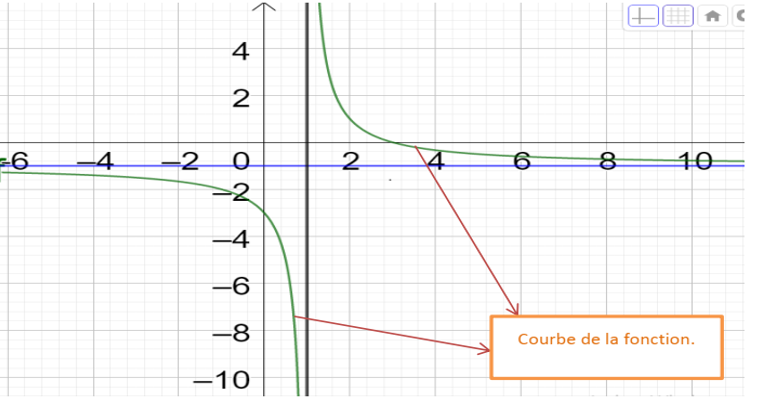
1.Determiner
en justifiant votre réponse, les équations des asymptotes a
la courbe de la fonction f.
2.

3.
![]()
CORRIGES :
EXERCICE
I :
Rechercher
les branches infinies de la représentation graphique des fonctions
suivantes :
1. f(x)=x2
![]() =>La courbe de f admet des branches
infinies
=>La courbe de f admet des branches
infinies
 => La courbe de f admet une branche
parabolique de direction (O,J)
=> La courbe de f admet une branche
parabolique de direction (O,J)
2. ![]()
![]() =>La courbe de f admet des branches
infinies
=>La courbe de f admet des branches
infinies
 => La courbe de f admet une
branche parabolique de direction (O,I)
=> La courbe de f admet une
branche parabolique de direction (O,I)
3.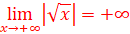
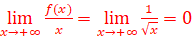 =>La courbe de f admet des branches
infinies
=>La courbe de f admet des branches
infinies
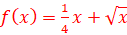
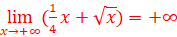 => La courbe de f admet une
branche parabolique de direction y=
=> La courbe de f admet une
branche parabolique de direction y=![]()
4.![]() +2x
+2x
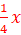
=>La
courbe de f admet une asymptote horizontale y=0
5. 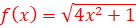
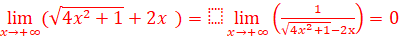
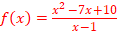
=> La
courbe de f admet une asymptote oblique d’équation y=x-6.
EXERCICE II : Rechercher
les propriétés graphiques (éléments de symétrie, branches paraboliques, points
d’inflexion…) des
fonctions suivantes :
1. 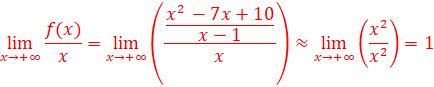
·
Ensemble de définition : Df=IR
·
Asymptote : y=2
·
Tangentes horizontales aux
points A et B abscisses respectives -2 et 1/2 (extrémums).
2. ![]()
· Ensemble de
définition : Df=![]()
·
Asymptotes : y=(1/2)x-1 et x=2
·
Centre de symétrie : point d’intersection des asymptotes.
3. f(x)=![]()
·
Ensemble de définition : Df=IR
· Ensemble
d’étude :![]()
·
Parité : impaire
·
Centre de symétrie : O
·
Point d’inflexion
EXERCICE III :
1.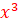
Ensemble de définition :
Contraintes :![]()
Tableau de signe
|
x |
-∞
-1
1 +∞ |
||
|
1-x2 |
- |
. + |
- |
![]()
Ensemble d’étude
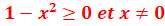 =-
=-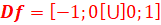 . f est impaire. On peut donc étudier f sur
]0,1] et compléter par une symétrie par rapport à O.
. f est impaire. On peut donc étudier f sur
]0,1] et compléter par une symétrie par rapport à O.
Limites
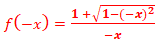 +∞
+∞
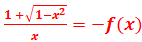 1
1
Dérivée :
f’(x)=![]()
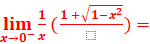
Tableau de variation
|
x |
|
|
|
|
f’(x) |
|
||
|
f(x) |
|
|
|
2.Ensemble de définition :
-1![]() ó1
ó1![]() ó
ó![]() Df=IR
Df=IR
Ensemble d’étude :
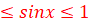 =
= . => f est périodique de période T=2п. On peut étudier f sur
. => f est périodique de période T=2п. On peut étudier f sur ![]()
Dérivée :
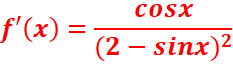
Tableau de variation :
|
x |
0 |
||
|
f’(x) |
+ |
- |
+ |
|
f(x) |
|
|
|
3. 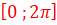
Ensemble de définition :
![]() cos2x=1 => 2x=2kп =>x=kп avec kϵZ
cos2x=1 => 2x=2kп =>x=kп avec kϵZ
f(x) est pour
tout x![]() kп , kϵZ
kп , kϵZ
Ensemble d’étude :
Périodicité : f est périodique
de période T=п. On peut réduire l’étude de f sur ![]()
Parité : f est paire donc![]() est l’ensemble d’étude.
est l’ensemble d’étude.
Dérivée : 
Tableau de variation
|
x |
0 |
|
f’(x) |
|
|
f(x) |
|
EXERCICE IV :
1- ![]()
2- f(0)=-1, f(2)=3 et f’(0)=0
3- En déduire
les réels a, b et c.
f(0)=-1 <=>![]() ,
,![]() =>c=1
=>c=1
f(2)=3 <=>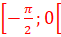 ,=3 => 4a+2b=2
,=3 => 4a+2b=2
f’(x)=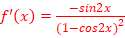
f’(0)=0 <=> =0 =>
b=-c=-1 et a=1
=0 =>
b=-c=-1 et a=1
 ,
,
4- 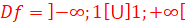 => la droite x=1 est asymptote verticale.
=> la droite x=1 est asymptote verticale.
![]() y =x est
asymptote oblique
y =x est
asymptote oblique
EXERCICE V :
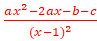
1.Domaine de définition de cette fonction
Df=![]()
2-Etude des limites aux bornes du domaine de définition.
![]()
![]()
![]()
3-Montrons que cette fonction peut s’écrire sous la forme ![]()
![]() où a, b et c sont des coefficients réels à
déterminer.
où a, b et c sont des coefficients réels à
déterminer.
![]()
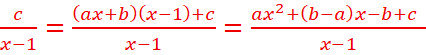 =
=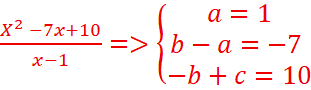
![]()
![]()
![]()
4-Montrer que la droite y=x-6 est une asymptote oblique à la
courbe représentative (Cf) de f(x).
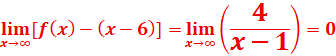
5-Tableau de variation de cette fonction
![]()
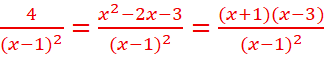
f’(x)=0 <= >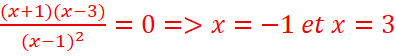
f’(x)≥0 pour tout x
appartenant a ![]()
f’(x)≤0 pour tout x
appartenant à [-1 ;3]
f(-1)=-9
f(3)=1
|
x |
-∞
-1
1 3 + |
|||
|
f’(x) |
+ |
- |
|
-
+ |
|
f(x) |
|
|
|
|
EXERCICES
VI :
1.a)
![]()
![]()
![]()
![]()
b)f’(x)=0 =>S=ø
f(x)=0 =>S={3}
f(x)=3=>S={3/2)
c) f(x)≥0 =>S=ø
f’(x)≤0 =>S=]-∞ ;1] U [1 ; +∞[
|
x |
-∞ 1 + |
||
|
f’(x) |
- |
|
-
|
|
f(x) |
|
|
|
b.
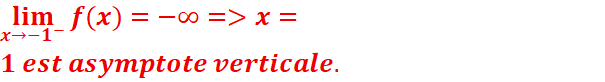

Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire