COMPARAISONS ET ENCADREMENTS
COMPARAISONS
Comparaison des entiers relatifs
Soit la droite graduée suivante :

-La distance à zéro d’un nombre décimal relatif est
ce nombre sans signe.
Exemple :la distance à zéro de -5 est 5
-Lorsque deux nombres décimaux sont positifs, le
plus grand à la plus grande distance à zéro.
Exemple : 3>2
-Lorsque deux nombres décimaux sont négatifs, le
plus grand a la plus petite distance à zéro.
Exemple : -4<-1
-Tout nombre négatif est plus petit que zéro.
Exemple : -7<0
Valeur absolue
La Valeur absolue d’un nombre relatif a est sa
distance a zéro sur la droite numérique.
La Valeur absolue se note |a| et se lit « Valeur absolue
de a »
Exemple :
|-6|=6
|+6|=6
Comparaison des rationnels
a) Si deux
fractions ont le même dénominateur la plus grande est celle qui a le plus grand
numérateur
Exemple : comparer ![]()
![]()
![]()
b) Pour comparer
deux fractions de dénominateurs différents on doit les réduire d’abord au même
dénominateur puis on applique la regle1
Exemple : comparer 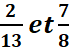
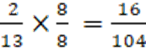

Comme ![]()
c) Pour tout réels a, b, c et d avec b et d différents
de zéro
si ![]()
Exemple :
![]()
Propriétés :

Comparaison des réels
A et B sont deux nombres positifs.

Exemples : A=2 , B=5 et C=13
2<5 =>Ѵ2<Ѵ5(si on fait racine carre de
deux termes positifs d’une inegalite, elle ne change pas).
=> (2)2<(5)2(si
on eleve au carre de deux nombres positifs d’une inegalite, elle ne change
pas).
=>2+13<5+13(si on ajoute un nombre aux deux termes positifs d’une
inegalite, elle ne change pas).
=>2x13<5x13(si on multiplie deux termes positifs d’une inegalite
par un meme nombre, elle ne change pas).
=>1/2>1/5(si on divise deux termes positifs d’une inegalite par un
meme nombre, elle ne change pas).
ENCADREMENTS
Encadrement des rationnels
Toute fraction peut s’écrire
sous la forme ![]() où q et r désignent respectivement le quotient
et le reste de la division euclidienne de a par b .
où q et r désignent respectivement le quotient
et le reste de la division euclidienne de a par b .
Un encadrement de la
fraction ![]() par deux nombres entiers naturels consécutifs
est :
par deux nombres entiers naturels consécutifs
est :
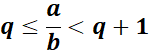
q est appelé partie
entière de la fraction .
Toute fraction peut être encadrée par
deux nombres décimaux consécutifs qui sont des quotients approchés par défaut
(le plus petit) et par excès ( le plus grand)
Exemple :a=5 et b=3
Ona : ![]()
Remarques :

Encadrement
des réels
a, b, c, d, x et y désignent des nombres positifs
tels que
a<x<b et c<y<d,
alors :
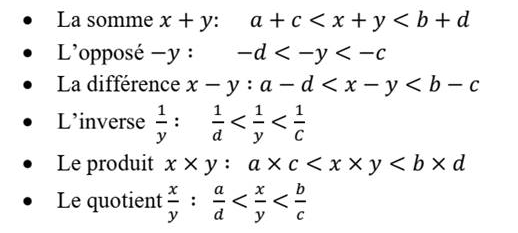
Exemples :2<x<5 et
6<y<7 alors :
2+6<x+y<5+7(si on ajoute un nombre positif aux deux termes
d’une inegalite, elle ne change pas)
-7<-y<-6
(lorsqu’on multiplie les termes d’une inegalite par-, le sens de
l’inegalite change c-a-d < devient > et vice versa).
2-7<x-y<5-6
1/7<1/y<1/6(lorsqu’on divise les termes de deux
inegalites entre eux,l’ inegalite change
de sens).
2x6<xxy<5x7(lorsqu’on multiplie les termes de deux
inegalites entre eux,l’ inegalite ne change pas).
2/7<x/y<5/6(lorsqu’on divise les termes de deux
inegalites entre eux,l’ inegalite change
de sens).
TRONCATURE ET
ARRONDI D’UN NOMBRE RATIONNEL
La troncature d’ordre
n d’un rationnel est
l’ecriture décimale de ce nombre en retenant n chiffres apprès la virgule.
Tronquer
Exemple :
Tronquer le nombre 325,49 au dixième ?
0n identifie quel chiffre représente les dixièmes,
et on supprime simplement tout ce qui est à droite. Ici le chiffre des dixièmes
est le 4. On coupe donc à cet endroit et on oublie tout ce qui est à droite des
dixièmes.
Résultat :
325,4
Arrondir
Pour arrondir un nombre, au dixième, au
centième ou au millième, il faut couper ce nombre après un, deux, ou 3 chiffres
après la virgule. Il faut analyser le chiffre qui est placé à droite de la
coupure et appliquer une des deux règles suivantes :
Règle 1 • si le
chiffre qui suit est 5, 6, 7, 8 ou 9, alors on augmente de 1 le chiffre qui
représente la référence mathématique identifiée. Arrondi par excès. Le résultat
est plus grand que le nombre original.
Règle 2 • si le
chiffre qui suit est 0, 1, 2, 3 ou 4, alors on tronque le nombre à la référence
mathématique identifiée. Arrondi par défaut. Le résultat est plus petit que le
nombre original. Les arrondis sont obtenus après avoir observé le chiffre qui suit
le rang indiqué.
Exemples :
Arrondir le nombre 325,49 au dixième ? Cet exemple correspond à la règle
1
Réponse :
arrondir le nombre 325,49 au dixième = 325,5 (arrondi par excès)
Arrondir le nombre 325,49 à l'unité ? Cet exemple
correspond à la règle 2
Réponse :
arrondir le nombre 325,49 à l'unité = 325 (arrondi par défaut)
Valeur approchée par excès et par défaut
Définition
● La
valeur approchée par défaut d’un nombre à un rang donné est sa troncature
● Pour
donner la valeur approchée par excès d’un nombre à un rang donné on rajoute 1
au dernier chiffre du nombre tronqué
Exemples :
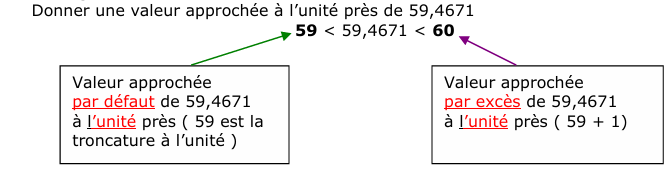
Exemple 1 : Donner une valeur approchée à l’unité près de 59,4671 59 < 59,4671
< 60 Valeur approchée par défaut de 59,4671 à l’unité près ( 59 est la
troncature à l’unité )
Exemple 2 :
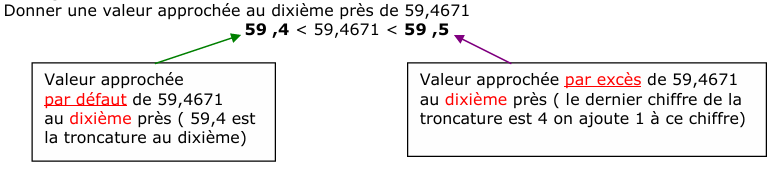
Exemple 3 :

EXERCICES
EXERCICE I :
A-Compléter les points par les
signes < ou >.
1)
56…….120
2)
2 ……..-10
3)
-34 …...-70
4)
58…….-12
5)
|-24|…..15
6)
|57|……89
B-Comparer
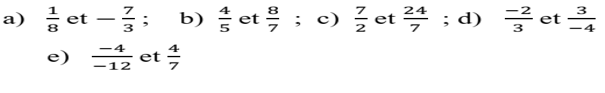
C-

EXERCICE II :
1-Sachant que x≤8
Déduire une inégalité vérifiée par chacune des
expressions suivantes :
a-x+3
b-x-7
c- -8+x
2-Completer par < ou>
a- x-1,02….x-1,002
b- 50/51+π….50/51 +3,14
EXERCICE III :
Sachant que x≥5
Déduire une inégalité vérifiée par chacune des
expressions suivantes :
1.
a- 4x
b- 0,1x
c- 2/3 x
2.
x est un nombre strictement positif. Compléter par
< ou > ;
a- 1,5x…1,05x
b-50/51xπ…..50/51x3,14
c- -3xπ ….. -3x3,14
EXERCICE IV:
1. Sachant que 1,414<Ѵ2<1,415, encadrer au dixième près le nombre ![]()
2. Sachant que 1,732<Ѵ3<1,733, donner un encadrement d’ordre 2 de 4+2![]() .
.
EXERCICE V :
1) Donner la troncature au centième des nombres
suivants : 4,258 ; 2,15895 ; 0,0001 ; 1,999 2)
La troncature au dixième du nombre x est 2,5.
Donner un encadrement aussi précis que possible de
x.
2) La troncature au dixième du nombre x est 2,5.
Donner un encadrement aussi précis que possible de x.
Donner un
arrondi au centième des nombres suivants : 4,258 ; 2,15895 ; 0,0001 ; 1,999
L’arrondi au
dixième du nombre x est 2,5. Donner un encadrement aussi précis que possible de
x.
CORRIGES :
EXERCICE
I :
A-
1) 56 <120
2) 2 >-10
3) -34 >-70
4) 58 >-12
5) |-24| >15
6) |57| < 89
B-
a)![]() =
=![]() =
=![]() et
et ![]() x
x![]() =
= ![]() =>
=>![]() =>
=>![]()
![]() x
x![]() =
=![]() et
et ![]() x
x![]() =
=![]() =>
=>![]()
c)
![]() x
x![]() =
=![]() et
et ![]() x
x![]() =
=![]() =>
=>![]() <
<![]() =>
=>![]()
d)![]() x
x![]() =
=![]() et
et ![]() x
x![]() =
=![]() =>
=>![]() =>
=>![]() <
<![]()
e)![]() x
x![]() =
=![]() et
et ![]() x
x![]() =
=![]() =>
=>![]()
C-
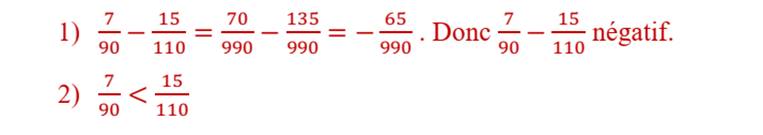
EXERCICE
II :
1.
a-
x+3<8+3 => x+3<11
b-
x-7≤8-7 => x-7≤1
c-
-8+x≤-8+8 =>-8+x≤0
2.
a- x-1,02 < x-1,002
b- 50/51+![]() > 50/51 +3,14
> 50/51 +3,14
c- -3xπ < -3x3,14
EXERCICE
III :
1.
a- x≥5 <= >4x>4x5 <= >4x≥20
b-
x≥5 <= >0,1x>0,1x5 <= >0,1x≥0,5
c- x≥5 <= >2/3x>2/3 x5
<= >2/3x≥10/3
2.
a-
1,5x > 1,05x
b-50/51xπ > 50/51x3,14
c-
-3xπ < -3x3,14
EXERCICE
IV :
1. 1,414<Ѵ2<1,415 <=>3x1,414<3Ѵ2<3x1,415
<=>4+3x1,414<4+3Ѵ2<4+3x1,415
<=> 8,242<4+3Ѵ2<8,245
2. 1,732<![]() <1,733 <=>2x1,732<2Ѵ3<2x1,733
<1,733 <=>2x1,732<2Ѵ3<2x1,733
<=>4+2x1,732<4+2Ѵ3<4+2x1,733
<=> 7,46<4+2Ѵ3<7,47
EXERCICE
V :
1) 4,25 ; 2,15 ; 0 ; 1,99
2,5
≤ x < 2,6
2) 4,26 ; 2,16 ; 0 ; 2
2,45 ≤ x < 2,55