PUISSANCE ET ENERGIE ELECTRIQUES

PUISSANCE ELECTRIQUE

Puissance nominale

     La puissance nominale d’un appareil est la puissance qu’il consomme lorsqu’il fonctionne normalement sous sa tension nominale ou tension d’usage.

          La puissance reçue par un dipôle est le produit de la tension à ses bornes par l’intensité du courant qui le traverse. Ainsi on a :

 P = U × I

P : puissance reçue par le dipôle en watt (W)

U : tension efficace aux bornes du dipôle en volt (V)

I : intensité efficace en ampère (A)

Exemple : Calculer l’intensité du courant électrique traversant une lampe halogène de puissance nominale P = 500 W alimentée sous une tension de 230V. On sait que P = U × I donc on en déduit que I = P /U = 500/ 230 = 2,17 A

Mesure de la puissance

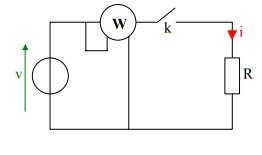
La puissance d’un appareil est donnée par un wattmètre.

ENERGIE ELECTRIQUE

Relation entre énergie et la tension électrique.

L'énergie électrique E transférée pendant une durée t à un appareil électrique récepteur fonctionnant sous une tension U et traversé par un courant I dépend :

• d'une part de la puissance P de l'appareil, exprimée en watt (W).

 • d'autre part, de la durée t de son fonctionnement. Ainsi l'énergie électrique transférée à un appareil électrique se calcule selon la formule :

 

E = P × t = U × I ×t

 

E : énergie électrique en J

P : puissance électrique en W

t : durée en s

U : tension en V

I : intensité en A

 Remarque :

L'unité internationale de l'énergie est le joule (J). On utilise aussi le wattheure (1Wh=3600J)

On obtient l'énergie en J uniquement si P est exprimée en watt et t en seconde. Pour obtenir l'énergie en kWh, il faut exprimer la puissance en kilowatt (kW) et la durée en heure (h).

 

Exemple :

Un chauffe-plats a une puissance de 50 Watt. Calculer l’énergie qu’il consomme en 15 minutes.

Sachant qu’un chauffe-plats a une puissance de 50 watts, l’énergie consommée en 15 min sera : P = 50 W, t = 15 min = 900 s

 E = P x t = 50 x 900 = 45 000 J soit 45 kJ

 

Loi de joule.

Énoncé de la loi de joule.

L’énergie électrique consommée dans un conducteur ohmique est égale au produit de la résistance du conducteur par le carré de l’intensité du courant et par la durée du passage du courant soit :          

 

W =R I2t.

 

Avec R(Ω), I(A), t(s), W(j).

 

Puissance consommée dans un conducteur par effet Joule

Soit un conducteur de résistance R, parcouru par un courant I. En régime permanent, la puissance consommée est :

 

P=RI2

 

 

Application de l’effet joule.

Il trouve son application dans plusieurs domaines :

-En électroménagers (fer à repasser, chauffe-eau, grille-pain)

-En industrie, les fours électriques.

-Dans les installations électriques (fusibles etc.)

 

Énergie électrique consommée dans une portion de circuit.

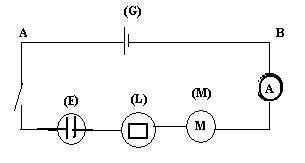
Considérons le circuit ci-dessous alimenté par un générateur de courant continu

Lorsque l’interrupteur est ouvert, on n’observe rien.

Dès que l’interrupteur est fermé, on constate que :

-L’aiguille de l’ampèremètre dévie, preuve que le courant circule dans le circuit.

-La lampe brille : elle transforme l’énergie électrique reçue en énergie calorifique (Wcal).

-Le moteur tourne : il transformé l’énergie électrique reçue en énergie mécanique (Wmec).

-Il y’a dégagement de gaz aux électrodes de l’électrolyseur, il transforme donc l’énergie électrique reçue en énergie chimique (Wch).

-La lampe le moteur et l’électrolyseur s’échauffent.

Lors du passage du courant électrique dans une portion de circuit, l’énergie électrique est donc transformée en énergie calorifique, chimique et mécanique d’où Wel = Wméc + Wch+Wcal.

 

 

EXERCICES

 

 

EXERCICE I:

1. Pendant combien de temps faut-il faire passer un courant de 2,5A dans un résistor de 50 Ω pour produire la quantité de chaleur nécessaire pour porter un litre d’eau de la température θ1=20 C a la température d’ébullition θ2=100 C ?

On donne ; chaleur massique de l’eau : 4190J.kg/C

2.Un conducteur, immergé dans un calorimètre de capacite calorifique μ=10 cal/C et contenant 100g de pétrole, est parcouru par un courant de 1 A pendant 3 mn ; sachant que la température du calorimètre et de son contenu s’élève de 3,6 C, calculer la résistance du conducteur.

On donne : Chaleur massique du pétrole :0,5 Cal/(g. C)  1 Cal=4,186 J

 

EXERCICE II:

 Un radiateur électrique porte les indications 230 V, 1500 W.

1. Quelle est l'intensité du courant qui le traverse lors d'un fonctionnement normal ?

2. Calculer l'énergie qu'il consomme en 24 heures.

3. Quel est son coût en 24 heures de fonctionnement continu si le kWh est facturé 50 F ?

 

EXERCICE III:

Un four alimenté sous une tension de 230 V continue est traversé par un courant I de 10 A.

1) Calculer la puissance électrique P de ce four.

2) Il fonctionne durant 1 min. Calculer l’énergie électrique consommée durant ce temps en joules puis en kWh.

3) Refaire les questions a et b pour une radio alimentée sous 230V et parcouru par un courant de 0,8A mais fonctionnant durant 6h.

 

EXERCICE IV :

Un moteur électrique, fonctionnant en régime permanent, développe une puissance mécanique de 1,5 KW et cède une quantité de chaleur de 1720 Kcal par minute. 1 Cal=4,19 J

On demande :

1-La puissance électrique totale consommée par le moteur ;

2-La ddp existant entre ses bornes, sachant que le courant de régime a une intensité de 13,5 A.

3-Le rendement du moteur (rapport de la puissance mécanique développée a la puissance électrique consommée)

4-L’energie électrique consommée en 8 h.

 

EXERCICE V:

Une installation électrique est alimentée sous une tension continue de 230 V. elle comporte les appareils suivants :

a) un fer à repasser de puissance électrique P1 = 800W.

b) un four de puissance électrique P2 = 1kW.

c) 10 lampes de puissance électrique valant chacune P = 60 W.

1) Tous ces appareils fonctionnent sous une tension continue de 230 V. comment doivent-ils être montés pour fonctionner en même temps ?

2) Calculer la puissance totale électrique que STEG doit fournir lorsque tous les appareils fonctionnent.

3) En déduire l’intensité du courant qui passe dans la ligne si tous les appareils fonctionnent.

 

EXERCICE VI:

Dans une installation domestique alimentée en 230 V, un électricien ne peut pas monter plus de 8 prises sur une ligne de 16 A.

1. Quelle est la puissance moyenne disponible sur chaque prise ?

2. Une salle de séjour dispose de 5 prises sur la même ligne. On branche un radiateur de 2000 W sur une des prises. Quelle est la puissance disponible sur les 4 autres prises ?

3. Outre l'appareil de chauffage, un téléviseur de 200 W est allumé ainsi qu'une lampe à halogène de 300 W. Que se passe-t-il si on branche un fer à repasser de 1500 W ?

4. Pourquoi impose-t-on une limite au nombre de prises ?

 

EXERCICE VII:

Un circuit électrique est formé des appareils suivants :

a) Un résistor constitue par un fil d’alliage de 2 m de long et de 0,4 mm de diamètre. Ce résistor est immergé dans un calorimètre en cuivre pesant 150 g et contenant 600 g d’eau.

b) Un électrolyseur a électrodes d’argent contenant une solution de nitrate d’argent.

c) Un électrolyseur a électrodes de platine contenant de l’eau acidulée par l’acide sulfurique et muni d’une éprouvette dans lequel se dégagent simultanément les gaz obtenus aux deux électrodes.

On fait passer dans le circuit un courant constant pendant 30 mn. Après passage du courant, la masse de l’une des électrodes de l’électrolyseur a nitrate d’argent a augmenté de 1,37 g et la température du calorimètre s’est élevée de 6,2  C.

1.    Calculer le volume dans les conditions normales de température et de pression, du gaz recueilli dans l’éprouvette du second électrolyseur.

2.    Calculer la valeur du résistor immergé dans le calorimètre. En déduire la résistivité de l’alliage utilisé.

Chaleur massique du cuivre :0,1 cal/g  C

Masse atomique de l’argent :108

 

 

CORRIGES

EXERCICE I:

1.) Q=mc Δθ : quantité de chaleur nécessaire

     W=RI2t : Energie dégagé par effet Joule

θ1=20+273=293

θs2=100+273=373     =>Δθ=80 K

Q=W =>mcΔθ = RI2t  =>t= mcΔθ/ RI2=1x4190x80/50x(2,5)2=1072,64 s soit 17mn53s

 

2. Q=(mc+μ)Δθ  en calories (1 Cal=4,186 J)

    W=RI2t     en joules        => R=( mc+μ)Δθ /I2t =(100x0,5+10)x4,186x3,6/(1)2x3x60=5Ω

 

EXERCICE II:

 

1. P=UI =>I=P/U=1500/230=6,52 A.

2. W=Pt=1500x24x3600=129 600 000 J

3. W=1500x24=36KWh

     Cout=36x50=1800 F

 

EXERCICE III:

1) P=UI=230x10=2300W

2) W=Pt=2300x60=138000J  or 1 Wh=3600J

W=138000/3600=38,33Wh soit 0,0383 KWh

3) P=UI=230x0.8=184 W

W=Pt=184x6x3600=3974400 J

W=Pt=184x6=1104Wh soit 1,104KWh

 

EXERCICE IV :

1-La puissance électrique totale consommée par le moteur ;

Pm=1,5 KW

Q=1720x4,190=7206,8 KJ soit 7206,8/60=120,11W=0,120KW

P=Pm +Q=1,5+0,120=1,62 KW.

2-La ddp existant entre ses bornes, sachant que le courant de régime a une intensité de 13,5 A.

P=UI => U=P/I=1620/13,5=120V

3-Le rendement du moteur (rapport de la puissance mécanique développée a la puissance électrique consommée)

r=1,5/1,62=0,93 ou 93%

4-L’energie électrique consommée en 8 h.

E=1,62x8=13 KW

 

EXERCICE V:

1) En parallèle

2) P=800+1000+60x10=2400W

3) I=P/U=2400/230=10,4 A.

 

EXERCICE VI:

1. Puissance moyenne disponible sur chaque prise

P=230x16=3680 W

2. Puissance disponible sur les 4 autres prises

3680-2000=1680 W

3. Lorsque on ajoute un fer à repasser on dépasse la puissance totale (1500+2500=4000W >3680W) =>Le disjoncteur ENEO saute et coupe la circulation du courant automatiquement radiateur

4. On impose une limite au nombre de prise pour ne pas dépasser la puissance fournie par ENEO

 

EXERCICE VII:

1.     

 

Q=mcΔθ=RI2t x4,190 =>R= mcΔθ/I2t=(600+150x0.1)x4,190x6,2/0,68x0,68x30x60=15976,47/832,32=19,19Ω

R=ρl/s =>ρ=Rs/l=19,19x3,14(0.4.10-3)2/4/2=1,2.10-6Ωm

Avez-vous un exercice a proposer?Cliquez-ici

Merci de votre visite
Laissez un commentaire